次に、定期検査時間による項が、車両寿命に関する項よりも十分小さく無視できるとした場合、つまり、$\lambda_{SM,DPF,lat}T_{lifetime}\gg\lambda_{SM,DPF,det}\tau_{SM}$の場合は、(63.1)は $$ M_{PMHF,M}\approx\lambda_{M,RF}+\frac{1}{2}\lambda_{M,DPF}\lambda_{SM,DPF,lat}T_{lifetime}\tag{64.1} $$ となり、PMHF規格第2式の

前のブログ 次のブログ

主機能フォールトによるVSGの場合のPMHF計算

前稿で目的の微小不稼働確率が求められたので、主機能フォールトに関するPMHFこと時間平均PUDを計算します。(61.5)に(62.3)を適用し、(60.6)及び(60.8)を適用すれば、PMHFの式は、 $$ M_{PMHF,M}=\overline{\varphi_{M}}\approx(1-K_{M,FMC,RF})\lambda_M\\ +\frac{1}{2}K_{M,FMC,RF}\lambda_M\lambda_{SM}[(1-K_{SM,FMC,MPF})T_{lifetime}+K_{SM,FMC,MPF}\tau_{SM}]\\ =\lambda_{M,RF}+\frac{1}{2}\lambda_{M,DPF}(\lambda_{SM,DPF,lat}T_{lifetime}+\lambda_{SM,DPF,det}\tau_{SM})\tag{63.1} $$ となり、これはPart10 8.3.3PMHF規格第1式の

と正確に一致します。ただし、条件に「安全機構に続いて指令ブロックの故障が引き起こされる可能性を考慮した」とあり、「SMのフォールトの後に主機能がフォールトする場合」と読めますが、以前PMHFの意味でも述べたように、(訳文ではなく)原文の誤りと思われます。その理由は、SMがフォールトしている場合は主機能フォールト抑止ができず、従って$\lambda_{RF}$とはならないからです。残余故障率が存在するためには、SMが稼働している必要があります。さらに、この場合、probabilityの訳語としては可能性よりも数学用語である確率のほうが適当です。

正しくは前稿までに見たように、OPR→SPF(安全機構のフォールトが無い状態で主機能フォールトの場合)及びLAT2→DPF(規格の条件どおり、安全機構に続く主機能のフォールトの場合)の2条件の和となります。つまり規格第1式は、安全機構のフォールトの有無を問わない、主機能フォールトによるVSG確率を意味しています。

順番については表で表した方が分かりやすいため、以下に4つのケースを示します。

規格第1式の条件である、「SMのフォールトの後に主機能がフォールトする場合」はCase 4のみを意味していますが、実際には数式は、主機能フォールトによるVSG確率、つまりCase 1とCase 4の場合の両方を意味しています。直観的にも理解されるように、 $$M_{PMHF,M}=\lambda_{M,RF}+\frac{1}{2}\lambda_{M,DPF}(\lambda_{SM,DPF,lat}T_{lifetime}+\lambda_{SM,DPF,det}\tau_{SM})\tag{63.1再掲}$$ の第1項がCase 1を、$\frac{1}{2}$以降の第2項がCase 4を表しています。

前のブログ 次のブログ

主機能M及び安全機構SMのペアについて、マルコフ状態遷移図を書いていきます。 まず、Mはアンリペアラブルであることを前提とし、SMはリペアラブルであることを前提とします。 しかし、MがフォールトしてもSMがそれをVSG(安全目標侵害)抑止している場合には、次のSMのフォールトは直ちにSG侵害となるため、一旦Mがフォールトとなった時点でSMはアンリペアラブルとなります。

まず、時刻$t$において、$\lbrace \mathrm{OPR:\ M\ up\ at\ }t\cap \mathrm{SM\ up\ at\ }t\rbrace$, $\lbrace \mathrm{SPF:\ M\ down\ at\ }t\cap\mathrm{VSG\ of\ M\ not\ preventable}\cap\mathrm{SM\ up\ at\ }t\rbrace$, $\lbrace \mathrm{LAT1:\ M\ down\ at\ }t\cap\mathrm{VSG\ of\ M\ preventable}\cap\mathrm{SM\ up\ at\ }t\rbrace$, $\lbrace \mathrm{LAT2:\ M\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\rbrace$, $\lbrace \mathrm{DPF:\ M\ down\ at\ }t\cap\mathrm{SM\ down\ at\ }t\rbrace$,の5状態があり、$t$から$t+dt$までの微小時間$dt$の間に遷移する微小確率PUDを求めます。

図のほうがわかりやすいので、以下にマルコフ状態遷移図を示します。

マルコフ状態遷移図でのOPR→SPF

図より微小不稼働確率をPUDで表すと、 $$ q_{M,SPF}(t)dt=\Pr\{\mathrm{OPR\ at\ }t\cap\mathrm{M\ down\ in\ }(t, t+dt]\cap\mathrm{VSG\ of\ M\ not\ preventable}\} \\ =\Pr\{\mathrm{M\ up\ at\ }t\cap\text{SM up at }t\cap\mathrm{M\ down\ in\ }(t, t+dt]\cap\mathrm{VSG\ of\ M\ not\ preventable}\} \\ =\Pr\{\mathrm{VSG\ of\ M\ not\ preventable}\}\Pr\{\mathrm{M\ fails\ in}(t, t+dt]\ |\ \mathrm{M\ up\ at\ }t\}\Pr\{\mathrm{M\ up\ at\ }t\}\Pr\{\text{SM up at }t\}\\ =(1-K_{M,FMC,RF})A_{SM}(t)R_{M}(t)\lambda_{M}dt=(1-K_{M,FMC,RF})A_{SM}(t)f_{M}(t)dt\tag{62.1} $$

マルコフ状態遷移図でのLAT2→DPF

図より微小不稼働確率をPUDで表すと、 $$ q_{M,DPF}(t)dt=\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{M\ down\ in\ }(t, t+dt]\}\\ =\Pr\{\mathrm{SM\ down\ at\ }t\cap\mathrm{M\ up\ at\ }t\cap\mathrm{M\ down\ in\ }(t, t+dt]\}\\ =\Pr\{\mathrm{SM\ down\ at\ }t\rbrace\Pr\{\mathrm{M\ fails\ in}(t, t+dt]\ |\ \mathrm{M\ up\ at\ }t\}\Pr\{\mathrm{M\ up\ at\ }t\}\\ =Q_{SM}(t)R_{M}(t)\lambda_{M}dt=Q_{SM}(t)f_{M}(t)dt\tag{62.2} $$

主機能フォールトによるVSG

以上から(62.1)と(62.2)を加えれば、MによりSPFもしくはDPFとなる場合の微小遷移確率が求められ、 $$ q_{M}(t)dt=q_{M,SPF}(t)dt+q_{M,DPF}(t)dt=\left[1-K_{M,FMC,RF}A_{SM}(t)\right]f_{M}(t)dt\\ =\img[-1.35em]{/images/withinseminar.png} ただしu\equiv t\bmod\tau_{SM}\tag{62.3}$$ となります。

前のブログ 次のブログ

PUD(Point Unavailablity Density)の定義からご紹介します。とはいえ、これは弊社の造語であり本ブログと論文だけで通用するものです。このPUDは不稼働密度とでも訳すべきものであり、以下に定義を示します。

PUD:

PUD、すなわち不稼働密度$q_{item}(t)$は、前々回ご紹介したポイントアンナベイラビリティ(PUA)の時間微分で、以下の微小不稼働確率を$dt$で割ったものです。$q_{item}(t)$の式にすると$\lim_{dt \to 0}$が出てくるため、形式的に両辺に$dt$をかけ微小不稼働確率としています。 $$q_{item}(t)dt\equiv(\frac{dQ_{item}(t)}{dt})dt=\img[-1.35em]{/images/withinseminar.png}\tag{61.1}$$

PMHFは、修理系アイテムの車両寿命間のダウン確率の時間平均であることから、ここで示すアイテムの平均PUDと考えられます。このことは規格Part5には以下のように書かれています。

「アイテムの作動寿命間の毎時平均確率」とは舌足らずであり、何の確率かが書かれていません。その前に「ランダムハードウェア故障」とあるため文脈から故障確率であると読み取れますが、修理系の場合は厳密には故障確率ではなく、故障したものが修理される事象を含めたダウン確率です。

従って、PMHFを求めるにはまず微小不稼働確率に着目して確率微分方程式を立て、それを0から車両寿命$T_{lifetime}$まで積分し、$T_{lifetime}$で割って平均PUDを算出する流れで求めます。

前のブログ 次のブログ

※この記事は2018年に書かれたものであり、基本的には変わりませんが最近の記事で詳細計算を行っています。

SMのアンナベイラビリティ(不稼働率、PUA)$Q_{SM}(t)$の導出

以前PMHF式を以下で導出しました。 https://fs-micro.com/post/show/id/10.html

ここでは再度PMHFの式を導出して行きますが、事前準備がいくつか必要になりますので、まず、修理系のアンナベイラビリティの公式を導きます。

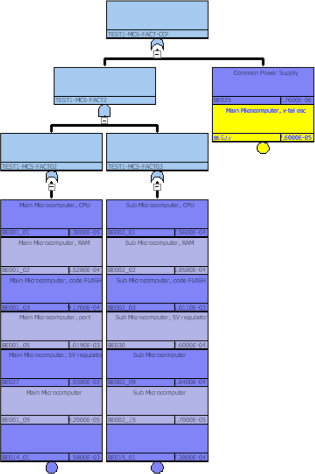
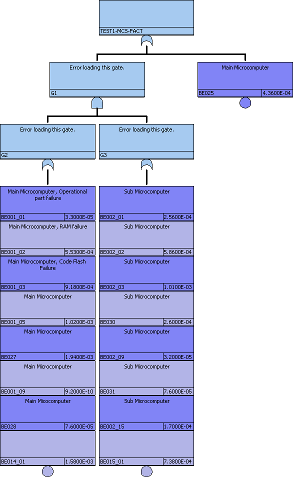
まず、修理系とは何かを説明します。ISO 26262規格には修理の問題についてはっきり書いていませんが、1st SMが修理系となります。1st SMとは、1st order SMとも呼ばれ、主機能のSG侵害(安全目標侵害=VSG)を防止するためのSMです。一方で、主機能は非修理系です。

1st SMは、2nd SMにより定期的に検査され、故障だと判明した場合は直ちに修理されます。2nd SMとは2nd order SMとも呼ばれ、エレメントがレイテントフォールトとなるのを防止する安全機構です。規格にもあるとおり、修理周期は「検査周期($\tau_{SM}$)＋ドライバーが修理工場へ運転して行く時間＋修理にかかる時間」です。従って、修理周期＝2nd SMの検査周期とみなせます。

規格にははっきり書かれていませんが、検査により故障と判明した部分については、修理され新品同様(as good as new)と見なされます。この検査による故障検出割合が重要であり、Part 10では定数値$K_{FMC,MPF}$で表されます。故障したうちの検出部分なので(59.1)のように条件付き確率と考えがちですが、 $$K_{FMC,MPF}=\Pr\lbrace \text{detectable}\ |\ \text{failed at }t \rbrace\tag{59.1}$$ 故障検出能力は確率的に決まるものではなく、アーキテクチャ的に決まるものだと考えるため、もともとの検出部分の故障について検出可能とします。 $$K_{FMC,MPF}=\Pr\lbrace \text{detectable} \rbrace\tag{59.2}$$ 検出された故障は全て修理されるものとします。 $$\Pr\lbrace \text{repaired}\ |\ \text{detected at }t\rbrace=1\tag{59.3}$$

次にアンナベイラビリティ$Q_{SM}(t)$とは、省略せずに言うとポイントアンナベイラビリティ(PUA)であり、修理系の不稼働率です。 確率の式で表せば、

PUA: $$Q_{SM}(t):=\Pr \lbrace \text{(repairable)SM down at }t \rbrace\tag{59.4}$$ のように、時刻$t$において不稼働である確率を意味します。

一方で、アベイラビリティの式は参考ページまたはBirolini教授の教科書を参照すれば、 $$ A(t):=R(t)+\int_0^t m(x)R(t-x)dx\tag{59.5} $$ であり、ここで、$A(t)$は時刻tにおけるポイントアベイラビリティ、$R(t)$は時刻tにおけるリライアビリティ(信頼度)、$m(t)$は時刻tにおけるリニューアル密度(修理密度)です。規格の特徴として、修理周期は教科書一般にあるように指数関数分布はとらず、定期的に$\tau_{SM}$毎に行われるため、以下の式が成立します。 $$A_{SM}(t)=R_{SM}(t)+K_{SM,FMC,MPF}F_{SM}(\tau_{SM})\sum_{i=0}^{n-1}R_{SM}(t-i\tau_{SM})\tag{59.6}$$

修理分$K_{SM,FMC,MPF}F_{SM}(\tau_{SM})$が時刻$t$の関数でないのは、検出能力$K_{FMC,MPF}$は一定で、かつ毎回の故障確率も一定で、検出した分は全て修理されるため、修理分が一定となるためです。 従って、SMのポイントアベイラビリティ式は以下のようになります。 $$A_{SM}(t)dt=\img[-1.35em]{/images/withinseminar.png}\tag{59.7}$$

これを1から引けば、SMのポイントアンアベイラビリティ(PUA)は以下のように求められます。

PUA: $$Q_{SM}(t)dt=\left[1-A_{SM}(t)\right]dt=\img[-1.35em]{/images/withinseminar.png}\tag{59.8}$$

(59.8)の両辺を時刻$t$で微分すれば、微分可能な$t$におけるPUD(Point Unavailability Density)が求められます。

PUD: $$q_{SM}(t)dt:=(\frac{dQ_{SM}(t)}{dt})dt=\img[-1.35em]{/images/withinseminar.png},\\ \ t\notin\{\tau_i=i\tau; i=1,2,...,n\}\tag{59.9}$$

※ここでの議論において、次に示すような形式的な記法を用いています。例えば、 $$f(t)=\lim_{dt\to +0}\frac{F(t+dt)-F(t)}{dt}=\frac{dF(t)}{dt}$$ と書くところを$dt$が無限小であることを前提として、 $$f(t)dt=dF(t)$$ としています。確率密度関数$f(t)$を求めるよりも、微小確率$f(t)dt$を求めるほうが、次での積分の記述が容易になるためです。

なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。

前のブログ 次のブログ

共通原因故障(CCF)

前稿では冗長制御方式を取り上げて、メインマイコンとサブマイコンがお互いに主機能とSMの関係になっており、SPFを防止していることを説明しました。共通原因故障(Common Cause Failure, CCF)が無い理想的な場合にはこれが成立します。一方、メインマイコンとサブマイコンにCCFを持つ場合にはどうなるか、MCSを取得してみましょう。

CCFの例

メインマイコンとサブマイコンに共通の発振回路からクロックを供給している場合はどうでしょうか？ メインマイコン発信回路の故障をBE028、サブマイコン発振回路の故障をBE031としていたもとのツリーを変更してBE031をBE028に置き換えてみます。こうすると冗長系の両側に共通の故障原因BE028を持つことになり、MCSを取得すると以下のようにANDの下だったものが上位のORに接続され、SPFの原因となります(図29.1)。

図29.2はブール代数の分配則であり、これにより上記論理変換が行われます。

これは何を意味するかというと、共通の電源、クロック源、あるいは共通の型番を持つと、単一のランダムハードウェア故障ないしはシステマティック故障により、メインマイコンとサブマイコンのお互いの安全機構の構造が崩れて、単一原因により安全目標が侵害されるとことになり、重要な故障となることを意味します。

ISO26262はこのCCFを定量的に計算する手段を規定していないため、ISO26262のベース規格であるIEC61508に記述されているCCFのβファクタを援用することになります。また、ISO26262の発展規格であるISO19451において、従属故障分析(DFA, Dependent Failure Analysis)として詳述されていますので、ご参照ください。

前のブログ 次のブログ

因数分解

前稿のMCSにおいて因数分解を行います。このステップは必須のステップではありません。論理的には前のツリーと等価なツリーなのですが、冗長構成となっていることをひとめで明らかにするために因数分解を行います。上記のMCS論理式を因数分解したものを以下のFTに示します。因数分解はAND-OR形式をOR-AND形式に変換するものですが、残念ながら自動的には困難であるため、人力で行います。

論理等価なのでMCSは上記MCSと同じです。メインマイコン各部(8箇所)の故障とサブマイコン各部(8箇所)の故障が互いに主機能・安全機構の関係となりSPFを防止しており、共通部分の回路のみがSPFとなっていることがひとめでわかります。MCの数は前と同じく8×8+1=65項となります。

ISO26262の目的は安全に関する論証なので、このようにアセッサー等の第三者が見てわかりやすいドキュメントを生成することが重要です。マイコンやLSIのように比較的故障率の大な部品を使用する際に、マイコン単体でASIL-Dを達成するのは困難ですが、このような冗長構成をとればSPF/RFが冗長部分で微小となるため、ASIL-D対応が可能となります。

前のブログ 次のブログ

実際の例

システムFTAの実例をご紹介します。これはあるECUの安全分析を実施したもので、メインマイコンとサブマイコンによる冗長制御を行っているECUの例です。電源回路は共通で、共通の信号が両マイコンに入力され、両マイコンの出力が揃って初めて動作するという回路構成となっています。主機能としてはマイコンはひとつで成立するのですが、ECUがASIL-D対応をする必要があるため、冗長構成をとり故障率を低減しています。

システムFTAと称する理由は、基事象が部品の故障モードではなく、エレメントの故障モードとなっているためです。

トップ事象を侵害する分析は、このように一般的に非常に複雑になり、マイコンの故障が複数個所に出てくることになります。以下はFTの図です。

MCSの導出

この例のMCSを取得したものが以下の図です。SAPHIREにより155個の積項(ミニマルカット=MC)が得られました。カラムは順番に、その事象の「連番」、「ケース」、「確率」、「確率のパーセント表記」、「ミニマルカット」です。

3次以上の次数項の省略

次にSAPHIREの分析の際に、3次以上の積項を省略したMCSを取得してみます。3次以上の積項を省略する理由は、ISO26262において3点故障はセーフフォルトとして良いとあるためであり、3次以上の積項は一般的に確率的に非常に小さいので省略可能なためです。

これを行うにはSAPHIREにおいて、Fault Treeを選択しSolveコマンドを実行する際に、Sizeに2を設定します。すると155個得られた積項が65個と減少します。以下のMCSの論理式を確認すると1次と2次の積項のみであることがわかります。今回はTOP事象の侵害確率は、155項の積算でも65項の積算でも2.218E-5と変わりませんでした。これからも3次以上の積項を省略することが可能と言えます。

これを論理式として出力し、FTL(Fault Tree Language)に(手で)変換してからSAPHIREに取り込むと、SAPHIREがツリーを構成してくれます。その図を以下に示します。

前のブログ 次のブログ

MCSのFault Tree

SAPHIREではMCSの論理式は出力してくれるのですが、残念ながらFault Tree図(FT図)は構成されません。そこで、論理式からのインポートを行います。まず論理式は図26.2のように出力されるので、それをFTL(Fault Tree Language)に変換しますが、変換したものを以下に示します。

WARWICKFTA, TOP-MCS =
TOP-MCS OR TOP0 TOP1
TOP0 AND E1 E3 E4
TOP1 AND E2 E3 E4

その後、SAPHIREのインポート機能により取り込み、FT図を作成したものが、図27.1となります。

前のブログ 次のブログ

論理圧縮の実際

前回ご紹介した、英国Warwick大学のFTに対して、SAPHIREでTOP事象侵害確率を求めてみます。 FTのイベントに対して、$A=e_1$、$B=e_2$、$C=e_3$、$D=e_4$と置き直して、FTA(5)の表24.1のイベントの故障率に基づけば、

これらに基づきSAPHIREでFTを構成すると図26-1のようになります。

SAPHIREによりMCSを求め、TOP事象侵害確率を求めると以下の表のようになります。車両寿命を$10^5$時間とすれば、平均的な故障率は$8.186\cdot 10^{-6}[FIT]$となります。

MCSは同じく{{A, C, D}, {B, C, D}}と求められます。

前のブログ 次のブログ