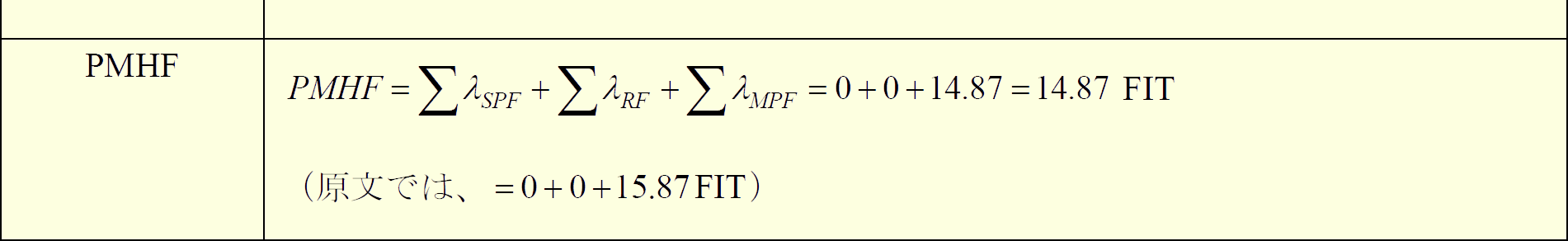表328.1はRAMS 2021正式採択までのマイルストーンです。論文執筆は完了しました。

表328.1　RAMS 2021へのマイルストーン

年月日	マイルストーン	状態
2020/7/3	学会出席確認	済
2020/8/5	論文、プレゼン投稿締め切り(名前、所属無し版)	済
2020/9/7→2020/9/16	第1回査読コメント受領	済
2020/10/2→2020/9/27	改訂版論文、プレゼン投稿締め切り(名前、所属無し版)	済
2020/10/6→2020/9/21	学会出席登録締め切り	済
2020/10/13→2020/10/19	最終査読コメント受領	済
2020/10/27→2020/10/26	最終論文、プレゼン投稿締め切り(名前、所属有り版)	済

---

前のブログ 次のブログ

こんどはYoutubeでおかしな表現を見つけました。図327.1に当該部分を引用します。

図327.1 あるYoutube動画中のPMHFの説明

• SPFMの説明にはSPFをカバーすると書かれています。SPFは広義ではRFを含むこともあり、広義と教義があるので、広義だとすれば問題ありません。
• LFMの説明にはなぜかLFMと書かれていません。説明はLFをカバーすると書かれており、OKです。カバレージの意味もあるのかもしれませんが。
• PMHFの説明には、残余ハードウエアフォールトをカバーすると書かれています。通常はRFのことなので、ここにおいて最初のSPFの説明にRFが含まれなかった、つまり狭義のSPFだったことがわかります。

以上から、SPFMとPMHFの説明は誤りです。ただしくは、SPFMはSPF及びRFの両方のカバレージを意味します。さらに、PMHFはアイテムの車両寿命におけるダウン確率の時間平均を意味します。

この動画はあまり良くなく、FMEDAでSPFM/LFM/PMHFを計算すると言っています。原理的にFMEDAではPMHFを正しく計算するのは困難です。ワーストケースと思えば良いかもしれません。それにしても規格式を正しく実装しているかどうかが不明です。この動画は、自社のツールを使えば、ブラックボックスでアーキテクチャメトリクスが計算できると言っているにすぎません。

Youtubeで調べましたが、正しいPMHFの計算法を紹介している動画は見つかりませんでした。

---

前のブログ 次のブログ

参照論文の調査

PMHF式に誤りのある「平成26年度 電子部品信頼性調査研究委員会 研究成果報告書」は2015年3月発行です。著者に連絡を取ったところ、論文$\dagger$からの引用だとのことでした。これは2014年発行なので、この論文$\dagger$が元凶であり、ブログで取り上げた日本人の資料である、この資料とこの資料に影響を与えたようです。IEEE発行の査読付き論文なのでそれなりに信用性があり、誤りが広まってしまうのかもしれませんが、非常に遺憾なことです。

もっとも、査読済み論文だからと言って、検証もしないで盲目的に引用する態度にも同様に問題があると考えます。

図326.1に当該部分を引用します。良くみると、上記報告書が引用したといいながら、DPF部分はlatentのみとなっています。従って、上記報告書と論文$\dagger$では少々異なります。

図326.1 ある論文中のPMHF式 この資料と、参考にした元論文の例では1st SMは存在しても2nd SMの概念が全く書かれていないので$\lambda_\text{MPF}$と$\lambda_\text{MPF,lat}$は一致するのでしょう。

IEC 61508との比較

また、図326.1の説明には、

ISO 26262にはSPFMやLFMと異なりPMHF式が出ていないためIEC 61508を参照する

と書かれていますが、実際はPart 10に式が記載されています。さらにIEC 61508にはPMHFはありません。近い概念としてはPFH(Probability of Failure per Hour)があります。Exidaの資料によればPFHは(326.1)式で表されます。 $$ PFH=\lambda_\text{DU}\tag{326.1} $$

ただし、これは1oo1の式だと思われます。少なくともDPFは、主機能と安全機構の双方がフォールトしたときの故障であるため、1oo2の式のほうがベターです。

しかしながら、ISO 26262はIEC 61508に基づいているといいながら、PMHF結果式はISO 26262独特のものであるため、1oo2としても式は一致しません。具体的には、ISO 26262はIEC 61508と異なり定期検査及び修理が前提となっています。

IEC 61508で学んだ多くの研究者が同じ誤りを起こしています。論文を見るとすぐ分かります。それは、ISO 26262にはDD, DUという用語は無いにもかかわらず、そのような用語を使用しているからです。そのような概念を表すものはKパラメータと呼ばれる診断率DCであり、 $$ \lambda_{DD}=K_\text{RF}\lambda_\text{IF}, \lambda_{DU} =(1-K_\text{RF})\lambda_\text{IF} $$ と表現しなければいけません。IEC 61508を過度に適用することは、上記の誤りにつながります。正しくはあくまでISO 26262の上で考えなくてはなりません。特にIEC 61508にはDPFの概念が無いため注意が必要です。

---

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

---

前のブログ 次のブログ

「電子部品信頼性調査研究委員会 研究成果報告書」中のPMHF式

この誤りはどこかで見たと思ったら、財団法人日本電子部品信頼性センター発行の「平成26年度 電子部品信頼性調査研究委員会 研究成果報告書」の33ページにも、同じような式が書かれていたので、図325.1に引用します。

図325.1 ある資料中のPMHF式

前稿のMPFはLF($=\lambda_\text{MPF,lat}$)のみを加えていましたが、この式ではMPF全体となっており、誤りはより悪化しています。これはtypoではなく、図325.1中にも「全体から安全フォールトを除いたもの」とあり、図324.1を参照すれば、SPF/RFに加えMPF全体と考えているようです。ところが、MPFにはlatentとdetected/percievedがあり、後者は安全と考えられるので、より誤り度合いが大きいのです。

前稿でも述べたように、LFは単独ではVSGとならないので、他のフォールトとのDPFとして計算する必要があります。DPF確率は、SMのレイテント確率とIFのフォールト確率の積になります。

図325.2 ある資料中のPMHF計算

本来DPFは、このように2つのフォールト確率から成る確率事象であるため、その確率は非常に小さくなるはずです。具体的には故障率のオーダーが$10^{-9}$、車両寿命が$10^{5}$とすれば、かけ合わせると1万分の一のオーダーです。ところが、図325.2ではDPFが100%になっており、一見して誤りと判定できます。

もっとも$\lambda_\text{SPF/RF}$がゼロならDPF項は必ず100%ですが、そもそも$\lambda_\text{SPF/RF}$がゼロという点が信じられません。その理由はDPF項は経験的に3%未満だからです。

---

前のブログ 次のブログ

「自動車の機能安全と部品安全」中のPMHF式

昆虫採集よろしく、業界内での事例収集を実施中です。アーキテクチャメトリクス(SPFMとLFMの総称)及びPMHFについて、「自動車の機能安全と部品安全ーISO 26262の概要ー」の資料(安部秀二、パナソニック)を見つけました。

その中での、上記メトリクスの計算方法を紹介します。

図324.1 ある資料のメトリクス算出例

この資料によれば、SPFMは資料の$\alpha$、$\beta$、$\delta$を用いて $$ M_\text{SPFM}=1-\frac{\beta}{\alpha}=1-\frac{\sum\left(\lambda_\text{SPF}+\lambda_\text{RF}\right)}{\sum\lambda} \tag{324.1} $$ と表され、LFMは、 $$ M_\text{LFM}=1-\frac{\delta}{\alpha-\beta}=1-\frac{\sum\lambda_\text{DPF,lat}}{\sum\left(\lambda-\lambda_\text{SPF}-\lambda_\text{RF}\right)} \tag{324.2} $$ と表されます。

それぞれ、(324.1)を図122.1のSPFMの規格式、(324.2)を図123.1のLFMの規格式と比較すれば、一致していることがわかります。ここまでは問題ありません。

一方、$M_\text{PMHF}$は、 $$ M_\text{PMHF}=\beta+\delta=\lambda_\text{SPF}+\lambda_\text{RF}+\lambda_\text{DPF,lat} \tag{324.3} $$ (324.3)は誤りです。LFは単一ではVSGを引き起こさないため、アイテムのVSG確率としては、$\img[-0.9em]{/images/withinseminar.png}$ とする必要があります。

これは2015年の資料ですが、いったい(324.3)はどこから来たのでしょうか?

---

前のブログ 次のブログ

弊社では、定量FTAを用いてPMHFを見積もる論文を、RAMS 2021に提出済みです。さて、PMHFが業界でどのように見積もられているかを調べたところ、この資料を見つけました。

図323.1 ある資料のFT構成法

図323.1は少々複雑なので、思想を曲げない範囲で簡略化します。まず、SPFはDC=0の時のRFであるため、SPF/RFをひとまとめにし、 $$ \lambda_\text{IF,RF}=(\lambda_\text{G}+\lambda_\text{K}+\lambda_\text{B}+\lambda_\text{F})(1-DC)=(1-DC)\lambda_\text{IF}\tag{323.1} $$ (323.1)はRFの式そのものであり、OKです。

次に、DPF1ですが、これはSM1の不信頼度がかかっていることから、SM1が先にLFとなり、続いてIFがフォールトしVSGとなるDPFだと考えられます。DPF1は、 $$ \lambda_\text{DPF1}=\lambda_\text{IF}\cdot DC\cdot\frac{1}{2}\lambda_\text{SM1}T=\frac{1}{2}DC\lambda_\text{IF}\lambda_\text{SM1}T, ただし、\lambda_\text{SM1}=\lambda_\text{C}+\lambda_\text{I}+\lambda_\text{M}\tag{323.2} $$ Fault Tree中は故障率で書かれているので、少々心配になりますが(このような誤りが多々あるので)、きちんと$T$をかけて単位を[1/H]としているので、(323.2)もOKです。

最後にDPF2は、IFの不信頼度がかかっていることから、IFが先にLFとなり、続いてSM1がフォールトしVSGとなるDPFだと考えられます。DPF2は、 $$ \lambda_\text{DPF2}=\lambda_\text{SM1}\cdot\frac{1}{2}\lambda_\text{IF}T=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM1}T\tag{323.3} $$ 残念ながら(323.3)は誤りです。以下に列挙すると、誤りは、

1. まず、IFとSM1の両方がリペアラブルではないことです。もっともこれは規格式も誤っているので見逃します。

2. 次に、$\lambda_\text{DPF2}$において、$\lambda_\text{IF}$に$DC$がかかっていないことが誤りです。なぜなら$\lambda_\text{IF}$のうち、$1-DC$分、つまり$(1-DC)\lambda_\text{IF}$がRFとなり、残りの$DC$分、つまり$DC\lambda_\text{IF}$がLFとなるためです。従って、正しくは $$ \lambda_\text{DPF2}=\lambda_\text{SM1}\cdot\frac{1}{2}\lambda_\text{IF}DC T=\frac{1}{2}DC\lambda_\text{IF}\lambda_\text{SM1}T $$ ところが、$\lambda_\text{DPF1}$と比較すればわかるように$\lambda_\text{DPF1}\equiv\lambda_\text{DPF2}$なので、実は別のツリーとする必要はありません。

3. さらに、2nd SMのカバレージであるDC2が全く考慮されていないことも問題です。ただし、DC2=0のワーストケースの評価であれば問題ありません。

従って、大きな誤りは2番目の項目となります。とはいえ、ほとんど全ての論文において定量FTAでDPFまで計算しているものが無いことから、本資料は良いほうだと言えます。

結論として、上記2.の修正を行えば、「故障順序によらないPMHF式」(105.6)と一致します。ここで(105.6)を再掲すれば、 $$ M_{\mathrm{PMHF}}= (1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}+ K_{\mathrm{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}\\ \tag{105.6} $$ 次に、2nd SMが不在というワーストケースを仮定して$K_{\mathrm{SM,MPF}}=0$とし、$K_{\mathrm{IF,RF}}=DC$と置きなおせば、 $$ M_{\mathrm{PMHF}}=(1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}+ K_{\mathrm{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}T_\text{lifetime}\\ =(1-DC)\lambda_{\mathrm{IF}}+ DC\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}T_\text{lifetime}\\ \tag{323.4} $$ (323.1)~(323.3)を全て加えると、(323.4)と一致することがわかります。

---

前のブログ 次のブログ

表322.1はRAMS 2021正式採択までのマイルストーンであり、今後適宜更新します。

表322.1　RAMS 2021へのマイルストーン

年月日	マイルストーン	状態
2020/7/3	学会出席確認	済
2020/8/5	論文、プレゼン投稿締め切り(名前、所属無し版)	済
2020/9/7→2020/9/16	第1回査読コメント受領	済
2020/10/2→2020/9/27	改訂版論文、プレゼン投稿締め切り(名前、所属無し版)	済
2020/10/6→2020/9/21	学会出席登録締め切り	済
2020/10/13→2020/10/19	最終査読コメント受領
2020/10/27→2020/10/26	最終論文、プレゼン投稿締め切り(名前、所属有り版)

---

前のブログ 次のブログ