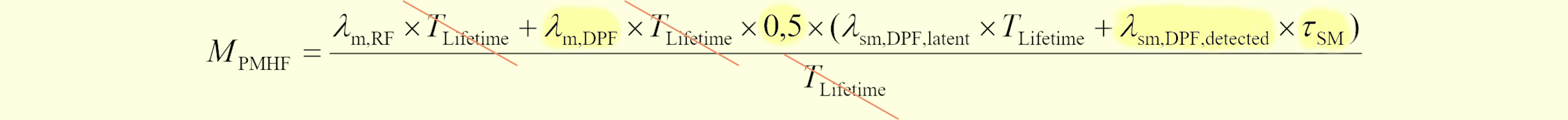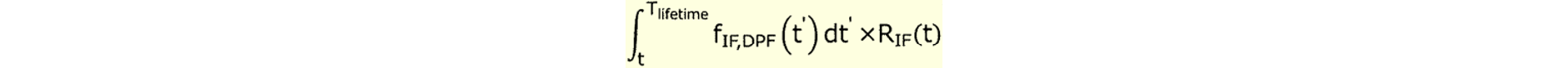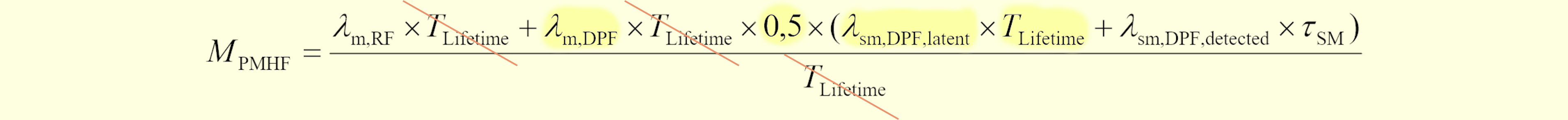パターン2
続いてパターン2です。前稿の続きです。
- Pattern 2: SM1⇒IFの順にフォールトが発生し、SM1のフォールトは、SM2によって緩和され通知される。フォールトの暴露時間は、運転手が修理のために車両を持ち込むのに必要な予想される時間。
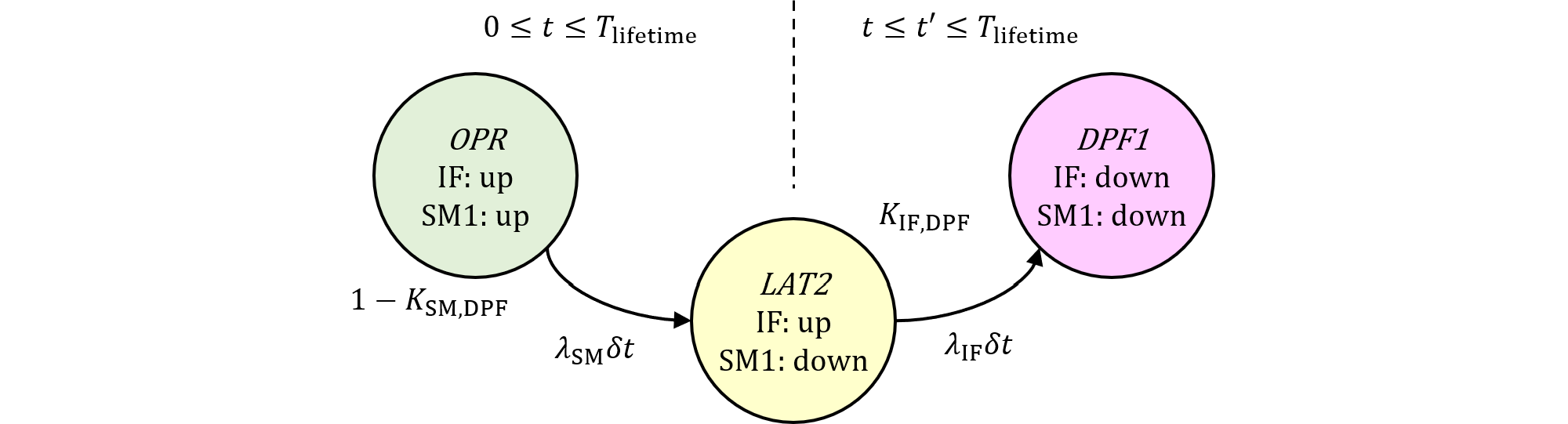
これはSM1のフォールトが2nd SMの定期周期$T_\text{service}$により検査され、検出割合は$K_\text{SM,DPF}$でありその全量が修理されるパターンです。時刻パラメータ$t$が最初のSMのフォールトが起きた時刻、$t'$がVSGとなる2つ目のIFのフォールトが起きた時刻とします。
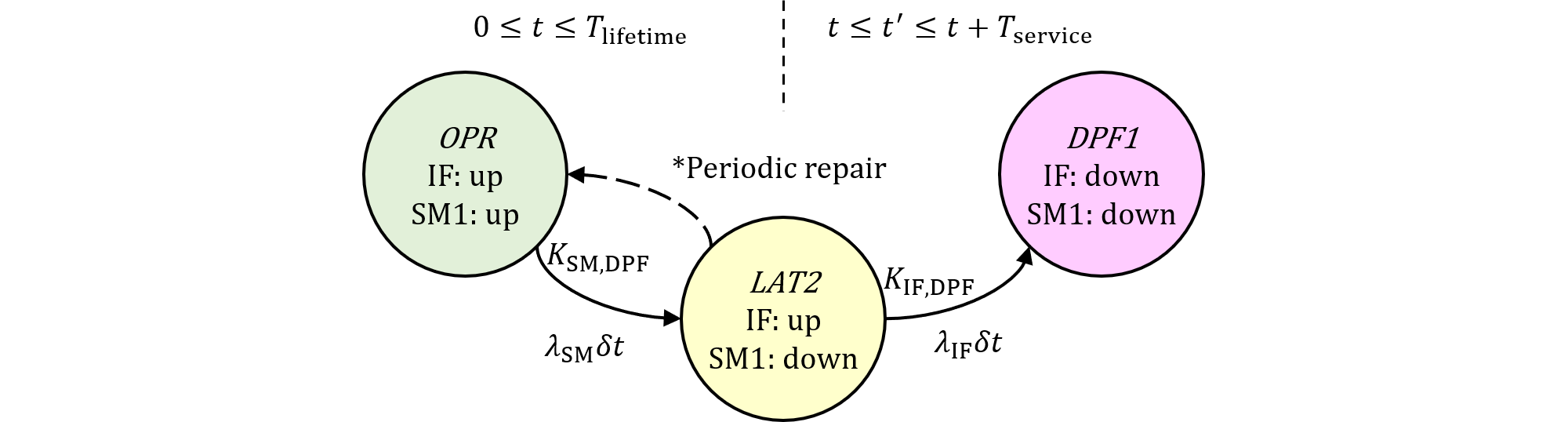 図472.1 2nd editionパターン2マルコフ図
図472.1 2nd editionパターン2マルコフ図
まずIFについては前稿と同様です。IFの$LAT2S$での状態確率は、
$$
\Pr\{\text{IF in }LAT2S\}=\Pr\{\text{IF up at }t'\cap\text{VSG of IF prevented}\}=K_\text{IF,DPF}R_\text{IF}(t')
\tag{472.1}
$$
$LAT2S$から$DPF1S$への微小時間での遷移確率は、IFがDPFする場合であり、
$$
\Pr\{\text{IF down in }(t', t'+dt']\ |\ \text{IF up at }t'\cap\text{VSG of IF prevented}\}=\lambda_\text{IF}dt'
\tag{472.2}
$$
規格のとおりIFの確率を求めるには、IFは時刻$0$から$t'$まではフォールトせず(解説書の$t$は誤り)、かつ、IFに関するDPF確率密度を$t$から$t+T_\text{service}$まで$t'$について積分し、$t$で表します。
実はここに誤りがあり、期間を$t$から$t+T_\text{service}$とすると、SM1⇒IFの順のフォールトだけでなく、その逆順のフォールトも含まれます。
その理由は、パターン2は検出可能部分のSM1のフォールトなので、期間間隔$T_\text{service}$内にDPF、すなわち1つめのSM1のフォールトと2つめのIFのフォールトが両方共起きる必要があります。図472.1の$OPRS$から$LAT2S$、さらに$LAT2S$から$DPFS$までを1回の間隔$T_\text{service}$内で遷移する必要があります。
また、その順序もSM1⇒IFと決まっています。SM1のフォールトが起きた時のIFのフォールト生起確率という条件付き確率であれば良いのですが、そうではなくIFとSM1のフォールト確率は独立とするならば、期間間隔$T_\text{service}$を考えるとSM1⇒IFだけでなくIF⇒SM1も含まれてしまいます。従って、半分の期間間隔$\frac{1}{2}T_\text{service}$を考えるか、または期間間隔$T_\text{service}$での確率を求めて0.5をかけるのが正解です。従って後者をとれば、
$$
\Pr\{\text{IF fails }\bbox[#ffccff,2pt]{\text{last}}\text{ in }[t', t'+T_\text{service}])=\frac{1}{2}\Pr\{\text{IF down in }[t', t'+T_\text{service}])
$$
従って、(472.1)、(472.2)から、IFの後故障確率の$t$の時の値は
$$
\require{cancel}
\frac{1}{2}K_\text{IF,DPF}\int_t^{t+T_\text{service}}R_\text{IF}(t')\lambda_\text{IF}dt'=\frac{1}{2}K_\text{IF,DPF}\int_t^{t+T_\text{service}}f_\text{IF}(t')dt'\\
=\frac{1}{2}K_\text{IF,DPF}\left[F_\text{IF}(t')\right]^{t+T_\text{service}}_t=\frac{1}{2}K_\text{IF,DPF}\left[F_\text{IF}(t+T_\text{service})-F_\text{IF}(t)\right]\\
\approx\frac{1}{2}K_\text{IF,DPF}\left[\lambda_\text{IF}(\bcancel{t}+T_\text{service}\bcancel{-t})\right]=\frac{1}{2}K_\text{IF,DPF}\lambda_\text{IF}T_\text{service}
\tag{472.3}
$$
次に、SMの$OPRS$での状態確率は、$u\equiv t\bmod T_\text{service}$とすれば、
$$
\Pr\{\text{SM in }OPRS\}=\Pr\{\text{SM is up at }u\}=R_\text{SM}(u)
\tag{472.4}
$$
$OPRS$から$LAT2S$への微小時間での遷移確率は、SMがフォールトする場合であり、
$$
\Pr\{\text{SM down in }(u, u+du]\ |\ \text{SM is up at }u\}=K_\text{SM,DPF}\lambda_\text{SM}du
\tag{472.5}
$$
次にIFとSMのフォールトは独立事象であるため、IFの確率とSMの確率の積をDPF確率として、$0$から$T_\text{lifetime}$まで積分するがSMの確率は周期$T_\text{service}$でゼロとなるため、$T_\text{lifetime}$中には$n\equiv\frac{T_\text{lifetime}}{T_\text{service}}$回存在します。従って(472.3)~(472.5)を用いて、
$$
\require{cancel}
M_\text{PMHF,P2}\approx\frac{1}{\bcancel{T_\text{lifetime}}}\frac{\bcancel{T_\text{lifetime}}}{\bcancel{T_\text{service}}}\int_0^{T_\text{service}}K_\text{SM,DPF}R_\text{SM}(u)\lambda_\text{SM}\frac{1}{2}K_\text{IF,DPF}\lambda_\text{IF}\bcancel{T_\text{service}}du\\
=\frac{1}{2}K_\text{SM,DPF}K_\text{IF,DPF}\lambda_\text{IF}\int_0^{T_\text{service}}f_\text{SM}(u)du\\
\approx\frac{1}{2}K_\text{IF,DPF}K_\text{SM,DPF}\lambda_\text{IF}\lambda_\text{SM}T_\text{service}\\
=\frac{1}{2}\lambda_\text{SM,DPF,det}\lambda_\text{IF,DPF}T_\text{service}
\tag{472.6}
$$
これは図104.2の初版PMHF式(パターン1, 2のみ)の、DPFにおけるパターン2に相当する部分と(IF⇒m, $\tau_\text{SM}$⇒$T_\text{service}$と読み替えることにより)正確に一致します。
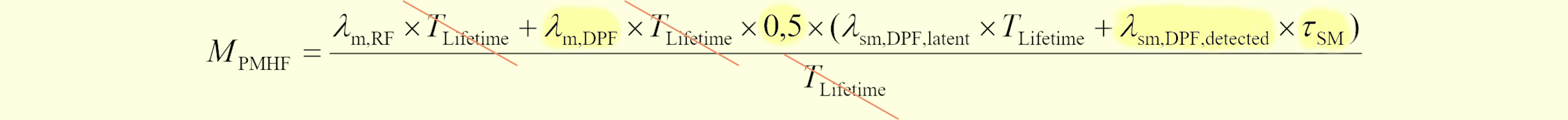 図472.2 1st edition規格第1式
図472.2 1st edition規格第1式
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。
ほぼ同様な議論ですが、記事#477に再掲します。
 前のブログ
次のブログ
前のブログ
次のブログ