前稿までの議論を踏まえ、ここからは$M_{\mathrm{PMHF}}$の計算を行います。

マルコフチェイン

図102.1にIF、SM1及び2nd SMから構成されるサブシステムの動作を表した連続時間マルコフ連鎖図(CTMC, Continuous-time Markov chains)を示します。IF、SM1のup又はdownの状態の組み合わせにより、下記の5通りの状態が存在し、その確率過程の組の遷移をマルコフ連鎖で表現します。前稿に示すように、遷移先状態確率は遷移元状態確率に微小遷移確率をかけたものを時間で積分することにより求める事ができます。以下、ステートを斜体で表します。

• IF:up, SM1:up --- OPR
• IF:down(VSG), SM1:up --- SPF
• IF:down(not VSG), SM1:up --- LAT1
• IF:up, SM1:down --- LAT2
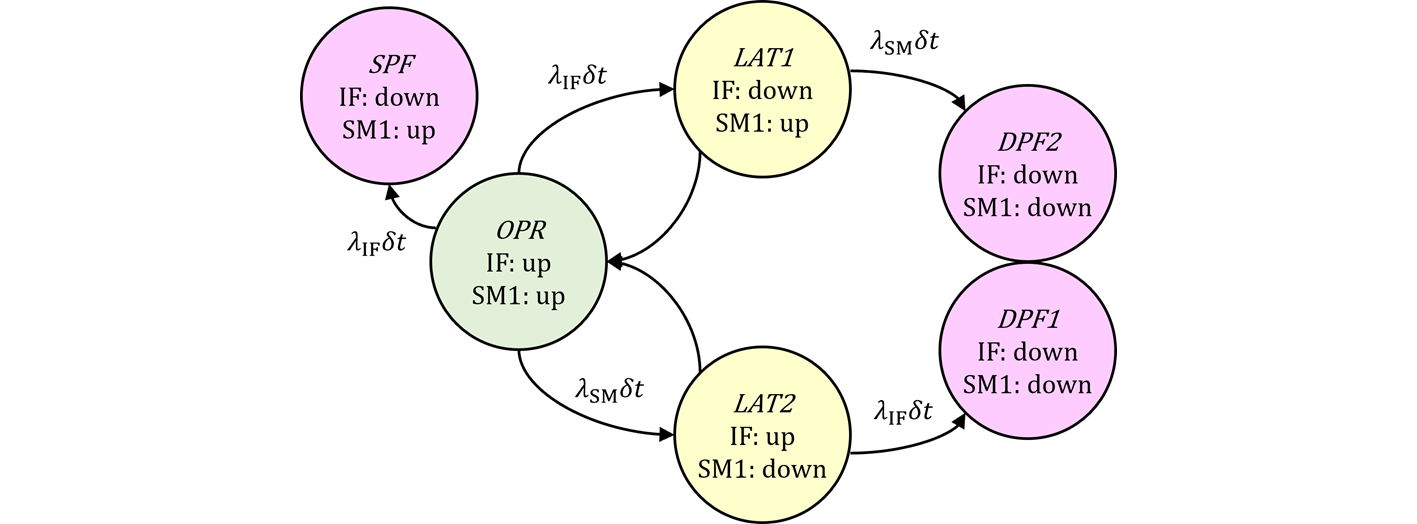
• IF:down, SM1:down --- DPF 図102.1 対象となるCTMC

リペアラビリティ(修理可能性)

一般的なサブシステムではIF、SM1共リペアラブル(修理可能)と考えます。また、検出されたフォールトは全て修理(リペア)されるという仮定を置きます。もし修理率が存在するとしても、フォールト検出率に入れてしまえば、修理率は100%として良いためです。

IF及びSM1のレイテントフォールト検出は2nd SMにより、周期$\tau$で実行されます。レイテントフォールト検出率はIF、SM1についてそれぞれ$K_\text{IF,MPF}$及び$K_\text{SM,MPF}$ですが、アンリペアラブルとする場合はレイテントフォールト検出率をゼロとすれば良いわけです。従って、リペアラブルのほうが一般的なサブシステムを表します。ISO 26262の基本思想は、定数故障率(指数分布)、周期的フォールト検出が基礎となっています。

まず、IFがアンリペアラブル、SM1がリペアラブルの場合を考えます。これをIFUモデル(IFがUnrepairable)とします。

RAMS 2020においてPMHF式の論文発表が終了したため、本記事を開示します。

前のブログ 次のブログ