|
17 |
連続時間マルコフ連鎖とPMHF式の導出 改訂版 (2) |
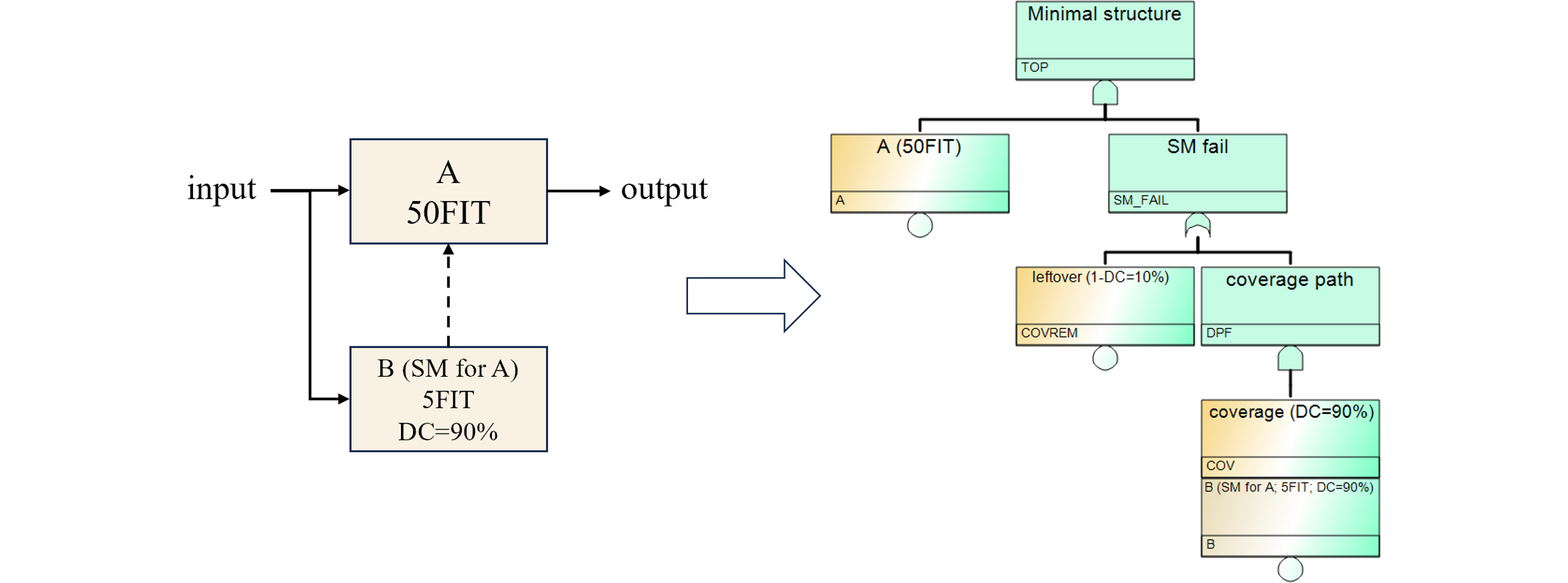
サブシステム(VSG吸収)へ持ち上げてPMHFを導出する
VSGに対応するサブシステム過程を$(\eta_t^\text{sub})_{t\ge0}$とし、
VSG集合を吸収集合$\mathcal{P}_\text{VSG}$とします。到達確率を
$$ F_\text{VSG}(t):=\Pr\{\eta_t^\text{sub}\in\mathcal P_\text{VSG}\} \tag{1058.1} $$ と定義し、区間内で微分可能なとき到達密度を $$ f_\text{VSG}(t):=\frac{d}{dt}F_\text{VSG}(t) \tag{1058.2} $$ と定義します。
非冗長系では、DPFは「SMが潜在状態のときにIF故障が起きる」ことで発生します。したがってDPFの到達密度は $$ f_\text{DPF}(t)=\lambda_\text{IF,DPF}\,Q_\text{SM}(t) \tag{1058.3} $$ と書けます。ここで $\lambda_\text{IF,DPF}=K_\text{IF,RF}\lambda_\text{IF}$ です。
DPFは「SMが潜在状態のときにIF故障が起きる」ため、DPFの到達密度は $$ f_\text{DPF}(t)=\Pr\{\text{IF up at }t\}\,\lambda_\text{IF,DPF}\,Q_\text{SM}(t) \tag{1058.3} $$ と書けます。希少事象近似の下では $\Pr\{\text{IF up at }t\}\approx 1$ なので $f_\text{DPF}(t)\approx \lambda_\text{IF,DPF}Q_\text{SM}(t)$ と簡約できます。
SPFはSM状態に依らず発生するため $$ f_\text{SPF}(t)=\lambda_\text{IF,SPF} \tag{1058.4} $$ と近似できます。ここで $\lambda_\text{IF,SPF}=(1-K_\text{IF,RF})\lambda_\text{IF}$ です。
非冗長系では $$ f_\text{VSG}(t)\approx f_\text{SPF}(t)+f_\text{DPF}(t) \tag{1058.5} $$ と置けるため $$ f_\text{VSG}(t)\approx (1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\,Q_\text{SM}(t) \tag{1058.6} $$ となります。
車両寿命を $T_\text{lifetime}$ とし、規格定義より $$ \mathrm{PMHF}:=\frac{1}{T_\text{lifetime}}PoF_\text{VSG}=\frac{1}{T_\text{lifetime}}F_\text{VSG}(T_\text{lifetime})=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_\text{VSG}(t)\,dt \tag{1058.7} $$ です。
PIR周期一定で $T_\text{lifetime}=n\tau$ とすれば $$ \int_0^{T_\text{lifetime}} Q_\text{SM}(t)\,dt=(1-K_\text{SM,DPF})\int_0^{T_\text{lifetime}}F_\text{SM}(t)\,dt+K_\text{SM,DPF}\sum_{k=0}^{n-1}\int_0^\tau F_\text{SM}(u)\,du \tag{1058.8} $$ となります。ここで(1057.6)を用いて区間分割しました。
小確率近似 $F_\text{SM}(t)\approx \lambda_\text{SM}t$ を用いれば $$ \int_0^{T_\text{lifetime}}F_\text{SM}(t)\,dt\approx \frac{\lambda_\text{SM}T_\text{lifetime}^2}{2},\quad \int_0^\tau F_\text{SM}(u)\,du\approx \frac{\lambda_\text{SM}\tau^2}{2} \tag{1058.9} $$ です。したがって $$ \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}} Q_\text{SM}(t)\,dt\approx \frac{1}{2}\lambda_\text{SM}\Bigl((1-K_\text{SM,DPF})T_\text{lifetime}+K_\text{SM,DPF}\tau\Bigr) \tag{1058.10} $$ を得ます。
(1058.6)(1058.7)(1058.10)より $$ \mathrm{PMHF}\approx (1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\Bigl((1-K_\text{SM,DPF})T_\text{lifetime}+K_\text{SM,DPF}\tau\Bigr) \tag{1058.11} $$ となります。