|
31 |
BSV(Bluespec SystemVerilog) (3) |
BSV(Bluespec SystemVerilog)によるシミュレーション
bscとは、Bluespecが最近オープンソース化したコンパイラです。詳しくは、ここを見てください。
いろいろと調整した結果、bscがインストールできました。早速、以下のようなフィボナッチモジュール(ファイル名FibOne.bsv)をコンパイルしてみます。これは、フィボナッチ数列を発生するモジュールで、前の値に次の値を加算することを繰り返すものです。
モジュールファイル:FibOne.bsv
(* synthesize *)
module mkFibOne();
// register containing the current Fibonacci value
Reg#(int) this_fib(); // interface instantiation
mkReg#(0) this_fib_inst(this_fib); // module instantiation
// register containing the next Fibonacci value
Reg#(int) next_fib();
mkReg#(1) next_fib_inst(next_fib);
rule fib; // predicate condition always true, so omitted
this_fib <= next_fib;
next_fib <= this_fib + next_fib; // note that this uses stale this_fib
$display("%0d", this_fib);
if ( this_fib > 10000 ) $finish(0) ;
endrule: fib
endmodule: mkFibOne
モジュール内にテストベンチのような\$displayや$finishの記述があるので、これだけでテストが可能です(が、モジュール設計としては良くないので、後で外します)。
BSVプログラムの説明
以下の部分は、現在の値this_fibと次の値next_fibを保持するレジスタのインスタンスです。
// register containing the current Fibonacci value
Reg#(int) this_fib(); // interface instantiation
mkReg#(0) this_fib_inst(this_fib); // module instantiation
// register containing the next Fibonacci value
Reg#(int) next_fib();
mkReg#(1) next_fib_inst(next_fib);
次のように、ruleブロックにアルゴリズム計算ルールを記述します。
this_fib <= next_fib;
next_fib <= this_fib + next_fib; // note that this uses stale this_fib
コメントにも書いているように、this_fibとnext_fibは同時に変更されるので、それぞれ、直前の値を読み込み、同時に値を更新します。
Bluesimによるシミュレーション
コンパイル及びシミュレーションモデル生成(リンク)の2段階で行います。太字が入力部分です。
$ bsc -sim FibOne.bsv
Elaborated module file created: mkFibOne.ba
$ bsc -sim -e mkFibOne -o mkFibOne.exec
Bluesim object created: mkFibOne.{h,o}
Bluesim object created: model_mkFibOne.{h,o}
Simulation shared library created: mkFibOne.exec.so
Simulation executable created: mkFibOne.exec
mkFibOne.execというbluesimの実行ファイルが生成されたので起動します。
$ ./mkFibOne.exec
0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
10946
Verlogの生成
次に、確認のためにverilogシミュレーションを実行します。まずbscにより、モジュールを合成可能なVerilogコードにコンパイルします。
$ bsc -verilog FibOne.bsv
Verilog file created: mkFibOne.v
生成されたファイル名はモジュール名+".v"(mkFibOne.v)となります。
モジュールファイル:mkFibOne.v
//
// Generated by Bluespec Compiler (build 38534dc)
//
// On Mon Mar 23 06:33:47 JST 2020
//
//
// Ports:
// Name I/O size props
// CLK I 1 clock
// RST_N I 1 reset
//
// No combinational paths from inputs to outputs
//
//
`ifdef BSV_ASSIGNMENT_DELAY
`else
`define BSV_ASSIGNMENT_DELAY
`endif
`ifdef BSV_POSITIVE_RESET
`define BSV_RESET_VALUE 1'b1
`define BSV_RESET_EDGE posedge
`else
`define BSV_RESET_VALUE 1'b0
`define BSV_RESET_EDGE negedge
`endif
module mkFibOne(CLK,
RST_N);
input CLK;
input RST_N;
// register next_fib_inst
reg [31 : 0] next_fib_inst;
wire [31 : 0] next_fib_inst$D_IN;
wire next_fib_inst$EN;
// register this_fib_inst
reg [31 : 0] this_fib_inst;
wire [31 : 0] this_fib_inst$D_IN;
wire this_fib_inst$EN;
// register next_fib_inst
assign next_fib_inst$D_IN = this_fib_inst + next_fib_inst ;
assign next_fib_inst$EN = 1'd1 ;
// register this_fib_inst
assign this_fib_inst$D_IN = next_fib_inst ;
assign this_fib_inst$EN = 1'd1 ;
// handling of inlined registers
always@(posedge CLK)
begin
if (RST_N == `BSV_RESET_VALUE)
begin
next_fib_inst <= `BSV_ASSIGNMENT_DELAY 32'd1;
this_fib_inst <= `BSV_ASSIGNMENT_DELAY 32'd0;
end
else
begin
if (next_fib_inst$EN)
next_fib_inst <= `BSV_ASSIGNMENT_DELAY next_fib_inst$D_IN;
if (this_fib_inst$EN)
this_fib_inst <= `BSV_ASSIGNMENT_DELAY this_fib_inst$D_IN;
end
end
// synopsys translate_off
`ifdef BSV_NO_INITIAL_BLOCKS
`else // not BSV_NO_INITIAL_BLOCKS
initial
begin
next_fib_inst = 32'hAAAAAAAA;
this_fib_inst = 32'hAAAAAAAA;
end
`endif // BSV_NO_INITIAL_BLOCKS
// synopsys translate_on
// handling of system tasks
// synopsys translate_off
always@(negedge CLK)
begin
#0;
if (RST_N != `BSV_RESET_VALUE) $display("%0d", $signed(this_fib_inst));
if (RST_N != `BSV_RESET_VALUE)
if ((this_fib_inst ^ 32'h80000000) > 32'h80002710) $finish(32'd0);
end
// synopsys translate_on
endmodule // mkFibOne
テストベンチの作成
bluesimは暗黙のクロックやリセットが動作するため、テストベンチ無しでもシミュレーションが実行できました。一方verilogではそのような機能は無いので以下のようなテストベンチ(ファイル名tbmkFibOne.v)を用意します。
テストベンチ中の/AUTO〇〇/という記述は、emacsのverilog modeによるインスタンスやポートの自動生成の機能です。C-c C-aにより、面倒なポートリストやインスタンス部分が自動生成できます。テストベンチでは、モジュールへの入力用に/AUTOREGINPUT/と、モジュールからの出力用に/AUTOWIRE/を指定しておきます。
テストベンチファイル:tbmkFibOne.v
`timescale 1ns/1ps
module tb_mkFibOne;
/*AUTOREGINPUT*/
// Beginning of automatic reg inputs (for undeclared instantiated-module inputs)
reg CLK; // To mkFibOne of mkFibOne.v
reg RST_N; // To mkFibOne of mkFibOne.v
// End of automatics
/*AUTOWIRE*/
mkFibOne mkFibOne (/*AUTOINST*/
// Inputs
.CLK (CLK),
.RST_N (RST_N));
initial begin
RST_N = 1'b0;
#30;
RST_N = 1'b1;
end
initial begin
CLK = 1'b0;
forever begin
#5;
CLK = ~CLK;
end
end
initial begin
$dumpfile("tbmkFibOne.vcd");
$dumpvars(0,mkFibOne);
end
endmodule
Verilogシミュレーションの実行
iverilogにより実行ファイルmkFibOne.exevを生成し、シミュレーションを実行すると、同じ結果となりました。
$ iverilog tbmkFibOne.v mkFibOne.v -o mkFibOne.exev
$ ./mkFibOne.exev
VCD info: dumpfile tbmkFibOne.vcd opened for output.
0
1
1
2
3
5
8
13
21
34
55
89
144
233
377
610
987
1597
2584
4181
6765
10946
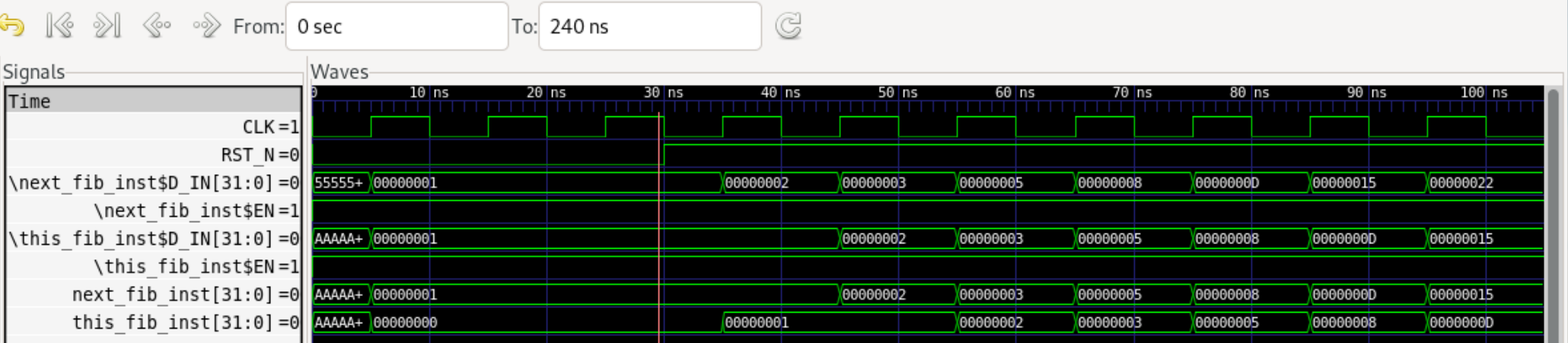
波形ビュワーであるgtkwaveを起動します。verilogシミュレーションで生成したVCDファイルを指定します。
$ gtkwave -f tbmkFibOne.vcd
GTKWave Analyzer v3.3.111 (w)1999-2020 BSI
[0] start time.
[520000] end time.
verilogシミュレーションの波形をgtkwaveで表示します。