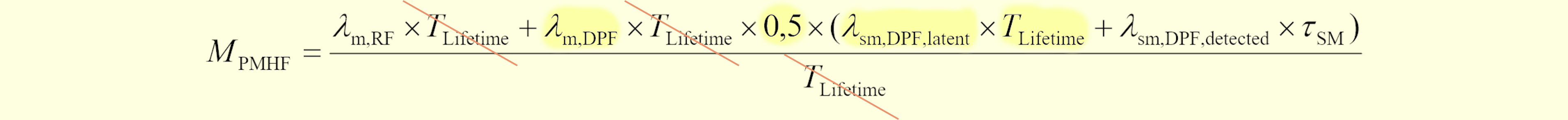パターン1

規格解説書によるPMHF式の導出手法と、弊社による導出手法を比較します。簡単化のため(及びパターン2は解説書は積分範囲に誤りがあるため)、パターン1どうしを比較しそれぞれ規格解説書=com、弊社=fsmとします。

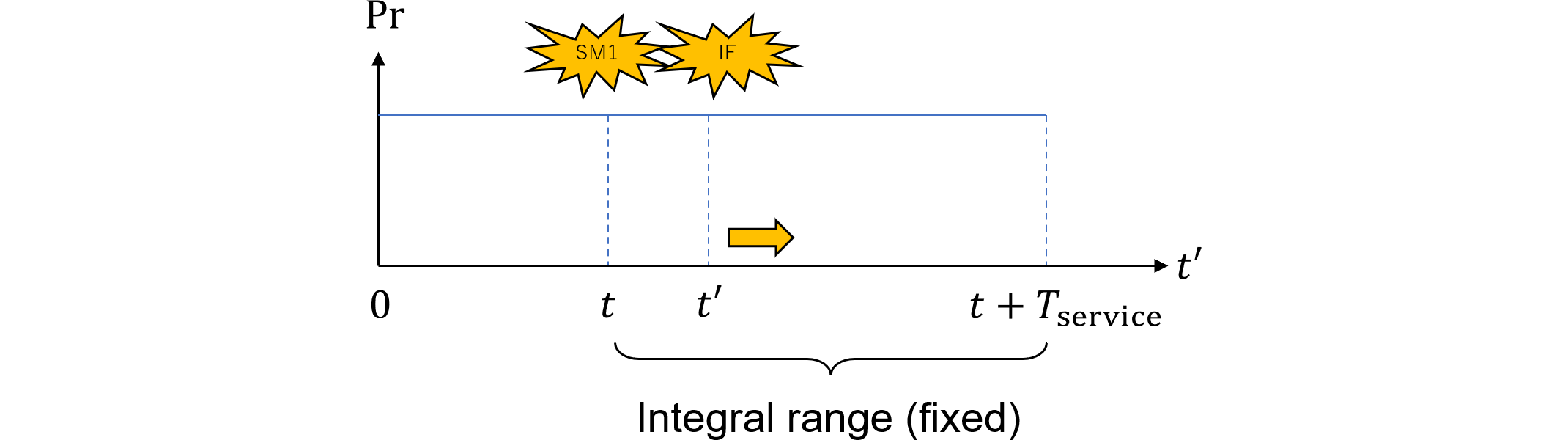
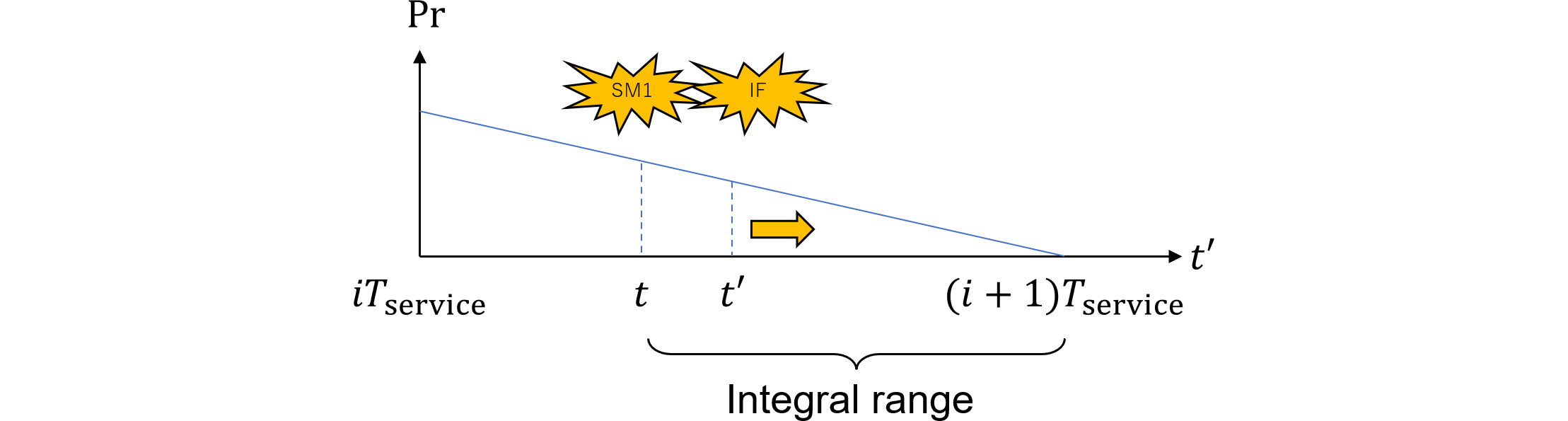
まず、規格解説書パターン1(476.6)は、 $$ \require{color} \definecolor{yellow}{rgb}{1.0,1.0,0.8} \definecolor{lime}{rgb}{0.8,1.0,0.9} \definecolor{water}{rgb}{0.8,0.9,1.0} \definecolor{pink}{rgb}{1.0,0.8,1.0} \definecolor{red}{rgb}{1.0,0.8,0.8} \definecolor{orange}{rgb}{1.0,0.9,0.8} M_\text{PMHF,com,P1}=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{SM1 down in }[t, t+\delta t)\cap\text{SM1 up at }t\\ \cap\colorbox{pink}{$\text{SM1 undetected}$}\}\cdot\colorbox{lime}{$\Pr\{\text{IF up at }t \cap\text{IF fails in }[t, T_\text{lifetime})$}\\ \cap\colorbox{water}{$\text{IF prevented}$}\} \tag{478.1} $$

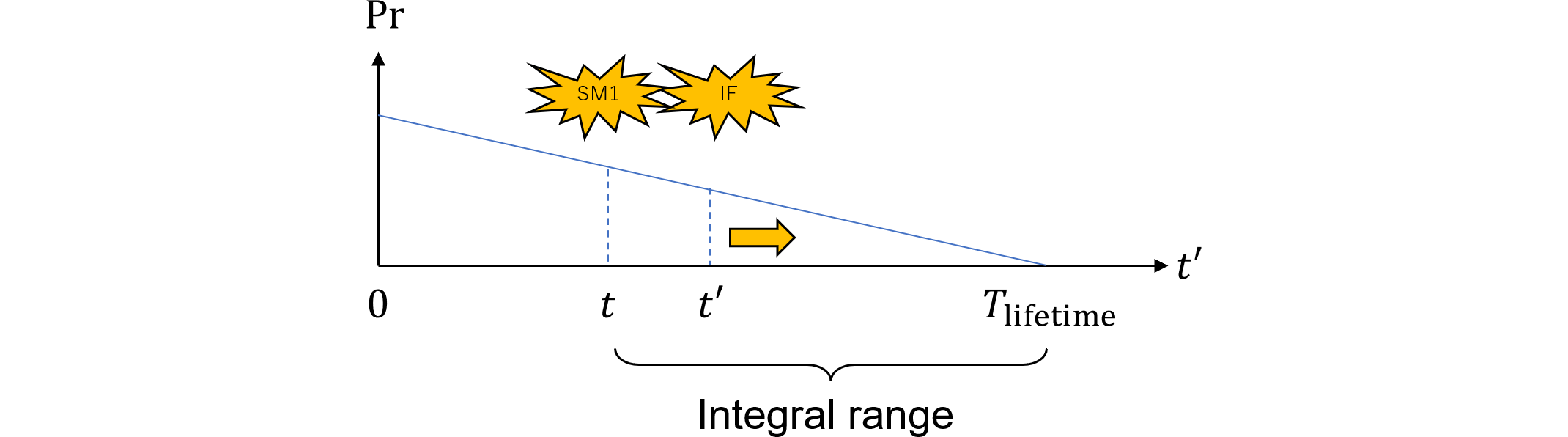
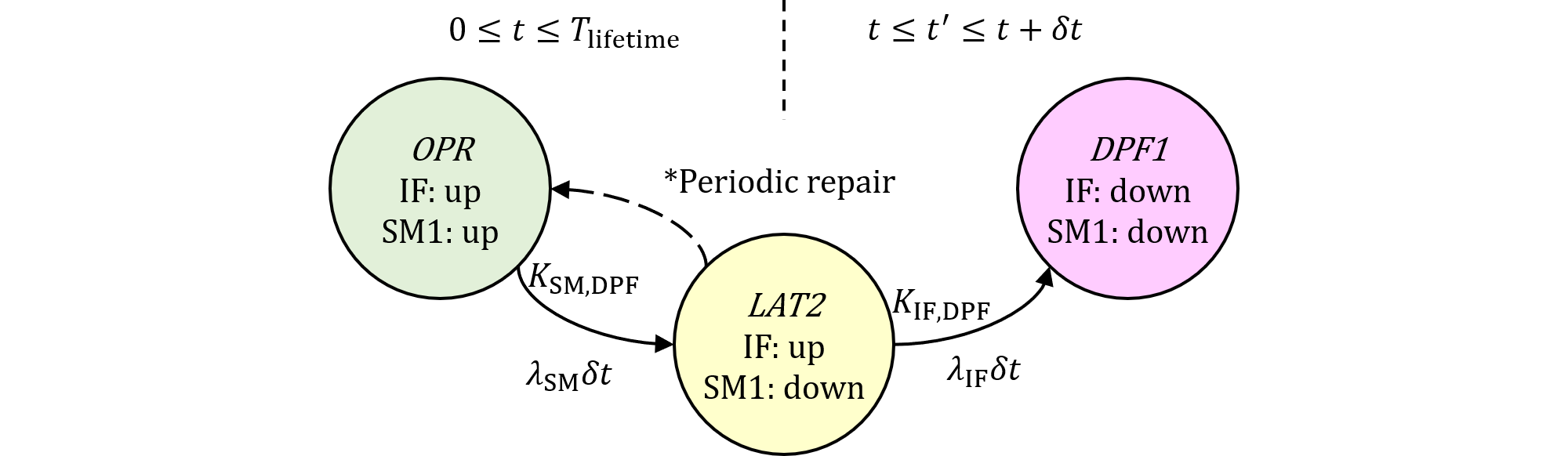
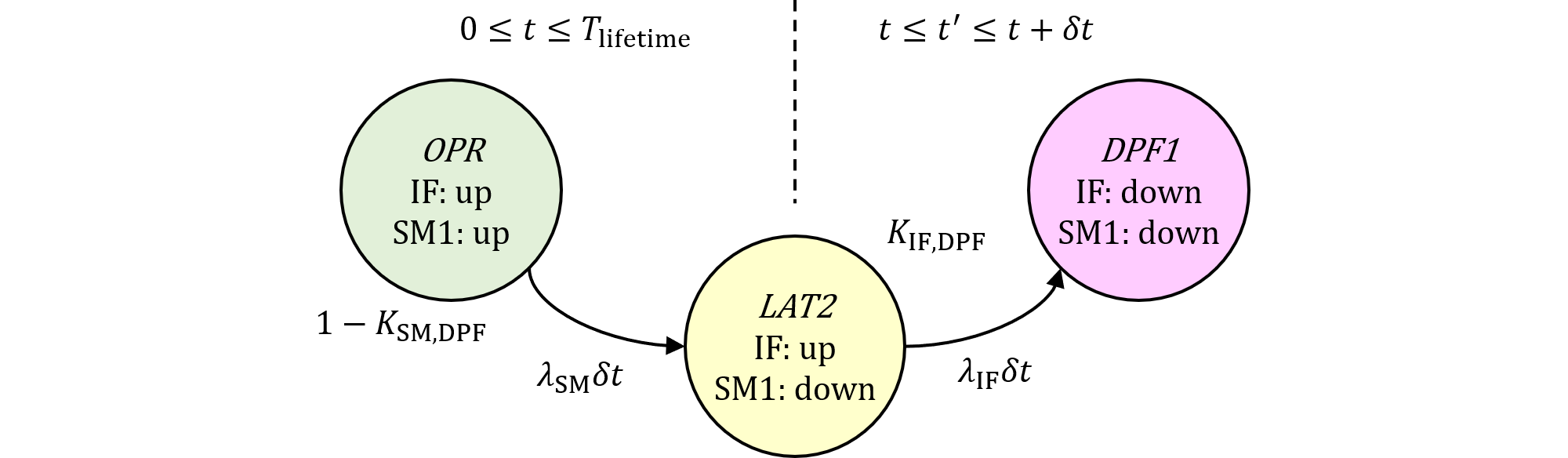
一方、弊社パターン1(474.5)は、 $$ M_\text{PMHF,fsm,P1}=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\colorbox{orange}{$\text{LAT2 at }t$}\cap\colorbox{water}{$\text{IF prevented}$}\\ \cap\text{IF down in }(t', t'+\delta t']\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{IF up at }t'\cap\colorbox{orange}{$\text{SM1 down at }t$}\cap\colorbox{pink}{$\text{SM1 not detected}$}\\ \cap\colorbox{water}{$\text{IF prevented}$}\cap\text{IF down in }(t', t'+\delta t']\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\colorbox{orange}{$\Pr\{\text{SM1 fails in }[0, t)$}\cap\colorbox{pink}{$\text{SM1 not detected}$}\}\\ \cdot d\!\Pr\{\text{IF down in }[t', t'+\delta t')\cap\text{IF up at }t'\cap\colorbox{water}{$\text{IF prevented}$}\} \tag{478.2} $$ でした。

ここで、以下(478.3)の2つの確率 $$ \begin{eqnarray}\begin{cases} \Pr\{\colorbox{pink}{$\text{SM1 undetected}$}\}=\colorbox{pink}{$1-K_\text{SM1,DPF}$}\\ \Pr\{\colorbox{water}{$\text{IF prevented}$}\}=\colorbox{water}{$K_\text{IF,DPF}$} \end{cases}\end{eqnarray}\tag{478.3} $$ は定数であることから、この(478.3)を代入すれば、(478.1)は、 $$ (478.1)=M_\text{PMHF,com,P1}=\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$}\\ \cdot\int_0^{T_\text{lifetime}}d\!\Pr\{\text{SM1 down in }[t, t+\delta t)\cap\text{SM1 up at }t\}\\ \cdot\colorbox{lime}{$\Pr\{\text{IF up at }t'\cap\text{IF fails in }[t, T_\text{lifetime})\}$} \tag{478.4} $$ となり、(478.2)は、 $$ (478.2)=M_\text{PMHF,fsm,P1}=\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$}\\ \cdot\int_0^{T_\text{lifetime}}\colorbox{orange}{$\Pr\{\text{SM1 fails in }[0, t')\}$}\cdot d\!\Pr\{\text{IF down in }[t', t'+\delta t')\cap\text{IF up at }t'\} \tag{478.5} $$ となります。それぞれに(66.4)を適用すれば、(478.4)は、 $$ (478.4)=M_\text{PMHF,com,P1}=\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$}\\ \cdot\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\colorbox{lime}{$\Pr\{\text{IF up at }t\cap\text{IF fails in }[t, T_\text{lifetime})\}$}dt\\ =\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$}\\ \cdot\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\colorbox{lime}{$\left[\Pr\{\text{IF fails in }[0, T_\text{lifetime})\}-\Pr\{\text{IF fails in }[0, t)\}\right]$}dt\\ =\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$} \int_0^{T_\text{lifetime}}f_\text{SM1}(t)\colorbox{lime}{$\left[F_\text{IF}(T_\text{lifetime})-F_\text{IF}(t)\right]$}dt\\ \tag{478.6} $$ となり、(478.5)は、 $$ (478.5)=M_\text{PMHF,fsm,P1}\\ =\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1-K_\text{SM1,DPF})$}\int_0^{T_\text{lifetime}}\Pr\{\colorbox{orange}{$\text{SM1 fails in }[0, t')$}\}f_\text{IF}(t')dt'\\ =\frac{1}{T_\text{lifetime}}\colorbox{water}{$K_\text{IF,DPF}$}\colorbox{pink}{$(1- K_\text{SM1,DPF})$}\int_0^{T_\text{lifetime}}\colorbox{orange}{$F_\text{SM1}(t)$}f_\text{IF}(t)dt \tag{478.7} $$ となります。$t'$を$t$に置き換えても値は変わりません。(478.6)も(478.7)も結果式は同一であり、 $$ (478.6)=(478.7)=\frac{1}{2}K_\text{IF,DPF}K_\text{SM,DPF}\lambda_\text{IF}\lambda_\text{SM1}T_\text{service} \tag{478.8} $$ と、このように一致します。従って元の(478.1)と(478.2)は同値であるはずです。

ここで(478.6)、(478.7)のそれぞれの意味を解析してみます。(478.6)の解説書の方法は、

SM1のフォールトの確率密度を、$t$をSM1のフォールト時刻として0から車両寿命まで積分するにあたり、

1. 0から$t$まではIFが先にフォールトしている場合のIFの先フォールトの確率(=確率密度の積分)
2. $t$から車両寿命まではSM1が先にフォールトしている場合のIFの後フォールトの確率(=確率密度の積分)

の合計$\colorbox{lime}{$F_\text{IF}(T_\text{lifetime})$}$を求めます。これから1.$\colorbox{lime}{$F_\text{IF}(t)$}$を引けば、結果としてSM1⇒IFの順のDPF確率が求まります。

このようなことをせずにCTMCを用いて(478.7)のとおり、

IFのフォールトの確率密度を、$t'$をIFのフォールト時刻として0から車両寿命まで積分するにあたり、

1. 0から$t'$まではSM1が先にフォールトしている場合のSM1の先フォールトの確率(=確率密度の積分)

である$\colorbox{orange}{$F_\text{SM1}(t')$}$を先に求めれば、結果としてDPFを単純に求めることができます。時系列的にもSM1⇒IFの順のフォールトなので、最初にSM1のフォールト確率積分をするほうが自然です。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ

パターン2

次にパターン2です。図477.1にISO 26262第2版解説書のパターン2の導出過程を引用します。

解説書で示される導出過程の誤り原因は3つあり、前稿(476.3)で指摘した(マイナーな)2つの他、重大な誤りなのがIFのフォールトの積分範囲です。

図477.1によれば、時刻$t$がSM1のフォールト発生時刻、時刻$t'$が引き続くIFのフォールト発生時刻であり、(477.1)に$t$と$t'$の制約を示します。 $$ \begin{eqnarray} \begin{cases} t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime} \\ t': \text{Time of fault of IF}, t\le t'\le \color{red}{t+T_\text{service}}\quad\quad\color{red}{(誤りであるため注意)} \end{cases} \end{eqnarray}\tag{477.1} $$

IFのフォールトの積分範囲、つまり$t'$の範囲は$t$から$t+T_\text{service}$となっていますが、図477.2のように、$t$が大となっても積分範囲は常に一定値$T_\text{service}$となることが問題です。

なぜなら、SM2によるSM1の検査・修理は、SM1のフォールト時点$t$によらず一定周期$T_\text{service}$で実施されるため、図477.2の方法では$t$に依存して暴露終了時刻がズレていきます。暴露終了時刻が$t$に依存しなければ、本来$t'$が$t$から離れるほど、IFのフォールト発生確率は小さくなるはずです。

区間$(0, T_\text{lifetime}]$中に検査周期である$T_\text{service}$は$n\equiv\frac{T_\text{lifetime}}{T_\text{service}}$個あります。$i$番目の周期は図477.3のように区間$(iT_\text{service},(i+1)T_\text{service}]$で表され、$t'$はその中でのみ積分されます。従って積分範囲は図477.3のようになるべきです。

従って、$t$と$t'$の制約は(477.2)となります。 $$ \begin{eqnarray} \begin{cases} t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime},\ \ s.t.\ \ iT_\text{service}\le t\ \lt(i+1)T_\text{service}\\ t': \text{Time of fault of IF}, t\le t'\le \color{green}{(i+1)T_\text{service}} \end{cases} \end{eqnarray}\tag{477.2} $$

パターン2は、SM2によりSM1のフォールトが検出可能な部分であるため、SM1のフォールトは起きたとしても検査・修理周期内でしかレイテントとなりえません。図477.3のように、$i$番目の検査周期でフォールトが起きたとすれば、$i+1$番目の周期までに修理されることになります。積分範囲はたかだか$T_\text{service}$であり、解説書のように$T_\text{service}$一定値ではありません。

準備ができたので、基本的には規格の流儀で計算しますが、先に誤りを修正します。IFに関する修正点は前稿と同様で、以下の2点です。 $$ \begin{eqnarray} \begin{cases} R_\text{IF}(t)&\Rightarrow&R_\text{IF}(t')\quad\quad\text{(up条件)}\\ f_\text{IF,DPF}(t')&\Rightarrow&\lambda_\text{IF,DPF}\quad\quad\text{(down条件)} \end{cases} \end{eqnarray}\tag{476.3} $$

(476.3)及び上記積分範囲の修正を適用し、前稿と同様に(476.4)に対応する式を示せば、 $$ \begin{eqnarray} &&\Pr\{\text{IF is in }LAT2S\cap\text{IF fails in }[t, (i+1)T_\text{service})\}\\ &=&\Pr\{\text{IF up at }t\cap\text{IF prevented}\cap\text{IF fails in }[t, (i+1)T_\text{lifetime})\}\\ &=&\Pr\{\text{IF prevented}\}\int_t^{(i+1)T_\text{lifetime}}d\!\Pr\{\text{IF down in }[t', t'+dt')\cap\text{IF up at }t'\}\\ &=&K_\text{IF, DPF}\int_t^{(i+1)T_\text{service}}d\!\Pr\{\text{IF down in }[t', t'+dt')\ |\ \text{IF up at }t'\}\cdot\Pr\{\text{IF up at }t'\}\\ &=&K_\text{IF,DPF}\int_t^{(i+1)T_\text{service}}\lambda_\text{IF}R_\text{IF}(t')dt' =K_\text{IF,DPF}\int_t^{(i+1)T_\text{service}}f_\text{IF}(t')dt'\\ &=&K_\text{IF,DPF}\left\lbrack F_\text{IF}(t')\right\rbrack_t^{(i+1)T_\text{service}} =K_\text{IF,DPF}\left[F_{\text{IF}}((i+1)T_\text{service})-F_\text{IF}(t)\right]\\ &\approx&K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right) \end{eqnarray}\tag{477.3} $$ と表せます。前稿で述べたように解説書の2か所の誤りが確認できます。

(477.3)により$t$におけるIFの車両寿命までのフォールト確率を表せました。$t\le t'$の条件下ではSM1とIFのフォールトの生起確率は独立として掛け合わせることができます。従って$t$を周期的な変数$u\equiv t \bmod T_\text{service}$とその逆の関係である$t=iT_\text{service}+u, i=0, 1, 2, ..., n-1$で表せば、パターン2のPMHFは、 $$ \begin{eqnarray}\require{cancel} M_\text{PMHF,P2}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{SM1 down in }[t, t+dt)\cap\text{SM1 detected}\\ &&\cap\ \text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}\Pr\{\text{SM1 detected}\}\sum_{i=0}^{n-1}\int_{iT_\text{service}}^{(i+1)T_\text{service}}d\!\Pr\{\text{SM1 down in }[t, t+dt)\ |\ \\ &&\text{SM1 up at }t\}\Pr\{\text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}K_\text{SM1,DPF}\sum_{i=0}^{n-1}\int_{iT_\text{service}}^{(i+1)T_\text{service}}\lambda_\text{SM1}R_\text{SM1}(t)\\ &&\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left((i+1)T_\text{service}-t\right)\right\}dt \end{eqnarray}\tag{477.4} $$ ここで、等比級数の公式と、$x\ll1$の際のマクローリン近似$e^{-x}\approx1-x$を用いて、 $$ \begin{eqnarray}\require{cancel} &=&\frac{1}{T_\text{lifetime}}n K_\text{SM1,DPF}K_\text{IF,DPF}\int_0^{T_\text{service}}\lambda_\text{SM1}R_\text{SM1}(u)\lambda_\text{IF}\left(T_\text{service}-u\right)du\\ &=&\frac{1}{\bcancel{T_\text{lifetime}}}\frac{\bcancel{T_\text{lifetime}}}{T_\text{service}}K_\text{SM1,DPF}K_\text{IF,DPF}\int_0^{T_\text{service}}f_\text{SM1}(u)\lambda_\text{IF}\left(T_\text{service}-u\right)du\\ &\approx&\frac{1}{\bcancel{T_\text{service}}}K_\text{SM1,DPF}K_\text{IF,DPF}\lambda_\text{IF}\lambda_\text{SM1}\left\lbrack T_\text{service}\bcancel{u}-\frac{1}{2}u^\bcancel{2}\right\rbrack_0^{T_\text{service}}\\ &=&\frac{1}{2}K_\text{IF,DPF}K_\text{SM1,DPF}\lambda_\text{IF}\lambda_\text{SM1}T_\text{service}\\ &=&\frac{1}{2}\lambda_\text{SM1,DPF,det}\lambda_\text{IF,DPF}T_\text{service} \end{eqnarray}\tag{477.5} $$ となります。なお、式変形中に弊社積分公式(471.3)を使用しています。

結果の(477.5)と、次の図477.4に引用する規格第2版式のパターン2を比較すると、規格式の値は2倍大きく、これは前述のとおりIFのフォールトに関する積分範囲が過剰なことに因るものです。

一方、(477.5)は次の図477.5に引用する規格初版式のパターン2に相当する部分(黄色部分)と(IF⇒m, $T_\text{service}$⇒$\tau_\text{SM}$と読み替えることにより)正確に一致します。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ

パターン1

再度、ISO 26262第2版解説書に示された導出過程に沿ってPMHF式を導出します。この導出過程によればパターン2に重大な誤りがあります。その原因はIFのフォールトの積分範囲なのですが、次稿で説明します。

図309.1の再掲になりますが図476.1に解説書のパターン1の導出過程を引用します。

時刻$t$がSM1のフォールト発生時刻、時刻$t'$が引き続くIFのフォールト発生時刻です。$t$と$t'$の制約を示します。 $$ \begin{eqnarray} \begin{cases} t: \text{Time of fault of SM1}, 0\le t\le T_\text{lifetime} \\ t': \text{Time of fault of IF}, t\le t'\le T_\text{lifetime} \end{cases} \end{eqnarray}\tag{476.1} $$

図476.1ではパターン1のIFのフォールトの積分範囲、つまり$t'$の範囲は$t\le t'\le T_\text{lifetime}$となっています。従って、$t$が大となるに従って$t'$の範囲が狭くなり、IFのフォールト発生確率も小さくなります。つまり、$t$と$\Pr\{\text{IF fails at }t'\}$は逆相関の関係があります。

基本的には解説書に従った導出過程で計算しますが、誤りを修正します。まずIFのフォールトに関する積分である、「時刻$t$までup、かつ、$t'$でフォールトする確率」という以下の式(476.2)(図476.1から抜粋引用)は $$ \int_t^{T_\text{lifetime}}f_\text{IF,DPF}(t')dt'\cdot R_\text{IF}(t)\quad\quad\color{red}{(誤りであるため注意)} \tag{476.2} $$ (476.3)に示す2か所が誤りとその修正です。ただしこの誤りはたまたま結果に影響しません。 $$ \begin{eqnarray} \begin{cases} R_\text{IF}(t)&\Rightarrow&R_\text{IF}(t')\quad\quad\text{(up条件)}\\ f_\text{IF,DPF}(t')&\Rightarrow&\lambda_\text{IF,DPF}\quad\quad\text{(down条件)} \end{cases} \end{eqnarray}\tag{476.3} $$

(476.3)はIFに関するup条件及びdown条件ですが、この両者は同じIFに関する事象であるため独立ではありません。down条件に関しては(66.8)で示す条件付き確率を用いる必要があります。従って(476.2)を(476.4)のように、「時刻$t'$までup、かつ、$t'$でフォールトする条件付き確率」と修正します。するとIFのフォールトに関する確率(476.2)は、 $$ \begin{eqnarray} &&\Pr\{\text{IF is in }LAT2S\cap\text{IF fails in }[t, T_\text{lifetime})\}\\ &=&\Pr\{\text{IF up at }t\cap\text{IF prevented}\cap\text{IF fails in }[t, T_\text{lifetime})\}\\ &=&\Pr\{\text{IF prevented}\}\int_t^{T_\text{lifetime}}\Pr\{\text{IF down in }[t', t'+dt')\cap\text{IF up at }t'\}\\ &=&K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\Pr\{\text{IF down in }[t', t'+dt')\ |\ \text{IF up at }t'\}\cdot\Pr\{\text{IF up at }t'\}\\ &=&K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\lambda_\text{IF}R_\text{IF}(t')dt'=K_\text{IF, DPF}\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\\ &=&K_\text{IF, DPF}\left\lbrack F_\text{IF}(t')\right\rbrack_t^{T_\text{lifetime}}=K_\text{IF, DPF}\left[F_{\text{IF}}(T_\text{lifetime})-F_\text{IF}(t)\right]\\ &\approx&K_\text{IF, DPF}\lambda_\text{IF}\left(T_\text{lifetime}-t\right) \end{eqnarray} \tag{476.4} $$ と表せます。ここで途中の式

$$ K_\text{IF, DPF}\int_t^{T_\text{lifetime}}\lambda_\text{IF}R_\text{IF}(t')dt'=\int_t^{T_\text{lifetime}}\lambda_\text{IF,DPF}R_\text{IF}(t')dt' \tag{476.5} $$ と(476.2)を比較すると、(476.3)で示した解説書の2点の誤りが確認できます。

(476.4)により$t$におけるIFの車両寿命までのフォールト確率を表せました。$t\le t'$の条件下ではSMとIFのフォールトの確率は独立として掛け合わせることができるので、パターン1のPMHFは、 $$ \require{cancel} \begin{eqnarray} M_\text{PMHF,P1}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\text{SM1 down in }[t, t+dt)\cap\text{SM1 undetected}\\ & &\cap\ \text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}\Pr\{\text{SM1 undetected}\}\int_0^{T_\text{service}}\Pr\{\text{SM1 down in }[t, t+dt)\ |\ \text{SM1 up at }t\}\\ & &\cdot\Pr\{\text{SM1 up at }t\}\cdot\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{service}-t\right)\right\}\\ &=&\frac{1}{T_\text{lifetime}}(1-K_\text{SM1,DPF})\int_0^{T_\text{lifetime}}\lambda_\text{SM1}R_\text{SM1}(t)\left\{K_\text{IF,DPF}\lambda_\text{IF}\left(T_\text{lifetime}-t\right)\right\}dt\\ &=&\frac{1}{T_\text{lifetime}}(1-K_\text{SM1,DPF})K_\text{IF,DPF}\int_0^{T_\text{lifetime}}f_\text{SM1}(t)\lambda_\text{IF}\left(T_\text{lifetime}-t\right)dt\\ &\approx&\frac{1}{\bcancel{T_\text{lifetime}}}(1-K_\text{SM1,DPF})K_\text{IF,DPF}\lambda_\text{IF}\lambda_\text{SM1}\left\lbrack T_\text{lifetime}\bcancel{t}-\frac{1}{2}t^\bcancel{2}\right\rbrack_0^{T_\text{lifetime}}\\ &=&\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM1,DPF})\lambda_\text{IF}\lambda_\text{SM1}T_\text{lifetime}\\ &=&\frac{1}{2}\lambda_\text{SM1,DPF,lat}\lambda_\text{IF,DPF}T_\text{lifetime} \end{eqnarray} \tag{476.6} $$ となります。なお、式変形中に弊社積分公式(471.3)を使用しています。

結果の(476.6)は次の図476.3に引用する規格第2版式のパターン1と正確に一致します。導出のベースがIFUモデルとなっているのが理由です。

さらに(476.6)は、次の図476.4に引用する規格初版第1式のパターン1に相当する部分(黄色部分)とも(IF⇒mと読み替えることにより)正確に一致します。導出のベースがIFUモデルとなっているのが理由です。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ

パターン2

続いてパターン2です。弊社のやり方はCTMCの原理を用い、時刻$t$におけるDPF確率密度を求め、$0$から$T_\text{lifetime}$まで積分するというものです。

• Pattern 2: SM1⇒IFの順にフォールトが発生し、SM1のフォールトは、SM2によって緩和され通知される。フォールトの暴露時間は、運転手が修理のために車両を持ち込むのに必要な予想される時間。

これはSM1のフォールトが2nd SMの定期周期$T_\text{service}$により検査され、検出割合は$K_\text{SM,DPF}$でありその全量が修理されるパターンです。時刻$t$までに最初のSM1のフォールトが起き、それ以降$t'(>=t)$がVSGとなる2つ目のIFのフォールトが起きた時刻とします。

同様に、IFのフォールトに関する$t$から$t+\delta t$までのDPF確率密度を求めます。次にサブシステムについて、DPF VSGとなる確率密度を0から$T_\text{lifetime}$まで積分します。

まず、検出される部分のSM1は周期的に修理されるため、SM1の$LAT2$での状態確率は、$u\equiv t\bmod T_\text{service}$とすれば、 $$ \begin{eqnarray} \Pr\{\text{SM1(det) in }LAT2\}&=&\Pr\{\text{SM1 down at }u\cap\text{SM1 fault detected}\}\\ &=&K_\text{SM,DPF}F_\text{SM}(u) \end{eqnarray}\tag{475.1} $$

次にIFの$LAT2$での状態確率は、 $$ \begin{eqnarray} \Pr\{\text{IF in }LAT2\}&=&\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\} =K_\text{IF,DPF}R_\text{IF}(t) \end{eqnarray}\tag{475.2} $$

$LAT2$から$DPF1$への微小時間間隔$\delta t$での遷移確率は、IFがフォールトによりDPFとなる場合であり、 $$ \Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}=\lambda_\text{IF}\delta t \tag{475.3} $$ 従って、状態確率(475.2)と遷移確率(475.3)の積をとりIFの$(t,t+\delta t]$における確率密度を求めれば、 $$ \begin{eqnarray} \Pr\{\text{IF in }LAT2&\text{ at }&t\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\}\\ &&\cdot\Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}\\ &=&K_\text{IF,DPF}R_\text{IF}(t)\lambda_\text{IF}\delta t=K_\text{IF,DPF}f_\text{IF}(t)\delta t \end{eqnarray}\tag{475.4} $$

IFとSM1にはフォールトの生起について独立であるため、各々の確率はかけることができます。よって、 IFの項(475.4)とSM1の項(475.1)の積をとり、$0$から$T_\text{lifetime}$まで積分して時間平均をとると、 $$ \begin{eqnarray} M_\text{PMHF,P2}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{LAT2 at }t\cap\text{IF fault prevented}\\ &&\cap\ \text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{IF up at }t\cap\text{SM1 down at }u\cap\text{SM1 fault detected}\\ &&\cap\ \text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\text{SM1 down at }u\cap\text{SM1 fault detected}\}\\ &&\cdot d\!\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}K_\text{SM,DPF}F_\text{SM}(u)K_\text{IF,DPF}f_\text{IF}(t)dt\\ &\approx&\frac{1}{2}K_\text{IF,DPF}K_\text{SM,DPF}\lambda_\text{IF}\lambda_\text{SM}T_\text{service}\\ &=&\frac{1}{2}\lambda_\text{SM,DPF,det}\lambda_\text{IF,DPF}T_\text{service} \end{eqnarray}\tag{475.5} $$ なお、式変形中に弊社積分公式を使用しています。

(475.5)と、図475.2に引用する規格第2版式のPattern 2を比較すると、規格式の値は不一致となります。

また、(475.5)は図475.3に引用する規格初版式のパターン2に相当する部分と(IF⇒m, $T_\text{service}$⇒$\tau_\text{SM}$と読み替えることにより)正確に一致します。

規格第2版の式はパターン2がおかしく、SM1の周期的修理性を考慮に入れていません。さらにIFのフォールトの露出時間が$t$から$t+T_\text{service}$となっているため、結果式図475.2は誤っています。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ

「ISO 26262第2版解説書」(日本規格協会)のPMHF式と別の方法ですが、弊社の方法で計算し直します。弊社のやり方はCTMCの原理を用い、時刻$t$におけるDPF確率密度を求め、$0$から$T_\text{lifetime}$まで積分するというものです。

パターン1

• Pattern 1: SM1⇒IFの順にフォールトが発生し、SM1のフォールトはSM2によって緩和されるが通知されない、または緩和されない。フォールトの暴露時間は、最悪の場合の暴露時間である車両寿命となる。

パターン1は、SM1のフォールトが2nd SM(SM2)で検出されないため、SM1のフォールト全体に対するパターン1の割合は$1-K_\text{SM,DPF}$となり、マルコフ図は以下のようになります。時刻パラメータ$t$までに最初のSMのフォールトが起き、$t'(\approx t)$がVSGとなる2つ目のIFのフォールトが起きた時刻とします。

PMHFの求め方は、IFのフォールトに関する$t$から$t+\delta t$までのDPF確率密度を求めます。次にサブシステムについて、DPF VSGとなる確率密度を0から$T_\text{lifetime}$まで積分します。

まず、検出されない部分のSM1の$LAT2$での状態確率は、 $$ \begin{eqnarray} \Pr\{\text{SM1(undet) in }LAT2\}&=&\Pr\{\text{SM1 down at }t\cap\text{SM1 fault not detected}\}\\ &=&(1-K_\text{SM,DPF})F_\text{SM}(t) \end{eqnarray}\tag{474.1} $$ 次にIFの$LAT2$での状態確率は、 $$ \begin{eqnarray} \Pr\{\text{IF in }LAT2\}&=&\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\} &=&K_\text{IF,DPF}R_\text{IF}(t) \end{eqnarray}\tag{474.2} $$

$LAT2$から$DPF1$への微小時間間隔$\delta t$での遷移確率は、IFがフォールトによりDPFとなる場合であり、

$$ d\!\Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}=\lambda_\text{IF}\delta t \tag{474.3} $$

従って、状態確率(474.2)と遷移確率(474.3)の積をとりIFの$(t, t+\delta t]$における確率密度を求めれば、 $$ \begin{eqnarray} d\!\Pr\{\text{IF in }LAT2&\text{ at }&t\cap\text{IF down in }(t, t+\delta t]\}\\ &=&d\!\Pr\{\text{IF up at }t\cap\text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\Pr\{\text{IF up at }t\}\Pr\{\text{IF fault prevented}\}\\ &&\cdot d\!\Pr\{\text{IF down in }(t, t+\delta t] | \text{IF up at }t\}\\ &=&K_\text{IF,DPF}R_\text{IF}(t)\lambda_\text{IF}\delta t=K_\text{IF,DPF}f_\text{IF}(t)\delta t \end{eqnarray}\tag{474.4} $$

IFとSM1にはフォールトの生起について独立であるため、各々の確率はかけることができます。よって、 IFの項(474.4)とSM1の項(474.1)の積をとり、$0$から$T_\text{lifetime}$まで積分して時間平均をとると、 $$ \begin{eqnarray} M_\text{PMHF,fsm,P1}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{LAT2 at }t\cap\text{IF fault prevented}\\ &&\cap\ \text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}d\!\Pr\{\text{IF up at }t\cap\text{SM1 down at }t\\ &&\cap\ \text{SM1 fault not detected}\cap\ \text{IF fault prevented}\cap\text{IF down in }(t, t+\delta t]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\text{SM1 down in }[0, t)\cap\text{SM1 fault not detected}\}\\ &&\cdot d\!\Pr\{\text{IF down in }[t, t+\delta t)\cap\text{IF up at }t\cap\text{IF fault prevented}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\text{SM,DPF})F_\text{SM}(t)K_\text{IF,DPF}f_\text{IF}(t)dt\\ &\approx&\frac{1}{2}K_\text{IF,DPF}(1-K_\text{SM,DPF})\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}\\ &=&\frac{1}{2}\lambda_\text{SM,DPF,lat}\lambda_\text{IF,DPF}T_\text{lifetime} \end{eqnarray}\tag{474.5} $$ なお、式変形中に弊社積分公式を使用しています。

(474.5)は図474.2に引用する規格第2版式のPattern 1と正確に一致します。

さらに(474.5)は、図474.3に引用する規格初版第1式のパターン1に相当する部分(図の黄色部分)とも(IF⇒mと読み替えることにより)正確に一致します。

このようにCTMCを用いて、時刻$t$におけるDPF確率密度を0から車両寿命まで積分する方法のほうが、ずっと簡単でわかりやすいです。

なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

前のブログ 次のブログ