|
30 |
6809サブシステム回路図 |
Posts Issued in July, 2019
|
29 |
6809 (2) |
次に、
$ cat header.coe > rom.coe; od -An -v test.o >>rom.coe; echo ';' >> rom.coe
ただし、header.coeは、
memory_initialization_radix=16;
memory_initialization_vector=
これを実行すると、
memory_initialization_radix=16;
memory_initialization_vector=
4f 8e 00 00 a7 80 4c 8c 3e 7f 25 f8 8e 40 00 a7
80 4c 8c 7e 7f 25 f8 8e 80 00 a7 80 4c 8c be 7f
25 f8 20 dd 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
:
:
00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00
00 00 00 00 00 00 00 00 00 00 00 00 00 00 c0 00
;
というテキストファイルのCOEファイルが生成されるので、これをROMデータとしてFPGAに組み込みます。
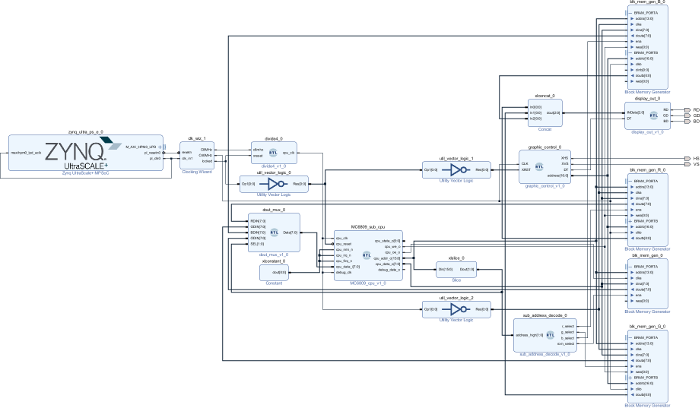
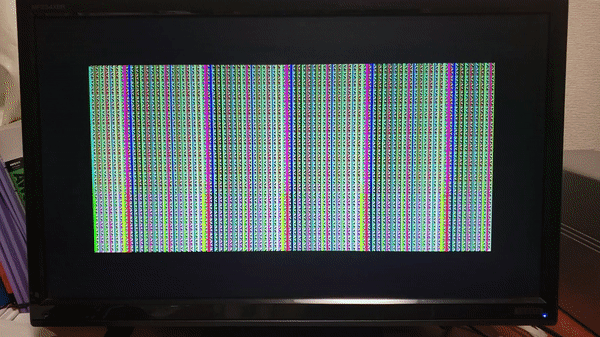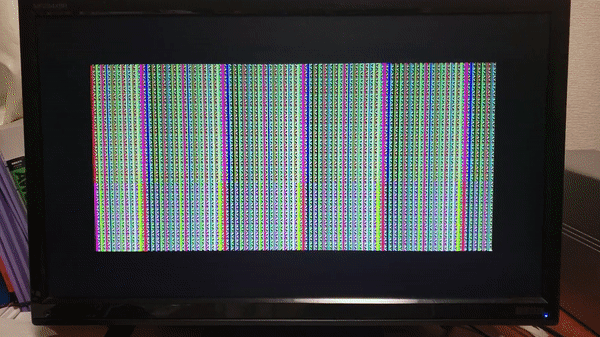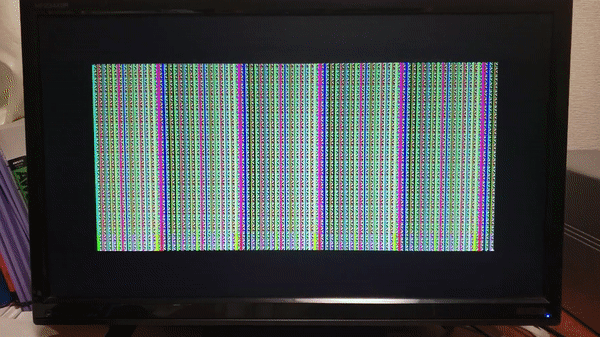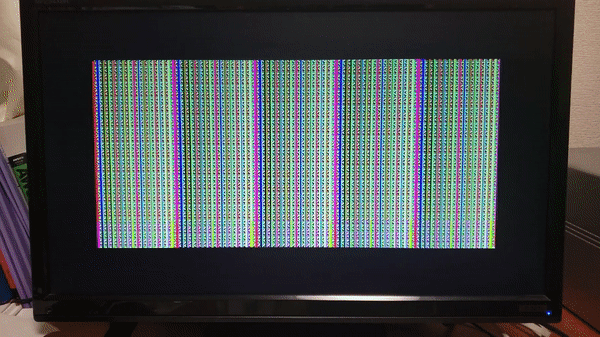
本プログラムはVRAMのアドレスにデータを書き込み、次のアドレスに別のデータを書き込みという処理を繰り返し、VRAMをランダムなデータで埋めるものです。RGBで異なるデータを書き込むために、カラフルな縞模様を表示します。
|
26 |
6809 |
さて、目的はレトロコンピュータの設計ですが、そのために8bit CPUを搭載します。ここでは使用するソフトウェアの関係上6809を取り上げます。入手元はOpen Coresで、VivadoにはRTLとして取り込みます。
https://opencores.org/projects/6809_6309_compatible_core
開発ツールが必要ですが、6809アセンブラを以下から入手します。
https://www.6809.org.uk/asm6809/
画面表示用のサンプルソースファイルをテキストエディタで、
VRAMB equ \$0000
VRAMR equ \$4000
VRAMG equ \$8000
;
start org \$c000
;
clra
l1 ldx #VRAMR
l2 sta ,x+
inca
cmpx #VRAMR+16000-1
blo l2
;
ldx #VRAMG
l3 sta ,x+
inca
cmpx #VRAMG+16000-1
blo l3
;
ldx #VRAMB
l4 sta ,x+
inca
cmpx #VRAMB+16000-1
blo l4
bra l1
;
org \$fffe
fdb start
;
end
として、以下のようにアセンブルします。
asm6809 --bin test.asm -l test.lst -o test.o
以下のアセンブルリストのようにアセンブルされ、合わせてバイナリファイルが生成されます。
0000 VRAMB equ \$0000
4000 VRAMR equ \$4000
8000 VRAMG equ \$8000
;
C000 start org \$c000
;
C000 4F clra
C001 8E0000 l1 ldx #VRAMR
C004 A780 l2 sta ,x+
C006 4C inca
C007 8C3E7F cmpx #VRAMR+16000-1
C00A 25F8 blo l2
;
C00C 8E4000 ldx #VRAMG
C00F A780 l3 sta ,x+
C011 4C inca
C012 8C7E7F cmpx #VRAMG+16000-1
C015 25F8 blo l3
;
C017 8E8000 ldx #VRAMB
C01A A780 l4 sta ,x+
C01C 4C inca
C01D 8CBE7F cmpx #VRAMB+16000-1
C020 25F8 blo l4
C022 20DD bra l1
;
FFFE org \$fffe
FFFE C000 fdb start
;
0000 end
|
25 |
グラフィックタイミング設計 (2) |
SVGAの物理画面のグラフィックタイミングは変更しないので、RTLはタイミングに関してはほとんど変更ありません。以下は元のRTLのグラフィックタイミング定義部分です。
parameter HD=800; // Phyisical Display Timing Horizontal
parameter HFP=40;
parameter HSP=128;
parameter HBP=88;
parameter HO=HFP+HSP+HBP;
parameter HL=HD+HO; // 1056
parameter VD=600; // Phyisical Display Timing Vertical
parameter VFP=1;
parameter VSP=4;
parameter VBP=23;
parameter VO=VFP+VSP+VBP;
parameter VL=VD+VO; // 628
parameter EHD=512; // Embedded Display Timing Horizontal
parameter EVD=512; // Embedded Display Timing Vertical
parameter HW=11;
parameter VW=10;
parameter EHOFF = (HD-EHD)/2; // Embedded Display Offset Horizontal
parameter EVOFF = (VD-EVD)/2; // Embedded Display Offset Vertical
このうち、論理画面のサイズについて、赤字のように修正します。
parameter EHD=640; // Embedded Display Timing Horizontal
parameter EVD=400; // Embedded Display Timing Vertical
parameter HW=12;
しかしながら、Space Invadersと異なり、Xが2の階乗でないため、アドレスカウンタがXとYについてきれいにフィールドで分かれません。従って、水平、垂直カウンタとは別に、VRAMアドレスカウンタを設け、EHD&EVDのディスプレイタイミングでカウントイネーブルをかけます。このようにすれば、表示期間のみアドレスが進み、穴が空く(表示の隣り合うビットが物理的には離れたアドレスに位置する)ことはありません。
さらに、アドレスカウンタを偶数用、奇数用に分け、水平ラインの偶数と奇数でカウンタを進み分けることで、同じアドレスを2回出力することにします。これで縦の2倍拡大が行えます。
実際に動かしてみると、データ表示のビット並びが逆順になっているようです。dual port memoryのA側(CPU側)は8bit幅、B側(ディスプレイ側)は1bit幅で、dual port memoryの内部に8:1のマルチプレクサがあるはずです。表示されたビットの並びが思ったのと逆だったので、アドレス下位3bitを反転することで正しい並びになりました。
|
24 |
グラフィックタイミング設計 |
概略が決定できたので、詳細設計を行います。各パラメータはVGAタイミングのサイトで決定すると、以下の表のようになります。

これに基づき、水平、垂直のタイミングチャートを書くと、以下の図のようになります。
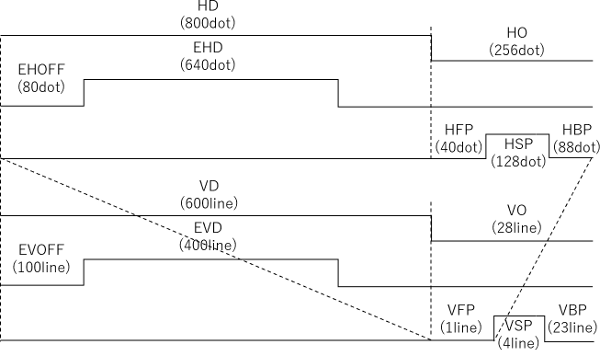
参考のため、HD (Horizontal Display Timing)及びVD (Vertical Display Timing)を示していますが、実際には不要であるため、信号は存在しません。その代わりにEHD (Embedded Horizontal Display Timing)及びEVD (Embedded Vertical Display Timing)を生成し、画面のブランキングを行っています。前稿の物理画面の中に論理画面が存在しますが、論理画面に対するディスプレイタイミングが、このEHD及びEVDとなります。
|
23 |
グラフィックメモリの設計 |
ある目的があり、グラフィックメモリシステムの設計を再度行います。前回設計しているので、パラメータを少々変更するだけで簡単にできそうな気がします。
さて、設計仕様は、昔の8bit PCのVGAをエミュレートするものです。640dotx200dotのRGB各1bitの8色という仕様ですが、横に対して縦のドット数が小さいですね。VGAタイミングのサイトだと640x400というものはあっても、640x200というサイズはありません。
画面が横長に歪であることには理由があり、アドレス空間が16bitであることが関係していると思われます。640x400にすると、RGB各1bit(2^3=8色)だと、メモリに対して8bitアクセスの場合、96,000アドレスとなり、アドレスラインは17bit必要となり、通常の8bitマイコンの16bitアドレス空間として1bit足りません。しかたなく解像度を半分の640x200にすれば、3原色で48,000アドレスとなり、アドレスラインは16bit空間に入ります。
先のFIFOを用いたデザインを再利用して、タイミングだけを変更しようとしたのですが、再検討ついでにFIFOが削除できたので、そのデザインを再利用します。これだと計算が簡単で、dual port memoryで分離されている非同期クロックドメインであるため、ビデオ系のタイミングしか検討する必要がありません。
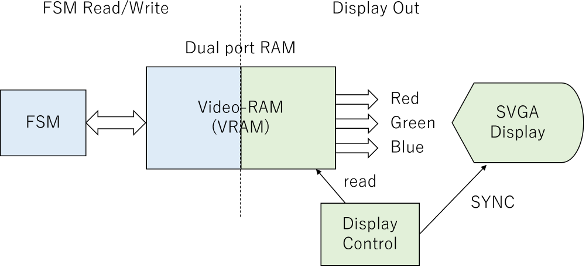
画面構成が640x200なので、それに基づき前回と同じSVGA(800x600)のタイミングで設計することにします。
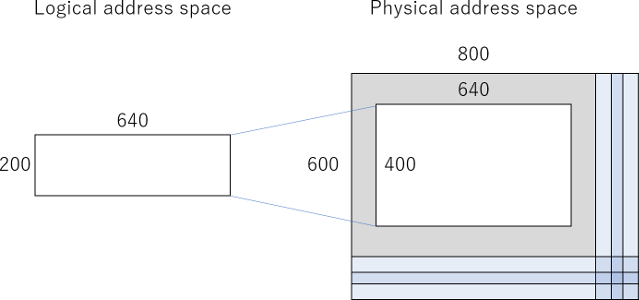
Space Invadersの画面設計を示します。左が論理画面、右が物理画面です。SVGAの物理画面の中央に論理画面を配置し、適宜拡大します。論理画面が256x256と小さいので、縦横2倍の拡大表示を行います。
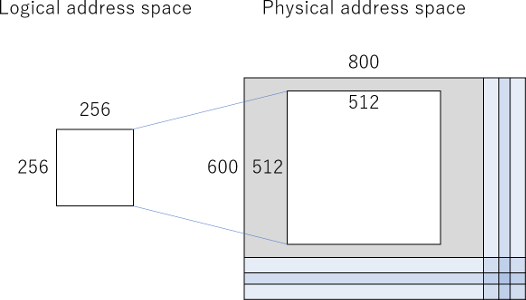
|
22 |
FIFO及びメモリコントローラの除去 |
前稿で設計したグラフィックディスプレイコントローラですが、あとから振り返るとFIFOが無駄であることに気づきました。早速リファクタリングします。
リファクタリング前のクロックドメインが3つあるのに比べて、リファクタリング後は2つに減っています。それだけでなく、FIFOとメモリをリードしてFIFOに入れる回路の2つを削減しています。これはdual port memoryが本来FIFOの役割を果たすためです。
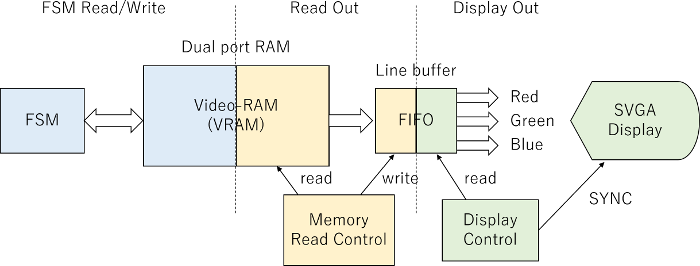
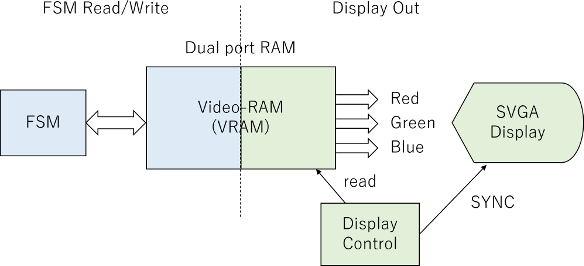
FIFOとメモリ読み出し回路を削減し、メモリ読み出し回路から出ていたメモリアドレスをグラフィックコントローラから出す変更により、問題なくリファクタリングが達成できました。
|
17 |
2nd EditionのPMHF方程式 |
2nd EditionのPMHF方程式は前稿のように、

となっており、Pattern 2及び4に関して、0.5がどこにいったかが謎でした。
ところが、2018年にヨーロッパで実施された機能安全ワークショップでのインテルの資料(恐らくDr. Riccard Marianiの資料)に
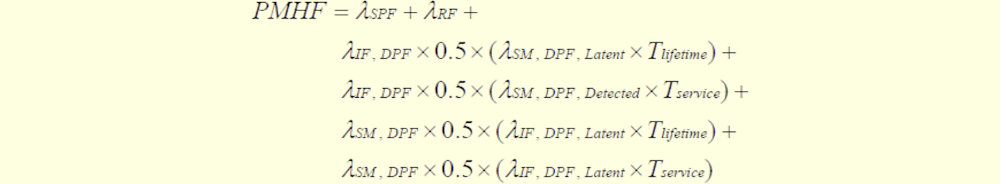
という式が出ており、無くなったことが謎だった0.5が戻っています。どちらかと言えば、こちらのほうが(少しだけ)正しい式です。
結論としては両者とも誤っているのには違いないのですが、謎の部分が無くなったことで、規格式の誤りが明確になりました。誤りの原因は、初期状態において、IFまたはSMのいずれかがアンリペアラブルと固定している点です。実際にこの条件で計算すると、図130.1の式と一致します。
本来は初期状態においてIF、SMの両方ともリペアラブルとしなければなりません。つまり、図109.3の2nd Editionの規格式の誤りは以下の2か所あると思われます。
- パターン2, 4で0.5が消えている件
- こちらのほうが重大ですが、$\img[-1.35em]{/images/withinseminar.png}$
FPGAの設計トライアルとしてスペースインベーダを取り上げたブログ記事を書いてきましたが、最初はAvnetのMicroZedボードで、PMOD-VGAとPMOD-I2Sのインタフェースを購入して、入力はボード上のスイッチを使用していました。
開発がほぼ完了した段階で、AvnetからUltra96 ボードが発売されたので、さっそく購入し移植しようとしましたが、Ultra96はPMODインタフェースを搭載していないため、インタフェースボードを設計せざるを得なくなりました。
そのため、Eagleを使用して、PCBを設計し、さらに格安でPCBを製造するベンダを探しました。中国から送られてきたボードに部品を実装し、ジョイスティックを作成し、ゲームを動作させることができました。
この経緯をQiitaに投稿しました。
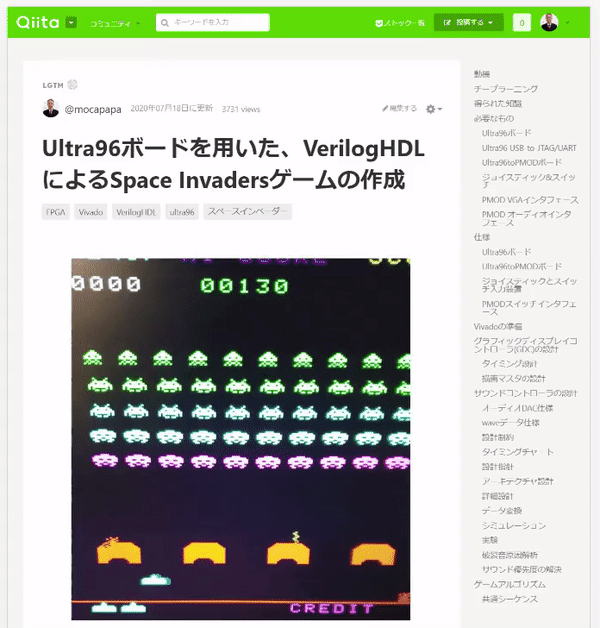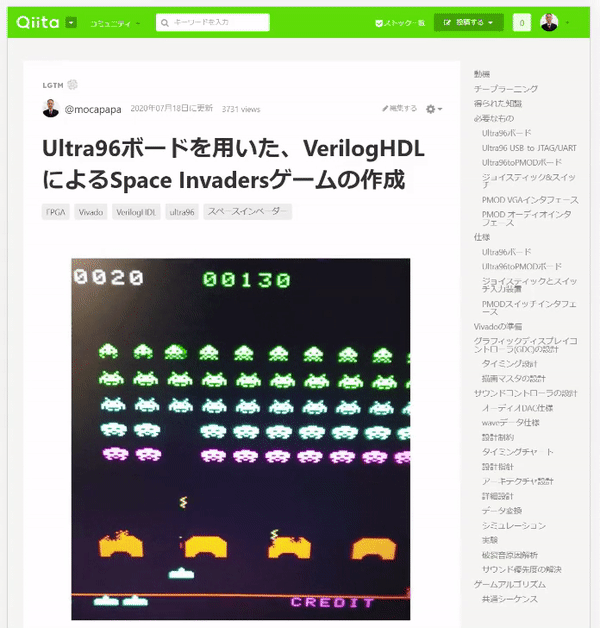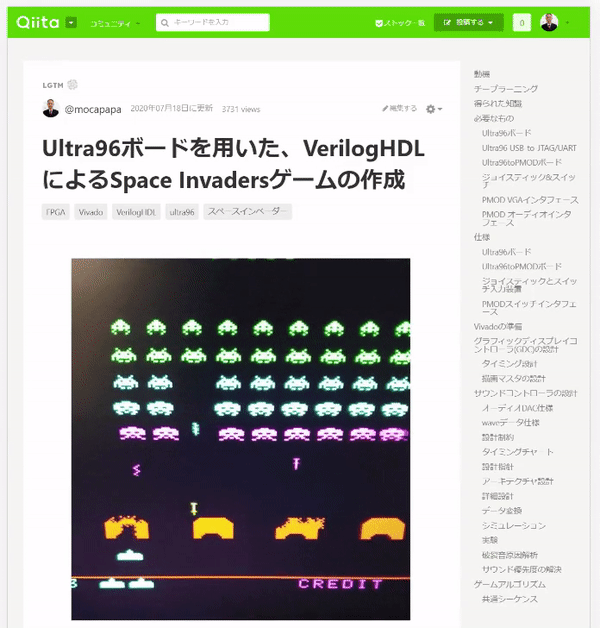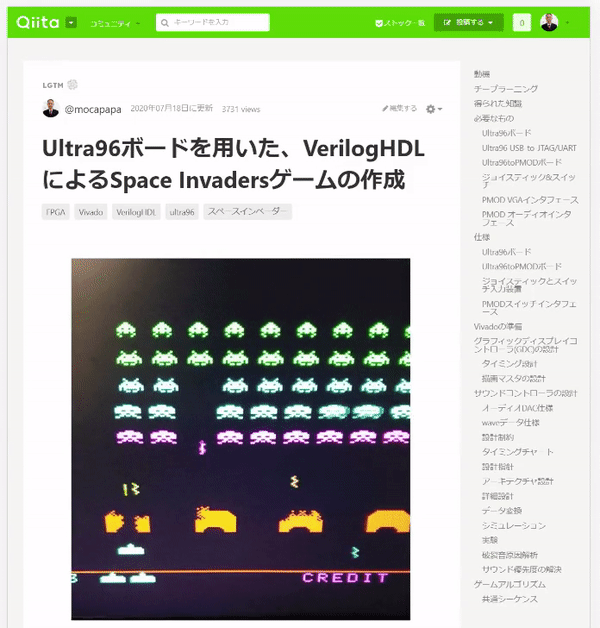
合わせてYouTubeにも上げています。
|
9 |
スタンバイシステムの平均PUD計算 |
さて、前稿の平均PUD計算は簡易的に、冗長システムの確率の1/2として求めましたが、厳密には、
例えば全ての部品を二重化しておき、片方が壊れてももう片方がそれを引き継ぐことができる
という、スタンバイシステムについて平均PUD計算する必要があります。常に両方が稼働する冗長(2重化)と異なり、主系がフォールトしたときに初めて従系が稼働するものです。
IF、SM1からなるサブシステムがあり、IF、SM1の両方ともアンリペアラブルだとします。それぞれの故障率は、$\lambda_\text{IF}$及び$\lambda_\text{SM}$とします。上記のように、IFもSM1も$t=0$から同時に動作している冗長系ではなく、時刻$t$において主系であるIFがダウンし、即座にスタンバイ系であるSM1が引き続いて動作するものとします。
すると、車両寿命$T_\text{lifetime}$における稼働度(Availability)は、IFが$T_\text{lifetime}$までにダウンしないか、あるいは、途中の時刻$t$でダウンしたとしても、そこからSM1が$T_\text{lifetime}$までダウンせずに稼働する確率なので、
$$ A_\text{subsystem}(T_\text{lifetime})=\Pr\{\text{IF not failed at }T_\text{lifetime}\}\\ +\int_0^{T_\text{lifetime}}\Pr\{\text{IF fails in }(t + dt]\cap\text{IF not failed at }t\cap\text{SM not failed in }(T_\text{lifetime}-t]\}\\ =R_\text{IF}(T_\text{lifetime})+\int_0^{T_\text{lifetime}}R_\text{SM}(T_\text{lifetime}-t)F_\text{IF}(t)dt\\ =R_\text{IF}(T_\text{lifetime})+\int_0^{T_\text{lifetime}}e^{-\lambda_\text{SM}(T_\text{lifetime}-t)}\lambda_\text{IF}e^{-\lambda_\text{IF}t}dt\\ =R_\text{IF}(T_\text{lifetime})+\lambda_\text{IF}e^{-\lambda_\text{SM}T_\text{lifetime}}\int_0^{T_\text{lifetime}}e^{-(\lambda_\text{IF}-\lambda_\text{SM})t} dt\\ =R_\text{IF}(T_\text{lifetime})+\lambda_\text{IF}e^{-\lambda_\text{SM}T_\text{lifetime}}\left[\frac{e^{-(\lambda_\text{IF}-\lambda_\text{SM})t}}{-(\lambda_\text{IF}-\lambda_\text{SM})}\right]_0^{T_\text{lifetime}}\\ =R_\text{IF}(T_\text{lifetime})+\lambda_\text{IF}e^{-\lambda_\text{SM}T_\text{lifetime}}\left[\frac{1-e^{-(\lambda_\text{IF}-\lambda_\text{SM})T_\text{lifetime}}}{\lambda_\text{IF}-\lambda_\text{SM}}\right]\\ =R_\text{IF}(T_\text{lifetime})+\frac{\lambda_\text{IF}}{\lambda_\text{IF}-\lambda_\text{SM}}(e^{-\lambda_\text{SM}T_\text{lifetime}}-e^{-\lambda_\text{IF}T_\text{lifetime}})\\ =\img[-1.35em]{/images/withinseminar.png}, \text{ただし、}\lambda_\text{IF}\neq\lambda_\text{SM} \tag{126.1} $$
平均PUDを求めるには不稼働度(Unavailability)の時間平均が知りたいので、$\lambda t\ll 1$の前提で$R(t)=e^{-\lambda t}\approx1-\lambda t+\frac{1}{2}\lambda^2 t^2$と、2次項までMaclaurin展開し、平均PUDを求めると、 $$ \require{cancel} \overline{PUD}=\frac{1}{T_\text{lifetime}}Q_\text{subsystem}(T_\text{lifetime})=\frac{1}{T_\text{lifetime}}\left[1-A_\text{subsystem}(T_\text{lifetime})\right]\\ \approx\frac{1}{\bcancel{T_\text{lifetime}}}\left[\bcancel{1}-(\bcancel{1}-\lambda_\text{IF}\bcancel{T_\text{lifetime}}+\frac{1}{2}{\lambda_\text{IF}}^2 {T_\text{lifetime}}^\bcancel{2})\right]\\ -\frac{1}{\bcancel{T_\text{lifetime}}}\frac{\lambda_\text{IF}}{\lambda_\text{IF}-\lambda_\text{SM}}\left[ (\bcancel{1}-\lambda_\text{SM}\bcancel{T_\text{lifetime}}+\frac{1}{2}{\lambda_\text{SM}}^2 {T_\text{lifetime}}^\bcancel{2})\\ -(\bcancel{1}-\lambda_\text{IF}\bcancel{T_\text{lifetime}}+\frac{1}{2}{\lambda_\text{IF}}^2 {T_\text{lifetime}}^\bcancel{2})\right]\\ =(\lambda_\text{IF}-\frac{1}{2}{\lambda_\text{IF}}^2 T_\text{lifetime})-\frac{\lambda_\text{IF}}{\bcancel{\lambda_\text{IF}-\lambda_\text{SM}}}\left[(\bcancel{\lambda_\text{IF}-\lambda_\text{SM}})-\frac{1}{2}T_\text{lifetime}(\bcancel{\lambda_\text{IF}-\lambda_\text{SM}})(\lambda_\text{IF}+\lambda_\text{SM})\right]\\ =(\bcancel{\lambda_\text{IF}}-\bcancel{\frac{1}{2}{\lambda_\text{IF}}^2 T_\text{lifetime}})-\lambda_\text{IF}\left[\bcancel{1}-\frac{1}{2}T_\text{lifetime}(\bcancel{\lambda_\text{IF}}+\lambda_\text{SM})\right]\\ =\img[-1.35em]{/images/withinseminar.png} \tag{126.2} $$ 以上から、前稿の2重化での簡易計算と完全一致します。
ページ: