SPFMの導出

SPFM、$M_{\mathrm{SPFM}}$に関する規格式を引用し、これを導出します。

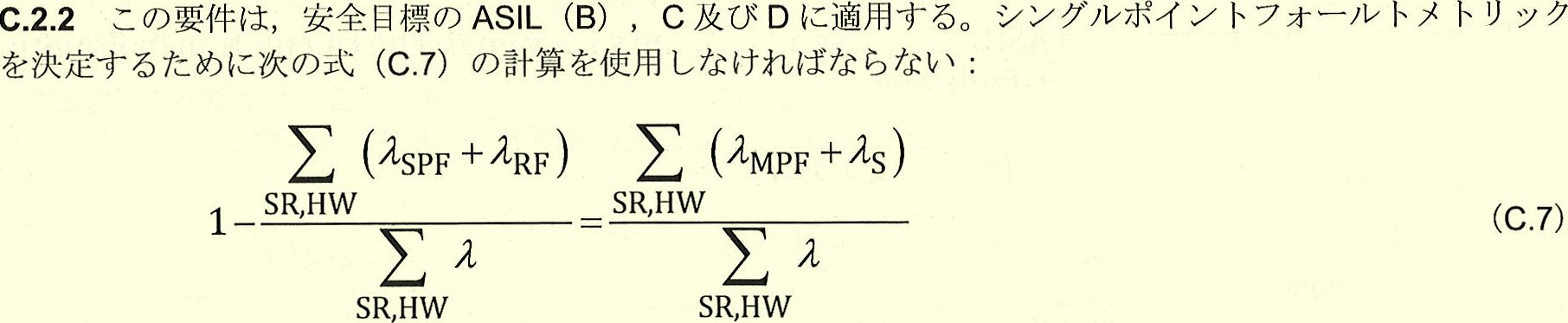
まずレシデュアルフォールト(RF)の故障率の計算式を見てみます。ここでシングルポイントフォールト(SPF)を狭義に使えば、RFのうち、ダイアグノスティックカバレージ(DC)がゼロの時にSPFと等価であるため、SPFもRFも(広義の)RFとして表せることになります。つまり上式分子の$\lambda_{\mathrm{SPF}}+\lambda_{\mathrm{RF}}$は、DC=0の場合を含み、$\lambda_{\mathrm{RF}}$と簡単化できます。

さて、安全関連に関する故障モードが$n$個ある場合に、i番目の(広義の)RFの故障率$\lambda_{\mathrm{RF,}i}$式は、 $$ \lambda_{\mathrm{RF,}i}:=\lambda_{\mathrm{IF,}i}(1-DC_{i})\tag{122.1} $$ と定義されます。この$DC_i$はKパラメータで書けば、 $$ DC_i=K_{\mathrm{IF,FMC,RF,}i} $$ となり、1st SMがIFに対して、IFがSG侵害を抑止する割合を表します。(122.1)の両辺の総和を取れば、 $$ \sum_{i=1}^n\lambda_{\mathrm{RF,}i}=\sum_{i=1}^n\lambda_{\mathrm{IF,}i}(1-DC_{i}) =\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_{i} \tag{122.2} $$ よって、 $$ \sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_{i}=\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{RF,}i} \tag{122.3} $$ ここで、各々のSMにより防御される、IFの故障率によるDCの加重平均を次のように定義し、 $$ \overline{DC}:=\frac{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_i}{\sum_{i=1}^n\lambda_i} \tag{122.4} $$ (122.3)を(122.4)の分子に代入すれば、 $$ (122.4)=\frac{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{RF,}i}}{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}} =1-\frac{\sum_{i=1}^n\lambda_{\mathrm{RF,}i}}{\sum_{i=1}^n\lambda_i} \tag{122.4} $$ これと(C.7)を比較すれば、 $$ M_{\mathrm{SPFM}}=\overline{DC} $$ となるため、SPFMは$\img[-1.35em]{/images/withinseminar.png}$

前のブログ 次のブログ