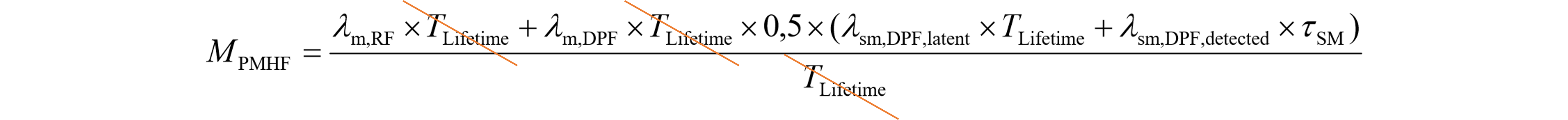DPF1の再計算
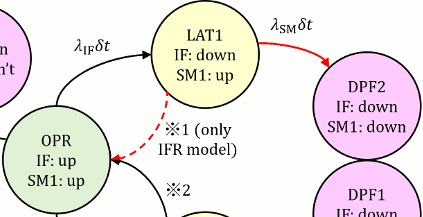
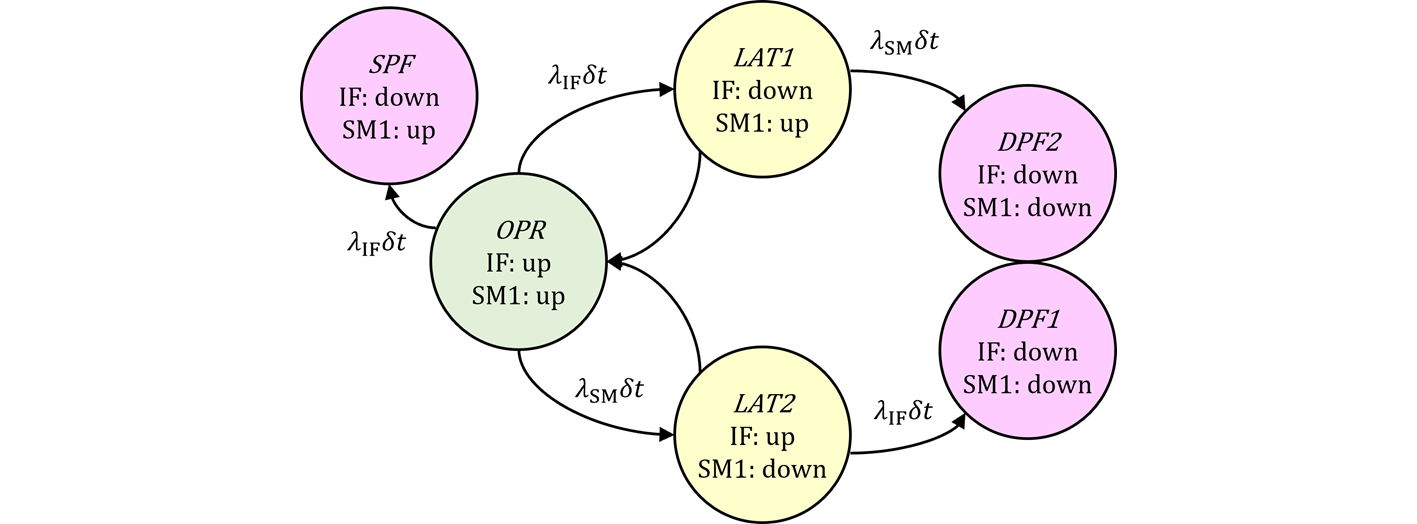
ところがこのケース2.の場合は、(無関係と思われた)DPF1について再計算する必要があります。その理由は、IFの条件がアンリペアラブルからリペアラブルに変更され、リペアすることによりOPRの状態確率が上がり、結果としてDPF1の確率が下がるためです。図107.1に図104.1を再掲します。LAT2においてはIF=upであったのに対し、DPF1においてはIF=downとなります。
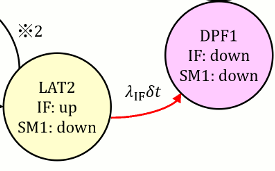 図107.1 CTMCにおいてLAT2⇒DPF1の遷移
図107.1 CTMCにおいてLAT2⇒DPF1の遷移
(104.1)を参考に、IFRモデルに変更します。
$$
\begin{eqnarray}
\overline{q_{\mathrm{DPF1,IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF1\ at\ }T_\text{lifetime}\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\
& &\cdot\Pr\{\mathrm{LAT2}\mathrm{\ at\ }t\}
\end{eqnarray}
\tag{107.1}
$$
ここまでは(104.1)と同じです。LAT2はIFの稼働状態でかつSM1の不稼働状態であるから、
$$
\Pr\{\mathrm{LAT2\ at\ }t\}=\Pr\{\mathrm{IF\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\}\tag{107.2}
$$
IFとSM1の稼働状態は独立事象であり、IFRモデルではIF、SM1共にリペアラブルであることから、(107.2)は
$$
(107.2)=\Pr\{\mathrm{IF^R\ up\ at\ }t\}\Pr\{\mathrm{SM\ down\ at\ }t\}\\
=A_{\mathrm{IF}}(t)Q_{\mathrm{SM}}(t)\tag{107.3}
$$
と書けるように思われますが誤りです。IFのフォールトはVSG non preventableとVSG preventableに分けられるので、分配則より、
$$
\Pr\{\mathrm{IF\ up\ at\ }t\}=\Pr\{\left(\overline{\text{IF preventable}}\cup\text{IF preventable}\right)\cap\mathrm{IF\ up\ at\ }t\}\\
=\Pr\{\left(\overline{\text{IF preventable}}\cap\mathrm{\color{red}{IF^U}\ up\ at\ }t\right)\cup\left(\text{IF preventable}\cap\mathrm{IF^R\ up\ at\ }t\right)\}\tag{107.4}
$$
となります。$\mathrm{\color{red}{IF^U}}$に注意してください。$\overline{\text{IF preventable}}$とはSM1によりVSG抑止できないことを意味し、修理は不可能であるため、その部分のIFはアンリペアラブルとなります。
ちなみに、この部分の確率はSMの状態によらずVSGとなるため、本質的にはSPFに入りそうですが、形式的にはSMがdownしているときのIFのフォールトなので、本稿ではDPFに入れます。なお、SPFに分類してもDPFに分類しても最終的には確率の総和を取るため、結果に変わりはありません。
従って、(107.4)のIFの前半がアンリペアラブル、後半がリペアラブルなので、(107.4)は、
$$
\require{cancel}
\Pr\{\mathrm{IF\ up\ at\ }t\}=(1-K_{\text{IF,RF}})R_\text{IF}(t)+K_{\text{IF,RF}}A_\text{IF}(t)\\
(新規追加)=(1-\bcancel{K_{\text{IF,RF}}})R_\text{IF}(t)+K_{\text{IF,RF}}(\bcancel{1}-K_{\text{IF,MPF}})R_\text{IF}(t)+K_{\text{IF,RF}}K_{\text{IF,MPF}}R_\text{IF}(u)\\
=(1-K_{\text{IF,RF}}K_{\text{IF,MPF}})R_\text{IF}(t)+K_{\text{IF,RF}}K_{\text{IF,MPF}}R_\text{IF}(u),
ただし、u:=t\bmod\tau
\tag{107.5}
$$
となるため、(107.2)は(107.5)を用いて、
$$
\Pr\{\mathrm{LAT2\ at\ }t\}=\Pr\{\mathrm{IF\ up\ at\ }t\}\Pr\{\mathrm{SM\ down\ at\ }t\}\\
=\left[(1-K_{\text{IF,RF}})R_\text{IF}(t)+K_{\text{IF,RF}}A_\text{IF}(t)\right]Q_{\mathrm{SM}}(t)\\
(新規追加)=\left[(1-K_{\text{IF,RF}}K_{\text{IF,MPF}})R_\text{IF}(t)+K_{\text{IF,RF}}K_{\text{IF,MPF}}R_\text{IF}(u)\right]Q_{\mathrm{SM}}(t),\\
ただし、u:=t\bmod\tau
\tag{107.6}
$$
と書けます。
さらに、(107.1)の右辺積分中の条件付き確率式に、独立条件付き確率式(103.4)、及び微小故障条件付き確率式(66.8)を用いれば、DPF時の2つ目のフォールトはIF、SM1共にアンリペアラブルとなるため、
$$
\require{cancel}
\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\
=\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\cap\bcancel{\mathrm{SM\ down\ at\ }t}\}\\
=\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}=\lambda_{\mathrm{IF}}dt\tag{107.7}
$$
となります。
よって、(107.1)に(107.7)、(107.6)を適用した上で、PUA(59.8)、PA(59.7)、故障率(66.6)及び弊社積分公式(60.1)及び(60.2)を用いれば、
$$
\begin{eqnarray}
\overline{q_{\mathrm{DPF1,IFR}}}&=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt+\frac{K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)A_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt\\
&=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)f_{\mathrm{IF}}(t)dt+\frac{K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)q_{\mathrm{IF}}(t)dt\\
&=&\frac{1-K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_{\mathrm{SM,MPF}})F_{\mathrm{SM}}(t)+K_{\mathrm{SM,MPF}}F_{\mathrm{SM}}(u)]f_{\mathrm{IF}}(t)dt\\
& &+\frac{K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}[(1-K_{\mathrm{SM,MPF}})F_{\mathrm{SM}}(t)+K_{\mathrm{SM,MPF}}F_{\mathrm{SM}}(u)]\\
& &\cdot\left[(1-K_{\mathrm{IF,MPF}})f_{\mathrm{IF}}(t)+K_{\mathrm{IF,MPF}}f_{\mathrm{IF}}(u)\right]dt,\\
& &ただし、u:=t\bmod\tau\\
&\approx&\frac{1-K_{\mathrm{IF,RF}}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\
& &+\frac{K_{\mathrm{IF,RF}}}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-
K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau]\\
&=&(1-K_{\mathrm{IF,RF}})\alpha+K_{\mathrm{IF,RF}}\beta,\\
\end{eqnarray}
\tag{107.8}
$$
$$
ただし、\begin{cases}
\begin{eqnarray}
\alpha&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\
\beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau]\\
K_{\mathrm{MPF}}&:=&K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}}\\
\end{eqnarray}
\end{cases}
$$
となります。
(2021年1月新規追加)これを整理すれば、
$$
\begin{eqnarray}
(107.8)&=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-
K_{\mathrm{MPF2}})T_\text{lifetime}+K_{\mathrm{MPF2}}\tau]\\
& &ただし、K_{\mathrm{MPF2}}:=K_{\mathrm{IF,RF}}K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,RF}}K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}}\\
\end{eqnarray}
\tag{107.9}
$$
となります。これは(107.6)の新規追加式を積分した結果と同一になります。
RAMS 2020においてPMHF式の論文発表が終了したため、本記事を開示します。
 前のブログ
次のブログ
前のブログ
次のブログ