LAT2⇒DPF1の平均PUDの計算

次にLAT2からDPF1となる平均PUDを計算します。時刻$t$でLAT2においてはIF=upであったのに対し、$t+dt$までの間にIFにフォールトが起き、IF=downとなると同時にDPF1に移行します。

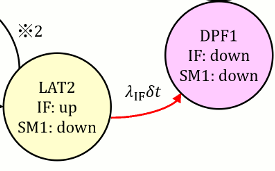
CTMCの平均PUD基本式(101.5)について、条件付き確率の公式を用いて、 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF1,IFU}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF1\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2}\mathrm{\ at\ }t\} \end{eqnarray} \tag{104.1} $$ ここで、LAT2はIFが稼働、SM1が不稼働状態であるから、 $$ \Pr\{\mathrm{LAT2\ at\ }t\}=\Pr\{\mathrm{IF\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\}\tag{104.2} $$ IFとSM1の稼働状態は独立事象で、IFはアンリペアラブル、SM1はリペアラブルであることから、(104.2)は $$ \Pr\{\mathrm{LAT2\ at\ }t\}=\Pr\{\mathrm{IF^U\ up\ at\ }t\}\Pr\{\mathrm{SM\ down\ at\ }t\}\\=R_{\mathrm{IF}}(t)Q_{\mathrm{SM}}(t)\tag{104.3} $$ と書けます。

さらに、(104.1)の右辺積分中の条件付き確率式に(104.2)、独立条件付き確率式(103.4)、及び微小故障条件付き確率式(66.8)を適用すれば、IFはアンリペアラブルであるため、 $$ \require{cancel} \Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\cap\bcancel{\mathrm{SM\ down\ at\ }t}\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}=\lambda_{\mathrm{IF}}dt\tag{104.4} $$ よって、(104.1)に(104.4)、(104.3)を用いた上で、PUA(59.8)、故障率(66.6)、及び弊社積分公式を適用すれば、 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF1,IFU}}}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\text{SM}(t)f_\mathrm{IF}(t)dt\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_{\mathrm{SM,MPF}})F_{\mathrm{SM}}(t)+K_{\mathrm{SM,MPF}}F_{\mathrm{SM}}(u)\right]f_{\mathrm{IF}}(t)dt,\\ & &ただし、u:=t\bmod\tau\\ &\approx&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}\left[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau\right]\\ &=&\alpha,\\ & & ただし、\alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau] \end{eqnarray} \tag{104.5} $$ よって、(103.7)及び(104.5)より、 $$ \begin{eqnarray} M_{\mathrm{PMHF}}&=&\overline{q_{\mathrm{SPF,IFU}}}+\overline{q_{\mathrm{DPF1,IFU}}}\\ &=&(1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}+\frac{1}{2}K_{\mathrm{IF,RF}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ &=&(1-K_{\mathrm{IF,RF}})\lambda_{\mathrm{IF}}+K_{\mathrm{IF,RF}}\alpha \end{eqnarray} \tag{104.6} $$ であり、さらに基本故障率及びパラメータにより各条件を含む故障率が記述でき、 $$ \begin{cases} \begin{eqnarray} \lambda_\text{IF,RF}&:=&(1-K_\text{IF,RF})\lambda_\text{IF}\\ \lambda_\text{IF,DPF}&:=&K_\text{IF,RF}\lambda_\text{IF}\\ \lambda_\text{SM,DPF,lat}&:=&(1-K_\text{SM,MPF})\lambda_\text{SM}\\ \lambda_\text{SM,DPF,det}&:=&K_\text{SM,MPF}\lambda_\text{SM} \end{eqnarray} \end{cases} \tag{104.7} $$ を用いて $$ (104.6)=\lambda_{\mathrm{IF,RF}}+\frac{1}{2}\lambda_{\mathrm{IF,DPF}} (\lambda_{\mathrm{SM,DPF,lat}}T_\text{lifetime}+\lambda_{\mathrm{SM,DPF,det}}\tau)\tag{104.8} $$ と書きなおせるため、(104.8)は次の図104.2に示す、ISO 26262 1st edition Part 10の最初のPMHF式、すなわちSM1に引き続きIFがフォールトすると(誤って)書かれている式と、(IF⇒Mと読み替えることにより)完全に一致します。

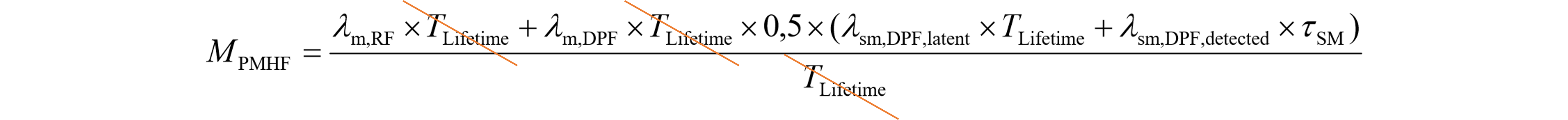
RAMS 2020においてPMHF式の論文発表が終了したため、本記事を開示します。

前のブログ 次のブログ