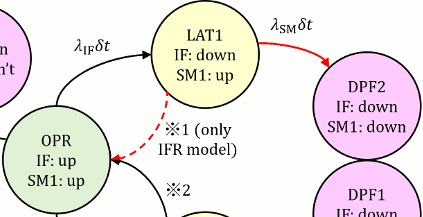
2. LAT1において、検出周期内ではSM1のフォールトに応じて確率的にDPF2に遷移する。一方検出周期の最後で、検出されたIFのフォールトはリペアされOPRに戻る場合(IFRモデル)

ケース2.の場合の計算です。2nd Editionの中にPattern4が以下の図のように書かれています。IFが先にフォールトし、それが検出される場合についてはリペアされると推測され、Pattern4はこのケース2.の場合であると考えられます。

(日本語訳)IFのフォールトは軽減され、SM1によって通知されます。フォールトの露出時間は、ドライバーが車両を修理に持ち込むのに必要な予想時間と見なされます。

これが成立するのは、(規格には書かれていませんが1)SM1にIFの代替機能がある場合に限られます。それが無い場合は前稿のIFUモデルに対応します。それがある場合はIFRモデルに対応します。2nd EditionではPattern3及び4が追加され、IFRモデルを前提としており、本ケース2.が相当すると考えます。

前ページの(105.1)のIFUモデルをIFRモデルに変更します。 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF2,IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF2\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT1\ at\ }t\cap\mathrm{SM\ down\ in\ }(t, t+dt)\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT1\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT1\ at\ }t\} \end{eqnarray} \tag{106.1} $$

ここで、LAT1はIFの不稼働状態でかつSM1によりVSGは抑止されるがSM2により検出されず、かつSM1の稼働状態であるから、 $$ \Pr\{\mathrm{LAT1\ at\ }t\}=\Pr\{\mathrm{IF\ down\ at\ }t\cap\text{VSG of IF preventable}\cap\mathrm{SM\ up\ at\ }t\}\tag{106.1} $$ IFとSM1の稼働状態は独立事象であり、IF、SM1は共にリペアラブルです。前稿にならいリペアラブルなIFを$\mathrm{IF^R}$と書くことにします。

SM1のVSG prevent能力はアーキテクチャ的に決定されるため、他の事象とは独立と考え、$K_\text{IF,RF}$(101.3)を用いると、(106.1)は $$ \Pr\{\mathrm{LAT1\ at\ }t\}=\Pr\{\mathrm{IF^R\ down\ at\ }t\}\Pr\{\text{VSG of IF preventable}\}\Pr\{\mathrm{SM\ up\ at\ }t\}\\ =K_{\mathrm{IF,RF}}Q_{\mathrm{IF}}(t)A_{\mathrm{SM}}(t)\tag{106.2} $$ と書けます。

さらに、(105.1)の右辺積分中の条件付き確率式に(106.1)、独立条件付き確率式(103.4)、及び微小故障条件付き確率式(66.8)を用い、DPF時の2つ目のフォールトはIF、SM1共にアンリペアラブルとなるため、 $$ \require{cancel} \Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT1\ at\ }t\}\\ =\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{SM\ up\ at\ }t\cap\bcancel{\mathrm{IF^R\ down\ at\ }t}\cap\bcancel{\text{VSG of IF preventable}}\}\\ =\Pr\{\mathrm{SM\ down\ in\ }(t, t+dt]\ |\ \mathrm{SM\ up\ at\ }t\}=\lambda_{\mathrm{SM}}dt\tag{106.3} $$ よって、(105.1)に(106.3)、(106.2)を適用した上で、PUA(59.8)、PA(59.7)、故障率(66.6)及び弊社積分公式を用いれば、 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF2, IFR}}}&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}K_{\mathrm{IF,RF}}Q_{\mathrm{IF}}(t)A_{\mathrm{SM}}(t)\lambda_{\mathrm{SM}}dt\\ &=&\frac{K_{\mathrm{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_{\mathrm{IF,MPF}})F_{\mathrm{IF}}(t)+K_{\mathrm{IF,MPF}}F_{\mathrm{IF}}(u)\right]\\ & &\cdot\left[(1-K_\text{SM,MPF})f_\text{SM}(t)+K_\text{SM,MPF}f_\text{SM}(u)\right]dt,\\ & &ただし、u:=t\bmod\tau\\ &\approx&\frac{K_{\mathrm{IF,RF}}}{2}\lambda_{\mathrm{SM}}\lambda_{\mathrm{IF}}\left[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau\right], \\ & &ただし、K_{\mathrm{MPF}}:=K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}}\\ &=&K_{\mathrm{IF,RF}}\beta, \\ & &ただし、\beta:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau] \end{eqnarray} \tag{106.4} $$

RAMS 2020においてPMHF式の論文発表が終了したため、本記事を開示します。

前のブログ 次のブログ