|
13 |
$M_\text{PMHF}$の計算 (8) |
IFUモデル LAT2分離
IFUモデルのLAT2ステートにおいて、IFのアンプリベンタブル(VSG抑止不可)な部分にフォールトが起きた場合、そのフォールトはSMのup/down状態に依存しないため、本質的には広義のSPF(SMがあるので狭義ではRF)ですが、形式的にはSMのフォールトに引き続いて起きるためDPFとしました(#104)。
前稿(#102~#108)のPMHF導出においては、DPFとして扱いましたが、「$M_{\mathrm{PMHF}}$の計算(2)」のMarkov chain図を変更し、LAT2からDPF1への遷移(2)を分離して、DPF1への遷移(2a)とSPF1への遷移(2b)とに分離します(図221.1の赤矢印)。
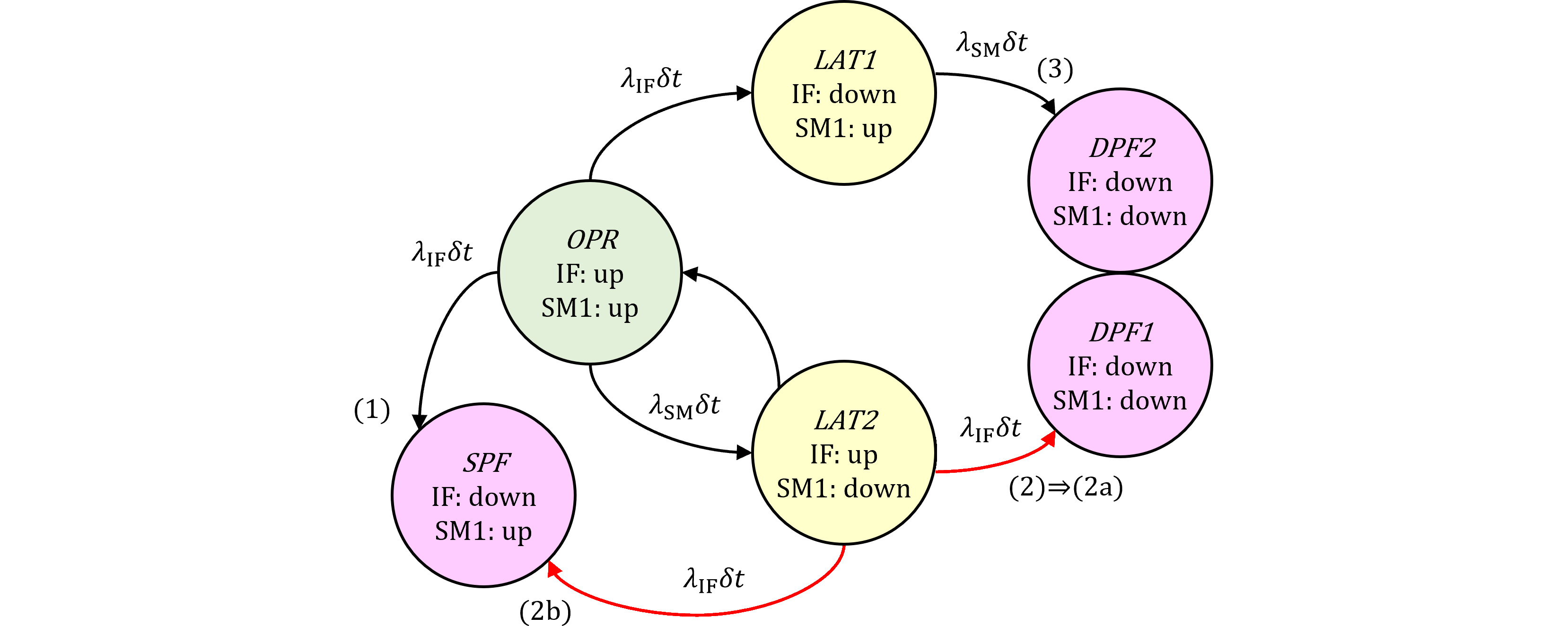
図221.1の(1)、(3)の確率微分方程式は変わりません。まず(2a)のDPF1方向への確率積分は、 $$ \begin{eqnarray} \overline{q_{\mathrm{DPF1,IFU}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{DPF1\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{IF^U\ down\ in\ }(t, t+dt]\\ & &\cap\mathrm{VSG\ of\ IF\ preventable}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2\ at\ }t\}\Pr\{\mathrm{VSG\ of\ IF\ preventable}\} \end{eqnarray} \tag{221.1} $$ ここで(104.2)、(104.3)より、 $$ \Pr\{\mathrm{LAT2\ at\ }t\}=\Pr\{\mathrm{IF^U\ up\ at\ }t\cap\mathrm{SM\ down\ at\ }t\}\\ =\Pr\{\mathrm{IF^U\ up\ at\ }t\}\Pr\{\mathrm{SM\ down\ at\ }t\}\\=R_{\mathrm{IF}}(t)Q_{\mathrm{SM}}(t)\tag{221.2} $$ (104.4)より、 $$ \Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ =\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{IF^U\ up\ at\ }t\}=\lambda_{\mathrm{IF}}dt\tag{221.3} $$ (221.2)、(221.3)を(221.1)に用いれば、 $$ \overline{q_{\mathrm{DPF1,IFU}}}=\frac{K_{\text{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt \tag{221.4} $$ ゆえに、(104.5)の結果を利用すれば、(2a)は、 $$ (221.4)=K_{\text{IF,RF}}\alpha\tag{221.5} $$
次に(2b)のSPF方向への確率積分は、 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF(2b),IFU}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF(2b)\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{IF^U\ down\ in\ }(t, t+dt]\\ & &\cap\overline{\mathrm{VSG\ of\ IF\ preventable}}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2\ at\ }t\}\Pr\{\overline{\mathrm{VSG\ of\ IF\ preventable}}\} \end{eqnarray} \tag{221.6} $$ 同様に(221.2)、(221.3)を用いれば、 $$ \overline{q_{\mathrm{SPF(2b),IFU}}}=\frac{1-K_{\text{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt \tag{221.7} $$ ゆえに、(104.5)の結果を利用すれば、(2b)は、 $$ (221.7)=(1-K_{\text{IF,RF}})\alpha\tag{221.8} $$
IFUモデル SPF統合
$\dagger$「IFUモデルのLAT2において、IFのアンプリベンタブル部分にフォールトが起きた場合」について、SPFへの遷移(2b)とDPF1への遷移(2a)の確率積分を行いました。今度はSPFへの確率積分を統合します。図221.1において(1)と(2b)はいずれもSPFとして扱い、これをSPF統合と呼びます。
- LAT2統合 --- $\dagger$の場合、SPFへの遷移(2b)は本質的にSPFであるが、形式的にSMのフォールトに引き続くDPF(2)=(2a)+(2b)として計算、#103~#105の議論
- LAT2分離 --- $\dagger$の場合、LAT2からの遷移(2)を、SPFへの遷移(2b)とDPF1への遷移(2a)に分離、本稿の議論
- SPF統合 --- $\dagger$の場合、LAT2からSPFへの遷移(2b)と、元のOPRからSPFへの遷移(1)を統合、LAT2分離によりそれぞれ求めた確率の組み合わせを変更、本稿の議論
- SPF/DPF統合 --- $\dagger$の場合、SPF統合に加えて、DPF1とDPF2は同じ状態であるため、DPFも統合
それぞれの方式のPMHF式と、参考にPMHF規格式を比較すると、表221.1のようになります。前稿からの変化部分を黄色で示しています。
| (1)SPF | (2)DPF1 | (3)DPF2 | ||
|---|---|---|---|---|
| LAT2統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$ (103.7) |
$\alpha$ (104.5) |
$K_\text{IF,RF}\alpha$ (105.5) |
|
| 規格式1(1)+(2)$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\alpha$ (104.6) |
|||
| 規格式3(1)+(2)+(3)$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+2K_\text{IF,RF}\alpha$ | |||
| (1)SPF | (2b)SPF' | (2a)DPF1 | (3)DPF2 | |
| LAT2分離 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$ | $(1-K_\text{IF,RF})\alpha$ (221.8) |
$K_\text{IF,RF}\alpha$ (221.5) |
$K_\text{IF,RF}\alpha$ |
| (1)+(2b)SPF | (2a)DPF1 | (3)DPF2 | ||
| SPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $K_\text{IF,RF}\alpha$ | $K_\text{IF,RF}\alpha$ | |
| SPF/DPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $2K_\text{IF,RF}\alpha$ | ||
ただし$\alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1- K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]$
以上より、一般式は、 $$M_\text{PMHF}=(1-K_\text{IF,RF})\lambda_\text{IF}+2K_\text{IF,RF}\alpha\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{SM,MPF})T_\text{lifetime}+K_\text{SM,MPF}\tau\right]\tag{221.9}$$
SPF統合は、SPFのPMHFがRFの定義そのままという、非常に単純な式となっています。従って、#103のSPFのPMHF式や1st editionの規格式が複雑なのは、形式上のDPFをSPFから差し引いたためと言えます。また、DPF1とDPF2はルートが異なるのに同一の確率となっているのが少々驚きです。
$\dagger$規格式1: 規格第1版 Part 10-8.3.3の第1式(ブログの図104.2)の条件=IFが後にフォールトする場合。DPF2はSMが後にフォールトする場合なので対象外
$\dagger$規格式3: 規格第1版 Part 10-8.3.3の第3式(ブログの図105.2)の条件=IF, SMのフォールトの順を問わない場合
RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。

Leave a Comment