 |
24 |
ASILデコンポジション論文ward2012 (3) |
 |
論文ward2012$\dagger$の続きです。具体例が参考になるので、具体的な要求に従って検討していきます。
Below are some examples illustrating common misuse of requirements decomposition.
以下に、要件分解の一般的な誤用を説明するいくつかの例を示します。
最初の例はESL (Electronic Steering Lock)です。ESLとは、盗難防止装置であるステアリングロックを電子的に行うもので、停止状態(=車速がある速度以下)で、一定の条件でステアリングを回転させないようにカンヌキをかけるシステムです。図300.1はESLの初期アーキテクチャです。

この初期アーキテクチャのSGは以下のようです。
SG01: When the vehicle is being driven, the steering lock shall not engage unintentionally [ASIL D].
SG01: 車両の運転中は、ステアリングロックが意図せずに作動してはならない[ASIL D]。
前述のように、走行中にESLが働くと大変なことになります。SG中の意図せずというのは、故障した場合と読み替えることができます。このSGに従い、次の初期TSRを導出しました。
REQ 22: The Microcontroller shall activate the drive signal to the bridge drive when “lock” conditions are received over the CAN bus. [ASIL D]
REQ 22: 「ロック」状態がCANバスで受信された場合、マイクロコントローラはブリッジドライブへのドライブ信号をアクティブにしなければならない。[ASIL D]
が、これではASIL-Dを担保できないでしょう。なぜなら、マイクロコントローラの単一故障で走行中にステアリングロックする可能性が高いためです。そのため本論文では、初期安全要求REQ 22をREQ 22.1とREQ 22.2に分解しています。
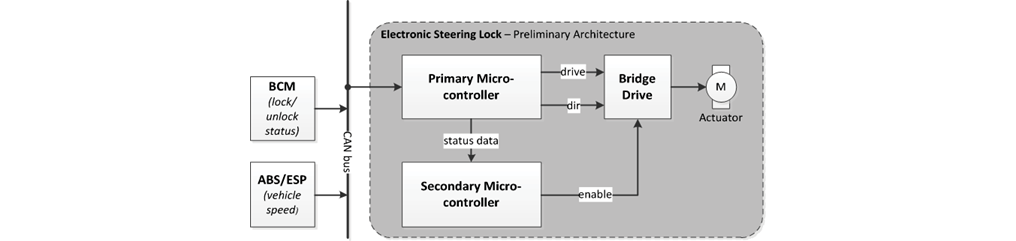
次のREQ 22.1と、
REQ 22.1: The primary microcontroller shall activate the drive signal to the bridge drive when a “lock” command is received over the CAN bus. [ASIL B(D)]
REQ 22.1. プライマリ・マイコンは、CANバス上で「ロック」コマンドを受信すると、ブリッジ・ドライブへのドライブ信号をアクティブにしなければならない。[ASIL B(D)]
次のREQ 22.2
REQ 22.2: The secondary microcontroller shall activate the enable signal to the bridge drive when the vehicle speed received over the CAN bus indicates that lock conditions are plausible (i.e. the vehicle is stationary). [ASIL B(D)]
REQ 22.2. セカンダリマイコンは、CANバスを介して受信した車速がロック状態が妥当であることを示した場合(すなわち、車両が静止している場合)に、ブリッジドライブへのイネーブル信号をアクティブにしなければならない。[ASIL B(D)]
ですが、この分解には問題があります。現実にも見られる例ですが、論文中にも、
there is a common-cause failure (the CAN reception; element’s sub-parts and software) which could cause both REQ 22.1 and REQ 22.2 to fail simultaneously.
REQ 22.1 と REQ 22.2 の両方が同時に失敗する原因となる共通の障害(CAN 受信;エレメントのサブパーツとソフトウェア)がある
とあるように、分解されたエレメント同士の独立性に違反しています。すなわち、ASILデコンポジションとして成立していません。
※このように述べると全くダメなようですが、実は成立するやり方があります。初期安全要求をCANをはずすようにすれば、独立性に違反しませんし、ASILデコンポジションはハードウェアに関しては無意味であるため、本来マイコンのみを含むようにするのが良いのです。この辺りはASILデコンポジションのテクニックやノウハウに関するところとなります。
$\dagger$Ward, D. D., & Crozier, S. E. (2012). The uses and abuses of ASIL decomposition in ISO 26262. 7th IET International Conference on System Safety, Incorporating the Cyber Security Conference 2012.
