|
27 |
ISO 26262のFTAに関する論文 (10) |
参照論文の問題点を挙げていけば、きりがないようです。
図210.1は前稿の事象E2である、AがRFとなった後にBがSPF/RFとなる場合のFTです。
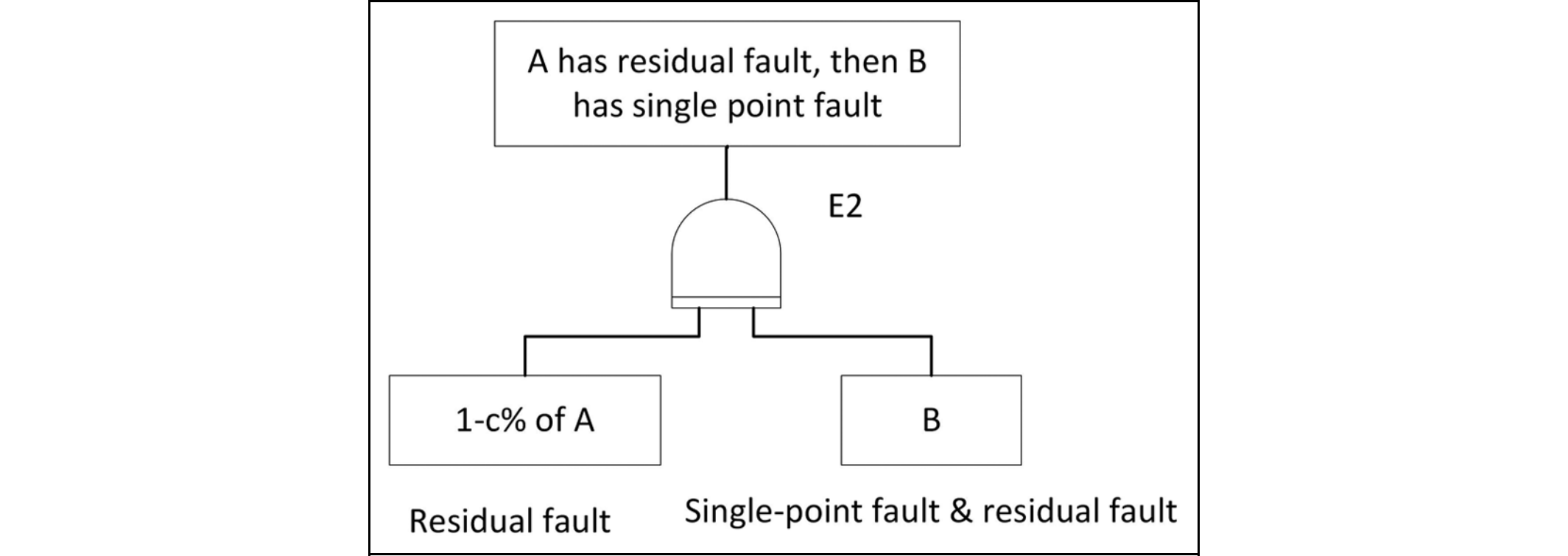
図210.2は事象E2のマルコフチェイン図です。

そもそも前述のようにE2事象自体がおかしいのですが、それを無視して考えます。さらに子細に検討すると変なところが目につきます。例えば、マルコフ状態遷移は、
- 00 E2が起きない、00が起きる確率を$P_{00}(t)$とする。
- 1 中間状態(??)、1が起きる確率を$P_{1}(t)$とする。
- 11 E2が起きる、11が起きる確率を$P_{11}(t)$とする。
と遷移するようです。ここで、E2は起きるか起きないかなので、中間はありません。事象とその確率分布は別の話で、それが分離できていないのかもしれません。コイントスの例を挙げれば、事象は表が出るか出ないか(裏が出るか)のどちらか一方です。ただ表が出るといっても確率分布は1/2であり、必ず出るわけではありません。このように事象とその確率分布は分けて考えます。これもおかしな点のひとつです。状態'11'で初めてE2が起きます。
$$ \mathbf{P}'(t)= \begin{bmatrix} P_{00}'(t) \\ P_{1}'(t) \\ P_{11}'(t) \end{bmatrix}\\ \mathbf{P}(t)= \begin{bmatrix} P_{00}(t) \\ P_{1}(t) \\ P_{11}(t) \end{bmatrix} $$ として、遷移行列$\mathbf{A}$は、 $$ \mathbf{A}= \begin{bmatrix} 1-(1-c\%)\lambda_{RA} & \color{red}{(1-c\%)\lambda_{RA}} & 0\\ \color{blue}{-(1-c\%)\lambda_{RA}} & 1-\lambda_{SB} & \lambda_{SB} \\ 0 & \lambda_{SB} & 1 \end{bmatrix}\\ $$ だと言っています。赤字の遷移確率に着目してください。 $$ \mathbf{P}'(t)=\mathbf{A}\mathbf{P}(t) $$ この行列を計算すれば、 $$ \begin{eqnarray} P_{00}'(t) &=& 1-(1-c\%)\lambda_{RA}P_{00}(t) &+& \color{red}{(1-c\%)\lambda_{RA} P_{1}(t)} && \\ P_{1}'(t) &=& \color{blue}{-(1-c\%)\lambda_{RA}P_{00}(t)} &+&(1-\lambda_{SB})P_{1}(t) &+& \lambda_{SB}P_{11}(t) \\ P_{11}'(t) &=& &+&\lambda_{SB}P_{1}(t) &+&P_{11}(t) \end{eqnarray} $$ となります。符号が反対なのも変ですがそれは無視するとして、状態00から状態1へは$\color{blue}{(1-c\%)\lambda_{RA}}$だけ移るので、状態1から状態00へは、反対の符号分$\color{red}{-(1-c\%)\lambda_{RA}}$だけ移しているようです。
しかしながら、前記事でも参照した米国ロチェスター大学の資料によれば、遷移行列の要素は条件付き確率であり、マルコフ遷移図210.2によれば、状態1から状態00へは遷移しないので$\dagger$、遷移の無い条件付き確率はゼロになるため、これは重大な誤りです。
さらに、E2の確率を求めるのに、全体の確率を足していますが、全ての確率を加えると常に1になるはずで、これも誤りです。実際に参照論文中に、初期値は$\mathbf{P}(0)=[1, 0, 0]^T$とあり、AのRFにより'00'から減った分だけ'1'が増え、BのSPFにより'1'が減った分だけ'11'が増えることを思えば、総和は一定だとすぐに気づくはずです。
$$
R_{E2}(t)=P_{00}(t)+P_1(t)+P_{11}(t)\tag{参照論文の式}
$$
上記のとおり「状態'11'で初めてE2が起きる」ことから、$P_{11}(t)$のみであり、かつ故障確率であることからこの確率は信頼度ではなく不信頼度となります。従って1から引いて、
$$
R_{E2}(t)=1-P_{11}(t)=P_{00}(t)+P_1(t)\tag{正しい式}
$$
参照論文のうちの短い記述の中で6個も問題が見つかりました。これ以外に既に述べたAとBが同時に故障することは(a.s.)無いは確率論の基礎であり、重大な誤りと言えます。
https://en.wikipedia.org/wiki/Probability_density_function#Example
$\dagger$修理を考えれば遷移しますが、それは別の問題です。修理を考えていないという問題もありますね。

Leave a Comment