|
14 |
ISO 26262のFTAに関する論文 (4) |
書き換えたFTの評価
図202.1に対して図203.1の書き換えを適用したものが図204.1のFTです。このFTに対してカットセット分析を実施し、TOP事象の確率を求めます。
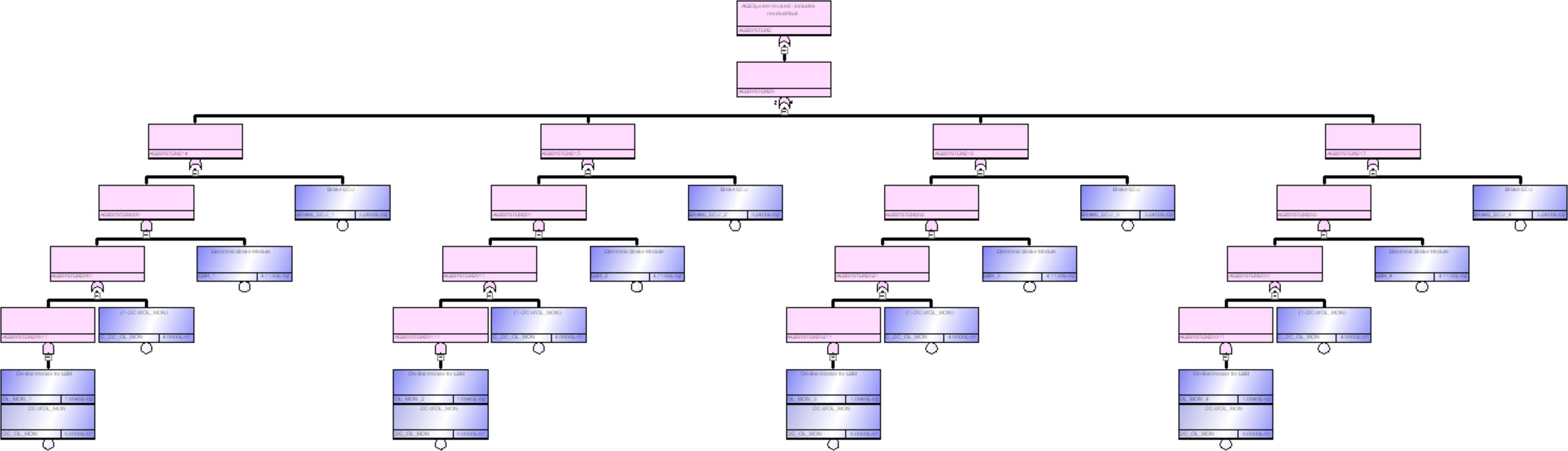
同様にツールを用いてMCSを求めると、MC数は42個に増加します。しかし前述のように、これには3個以上のエレメント故障が含まれるためツールで削除します。すると、表204.1のように24個のMCが得られ、TOP事象の確率は$4.35\times 10^{-5}$、PMHFは8.70[FIT]となります。表204.1中のC_DC_OL_MONは、1からオンラインモニタのDCを引いた定数であるため、これはエレメント故障数にカウントされません(青字で定数を表示)
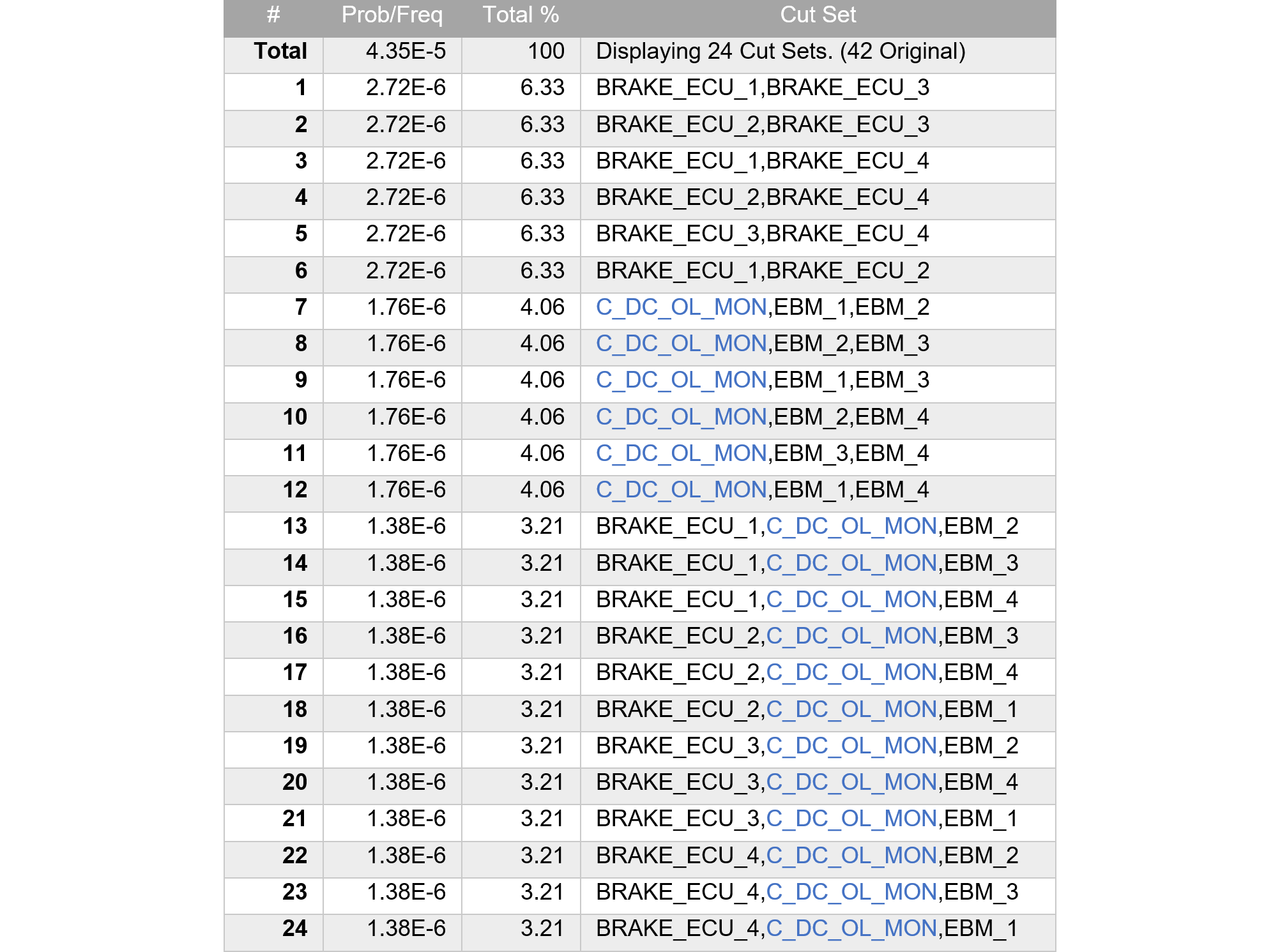
このように、PMHF式を尊重せず、LFを見逃しDPFのみとすることで、2.7倍も故障確率を甘く(低く)見る事になります。保守的に(高く)見積もるのであれば安全側なのでOKですが、不稼働確率の過小評価は危険側のため、良くありません。
再度整理すると、正しい考え方は、
- E1及びE2の2つのエレメントにより構成される冗長系は、マルコフ連鎖で表される。
- E1、E2それぞれのエレメントは修理可能(つまり不信頼度$F(t)$ではなく、不稼働度$Q(t)$となる)
- PMHF式はこれらを考慮し、系の車両寿命における平均不稼働確率Q(T)を表したものであり、 PMHF式に基づきFault Treeを構成する
ですが、参照論文はこのうち、2., 3.が満足されていません。1.は当然なので、ほとんどが間違いということになります。
RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。

Leave a Comment