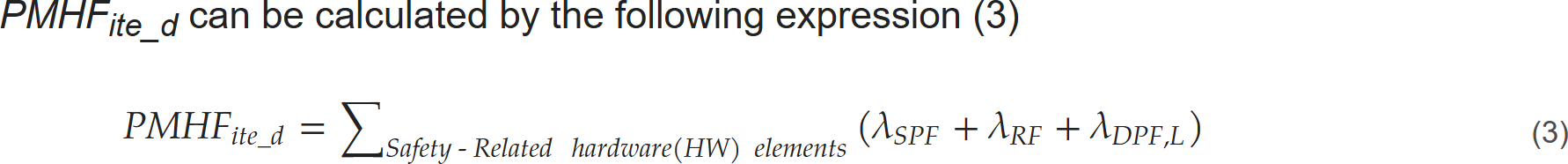PMHF式が誤っている論文は大変に多く、その元凶は2014年のこの論文$\dagger$のようですが、また発見しました。
K, Lu and Y. Chen, "Safety-Oriented System Hardware Architecture Exploration in Compliance with ISO 26262,", Appl. Sci. 12(11), MDPI, 2022.
アブストラクトの翻訳文を示します。
要約:安全性が重要な自動車用インテリジェントシステムは、動作中に厳しい信頼性が要求されます。そのため、このような安全性が重要なシステムの開発では、安全性と信頼性の問題に対処しなければなりません。しかし、安全/信頼性の要件をシステムに組み込むと、設計の複雑さが大幅に増します。さらに、国際的な安全規格はガイドラインしか提供しておらず、具体的な設計手法やフローは示されていません。そのため、システム設計および検証の複雑さに対処し、国際的な安全規格の要件も満たす、システムエンジニアを支援する効果的な安全プロセスを開発することが、重要かつ価値のある研究課題となっています。本研究では、フォールトツリーに基づく脆弱性分析と安全志向のシステムハードウェアアーキテクチャの探索を統合した、安全志向のシステムハードウェアアーキテクチャ探索フレームワークを提案します。このフレームワークにより、ISO-26262 の安全要件およびハードウェアのオーバーヘッドの制約に準拠した、効率的なソリューションを迅速に発見することができます。探索フレームワークの実行後に、故障モード、影響、および診断分析(FMEDA)レポートが生成されます。提案したフレームワークは、システムエンジニアが、コスト効率の高い方法でシステムの安全性/堅牢性の設計、評価、および強化を行うことを容易にします。
ちなみに弊社の論文も[7]及び[10]の2件が参照されているものの、数式は全く考慮されていません。
 図975.1 論文の参照文献[7]
図975.1 論文の参照文献[7]
これに対する本文での引用は以下のようです。
[7] の著者は、ISO 26262 に基づいて適用範囲を拡大するため、ミッション機能の故障率、安全機構の故障率、一次安全機構および二次安全機構の診断カバレッジ、二次安全機構の診断期間などの観測可能なパラメータを用いて、非冗長および冗長サブシステムにおける PMHF の計算のための一般化された式を提示しました。
全くこのとおりなので、このPMHF公式を参考にしてもらえば良かったのですが。
 図975.2 論文の参照文献[10]
図975.2 論文の参照文献[10]
[10] の研究は、規格の重要な前提である定期的な検査と修理を考慮しながら、定量的なFTAのフレームワークを提供することを目的としています。このフレームワークは、マルコフ確率過程のモデルと、そのモデルから導式化したPMHF方程式に基づいています。
全くこのとおりなので、定期的な検査と修理を考慮したPMHF公式を参考にしてもらえば良かったのですが。
論文は批判的に読むものであって、このように自論文の飾りにするだけでは引用としての意味がありません。
$\dagger$ †
Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.
 前のブログ
次のブログ
前のブログ
次のブログ