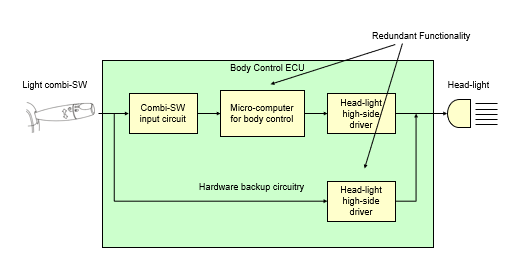
ISO 26262のコンサルティング会社が提供するPMHF式の解説動画を見つけたので見ていきます。ほとんどの論文が無視する中で、珍しくこの動画はPart 10に掲載されているPMHF式(下図738.1)をリスペクトしており、

その解説を行っています。そこまでは良かったのですが、以下の画面に誤りがあります。

英文のトランスクリプトを入手したので、画面と合わせて見てみましょう。以下はDeepLによるその翻訳です。

さて、この式を計算しようとすると、いくつかの問題にぶつかる。そこでまず我々は、1番目の欠陥に残留欠陥を加えると、この式の冒頭、1時間あたりの故障に1時間あたりの故障を加えたものになることを示したい。これは問題ない。これでいいのだ。そして、これが我々が求める実際の単位である。PMHFは1時間当たりの故障数である。

ここはちょうど画面(図777.1)上部の下記の式 $$ \frac{Failures}{hour}+\frac{Failures}{hour} $$ を意味します。これは(次元が合っているので)問題ないと言っています。ところが、

しかし、他の表現を見てみよう。1時間当たりの故障数×1時間当たりの故障数×1時間当たりの故障数×1時間当たりの故障数の2乗である。これは数学的に意味をなさない。これは規格ではあまり扱われていない。

画面下部の下記の式に移り、 $$ \frac{Failures}{hour}\times\frac{Failures}{hour}\times hour=\frac{Failures^2}{hour}\ ?? $$ このMPFの式とSPFの式の次元が合わないという主張です。これは解説動画の誤りであり、故障率の次元は動画で言う $$ \frac{Failures}{hour} $$ ではなく、 $$ \frac{1}{hour} $$ というだけのことです。従って規格にはなんら問題はありません。

故障数は1個、2個と数える無次元数です。従ってPMHFを構成するSPFもMPFも単位は故障率の次元と同じく$h^{-1}$となり加算することができます。この後の解説でFTAでは故障率の単位を$h^{-1}$と自ら言っているので、不整合に気付いても良さそうなのですが。PMHFが故障率の次元と同じであることを理解していないのかもしれません。

このように、専門家といえども誤りはあるので、「主語で語らない」$\dagger$ようにしましょう。

$\dagger$「主語で語る」というのは、「誰々さんが言ったから」「〇〇教授が言ったから」等と、無批判に主語の権威付けを利用して自説を正当化する行為

前のブログ 次のブログ

結論

最後に本論文$\dagger$の結論部分では、

安全機構とミッションブロックが異なる場合、冗長アーキテクチャMooNは異なる非同一チャネルを持つ。この場合、MooN冗長アーキテクチャの一般化PMHF公式の開発は非常に複雑になる。しかし、異なるチャネルを持つアーキテクチャ1oo2に対して式(13)で得られた結果は、両方の公式式において同一のチャネルを仮定した場合の式(9)で得られた結果と等しい。

と述べており、非対称冗長について一般化PMHFが複雑になると言いながら、同一のチャネルを仮定しているのは理解できません。複雑であっても"m"と"sm"は非対称冗長の場合、異なる故障率を持つためです。これは前稿で指摘の(iv)項です。

同じく結論部分において、

今後の研究課題としては、本論文で開発したPMHF公式をMooN冗長アーキテクチャ向けに拡張し、多点欠陥検出間隔を持つ安全機構のテストや、非同一チャネルの考慮を含めることが考えられる。

と書いており、これらが考慮されていないことは著者自身でも課題(ないしは問題)だと思っているようです。これら2つの課題は、

• MPF検出率(DC)及び検出周期$\tau$を持つ2nd SMの効果
• 非対称冗長チャネル

であり、それぞれ前稿で指摘の(ii)(iii)及び(iv)項にあたります。著者はこの考慮を今後の研究課題としていますが、ISO 26262コンプライアンスを考えれば、本来は最初からこれらの条件を含めるべきでした。

また、本論文も例に漏れず、揃って規格のPMHF式を無視していますが、一つにはPart 10は参考情報であり、そのため読まれていないのではないでしょうか？どうも規格式について全般的にリスペクトが不足しており、まともに読んで批判しているのは弊社だけのように思います。

PFHとPMHFの比較と言うのは良い着眼であり、弊社でも過去に取り上げています。それに従えば、どちらも定義は「$\img[-1.35em]{/images/withinseminar.png}$」ですが、PFHが非修理系を対象にしているのに比べ、PMHFは定期検査修理を前提にしているため、その反映により計算式は異なってくるわけです。具体的には$\img[-1.35em]{/images/withinseminar.png}$が異なり、それらが次回RAMS 2025投稿論文のテーマです。

なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。

$\dagger$E. Rogova, C. Nowak, M. Ramold, et al., "Comparison of Analytical Formulas of PFH and PMHF Calculation for M-out-of-N Redundancy Architecture," Europ. Safe. Reliab. Conf.,, pp.1-5, 2019

前のブログ 次のブログ

アブストラクトの最後

本論文$\dagger$の最初に戻ってみると、アブストラクトの最後に、

本論文で示す比較分析により、PFH公式とPMHF公式が異なるケーススタディに対して同様の結果を与えることが実証された。

と主張していますが、ISO 26262の仮定を捨ててIEC 61508と同様な非修理系という誤った仮定を導入すれば、似たような式が得られても当然です。

本来はPeriodic inspection and repair (PIR) 保守戦略に基づく不稼働度を計算すべきであり、その仮定の元ではPMHF式は似たような式にはなりません。

誤りの背景

総じてこれらの仮定の誤りはISO 26262を良く分析していないことからくるものと思われ、これはIEC 61508出身の研究者にしばしば見られる現象です。それは、IEC 61508の観点からしかISO 26262を眺められないところに原因があります。

彼らの論文や資料には特有のパターンがあり、ISO 26262の論文や資料であるにも関わらずDU, DDで始まったら要注意です。そもそもISO 26262にはDU, DD等の用語はなく、かつDU, DD故障率はオブザーバブルではないため、以下のように1st SMのカバレージであるKパラメータ$K_\text{RF}$を用いて示すべきです。 $$ \lambda_\text{DD}=K_\text{RF}\lambda_\text{IF},\ \lambda_\text{DU}=(1-K_\text{RF})\lambda_\text{IF} $$

さらに、ISO 26262に存在する故障の区別、具体的にはSPFとDPFの区別がIEC 61508には存在しません。DPFは1oo2として取り扱うべきです。多くの著者はIEC 61508には存在しないLF(以下の式の$\lambda_\text{MPF,l}$)の概念が理解できずに故障率を以下の誤りの式の如く、全て加算してしまいがちです。過去記事中の論文や資料にも同様な誤りが見られます。 $$ \lambda_\text{DD}=\lambda_\text{SPF}+\lambda_\text{RF}+\lambda_\text{MPF,l} $$

さらに、修理の概念が無いようで、ISO 26262の基本の仮定であるPIRを考慮していません。

「ISO 26262などはIEC 61508の派生ないし亜流だ」と言う誤った考えを持たないことが、ISO 26262の理解の秘訣となります。

$\dagger$E. Rogova, C. Nowak, M. Ramold, et al., "Comparison of Analytical Formulas of PFH and PMHF Calculation for M-out-of-N Redundancy Architecture," Europ. Safe. Reliab. Conf.,, pp.1-5, 2019

前のブログ 次のブログ

仮定のまとめ

本論文$\dagger$はその中程に、置いた4つの仮定をまとめてリストしています。

(i) すべての危険故障の故障率は，λD である（IEC 61508 の概念では DD と DU を区別せず，ISO 26262 の概念では SPF，RF，DPF 及び MPF を区別しない）
(ii) PFH 公式におけるプルーフテスト間隔$\tau$は、PMHF 公式における運転寿命間隔 $T_{Lifetime}$と等価である
(iii) システムは修理不可能である
(iv) チャネルが同一で独立している

これはいずれも誤りです。一項目ずつ見ていきます。

• IEC 61508はいざ知らず、ISO 26262においてはSPF, RFとは区別せず、DPF, MPFも区別せずで良いですが、それら2グループには明確な区別があります。言うまでもなく故障によるVSG確率が全く異なるため、それを考慮しなければなりません。具体的にはDPFは2重故障を意味するため、故障確率の2乗項が出現します。
• 「PMHF式では$\tau=T_{lifetime}$として良い」と言っていますが、前稿で指摘したようにこれは誤りで、ISO 26262にもプルーフテストというか定期検査修理は存在するため、テスト周期は$\tau$となり、車両寿命ではありません。反対にこう仮定すると、2nd SMの存在が無いことになります。規格書では2nd SMの存在がブロック図に書かれているにも関わらず、それが無視されています。
• ISO 26262で対象とするサブシステムは修理可能です。Part 10のPMHF式の箇所に、ドライバーがMPFを通知され、修理工場へ持ち込む表現があります。もちろんMPFを検出するのが2nd SMです。
• チャネルは前項のように、独立であっても同一ではありません。「冗長」は必ずしも対称冗長を意味しません。

以上から、論文途中の仮定リストの全点が誤っている(=ISO 26262非互換である)ため、ここから先の検討は不要となります。

$\dagger$E. Rogova, C. Nowak, M. Ramold, et al., "Comparison of Analytical Formulas of PFH and PMHF Calculation for M-out-of-N Redundancy Architecture," Europ. Safe. Reliab. Conf.,, pp.1-5, 2019

前のブログ 次のブログ

不当な仮定1

正しく引用されたことは良かったのですが、本論文$\dagger$では弊社の式に対して新たに以下の(12)という仮定を加えており、残念なことにこれでは一般性を失う不要な仮定です。

$$ \lambda_{m,MPF}=\lambda_{sm,MPF}=\lambda_{MPF}=\lambda_{D}\tag{12} $$

この(12)の意味するところは"m"も"sm"も同じ故障率を持つこと、すなわち対称冗長を意味しており、これは特殊な場合に限られます。

反例を示すと、例えば過去記事の図70.1に示すヘッドライト装置の実例のように、

メカスイッチからのON信号をメインのチャネルではマイコンで点灯し、バックアップチャネルではトランジスタで点灯するような非対称冗長には(12)は当てはまりません。以下のように"m"系の故障率のほうが"sm"系よりも巨大になるためです。 $$ \lambda_{m,MPF}\gg\lambda_{sm,MPF} $$ さらに言えば、このような非対称冗長は、特にASIL分解においては、規格ではむしろ推奨されています。マイコンに低いASILを割り当てておき、複雑なシステムの開発を容易にできる一方、壊れにくい単純なトランジスタで元の安全要求を保証できるためです。

不当な仮定2

さらに別の仮定の問題があります。弊社の式における2nd SMの検査周期である$\tau$について、$\tau=T_{lifetime}$と仮定してしまったことです。これは2nd SMが存在しないか、あるいはDCがゼロであることを意味します。これは誤った仮定です。

なぜそうしたかはその箇所には書かれていませんが、アンリペアラブルという仮定を置いているのが後からわかります。

$\dagger$E. Rogova, C. Nowak, M. Ramold, et al., "Comparison of Analytical Formulas of PFH and PMHF Calculation for M-out-of-N Redundancy Architecture," Europ. Safe. Reliab. Conf.,, pp.1-5, 2019

前のブログ 次のブログ

M-out-of-N冗長アーキテクチャにおいて、PFHとPMHFを比較するという大変興味深い論文$\dagger$をたまたま見つけたので読んでいきます。弊社の論文が引用されていたにも関わらず最近まで知りませんでした。

アブストラクト

例によって、DeepLで翻訳しながら見ていきます。まずアブストラクトから。

道路運送車両の国際機能安全規格ISO 26262は、ランダムなハードウェア故障が安全目標に違反する確率を定量的に推定する方法として、ランダムなハードウェア故障に対する確率的指標（PMHF）を用いることを提案している。PMHFの計算例はISO 26262に示されている。しかし、この規格にはM-out-of-Nの冗長アーキテクチャに対するPMHFの計算公式は含まれていない。 この公式は、冗長性の問題と冗長アーキテクチャの確率論的メトリクスの計算が特に関連するドライブ・バイ・ワイヤ・システムにおいて重要な応用を見出すことができる。

本論文では、M-out-of-N冗長アーキテクチャのPMHF計算公式を開発し、国際機能安全規格IEC 61508で定義されている高需要モードと連続需要モードの安全システムの平均危険故障頻度(PFH)公式と比較した。本論文で示す比較分析により、PFH公式とPMHF公式が異なるケーススタディに対して同様の結果を与えることが実証された。これらのケーススタディは、IEC 61508とISO 26262で定義されているさまざまなタイプの故障を考慮して調査されている。

アブストラクトに示すように、IEC 61508で定義されているPFDとPFHと、ISO 26262で定義されているPMHFを比較し、さらにMooN冗長サブシステムへの式の拡張を行ったものです。

弊社論文

弊社でも2018年以前にISO 26262のPMHFを実際のプロジェクトに適用した経験があり、さらにそのサブシステムが冗長構成であったので、PMHFの適用には悩みました。というのは2011年に発行された規格初版において、規格PMHF式は冗長に対応していなかったためです。そこで、弊社は2017年に冗長構成に対応したPMHF式の拡張を提案する論文を発表しましたが、本論文にはきちんと弊社論文が引用されています。

異なるチャネルを持つ2チャネル冗長アーキテクチャのPMHF公式は桜井によって得られている（桜井, 2018）。非同一チャネルを持つMooN冗長アーキテクチャのための一般化されたPMHF公式は非常に複雑になる。式(13)は非同一チャネルを持つ2チャネル冗長アーキテクチャのPMHF公式を示す。桜井は、一次安全機構（冗長ミッション機能を果たす）に加えて、二次安全機構（潜在的欠陥の防止）も考慮している（桜井, 2018）。本節では、桜井が開発した公式を、"M "と "SM "の二次安全機構を持たないことを念頭に、図2bに示したケーススタディに適用する：
$$ PMHF^{1oo2}=\frac{1}{2}\lambda_{m,MPF}\lambda_{sm,MPF}T_{lifetime}+\frac{1}{2}\lambda_{m,MPF}\lambda_{sm,MPF}T_{lifetime}\tag{13} $$ 式(12)で示されるように、同一チャネルの故障率は等しいことを考慮すると、式(13)は、同一チャネルを持つ1oo2アーキテクチャのPMHFの値を示す式(14)に変換できる： $$ PMHF^{1oo2}=\lambda_D^2T_{lifetime}\tag{14} $$

$\dagger$E. Rogova, C. Nowak, M. Ramold, et al., "Comparison of Analytical Formulas of PFH and PMHF Calculation for M-out-of-N Redundancy Architecture," Europ. Safe. Reliab. Conf.,, pp.1-5, 2019

前のブログ 次のブログ

Youtubeで「ISO 26262 Hardware Safety Metrics Youtube」と検索して出てきた動画にもPMHF式の誤りがありました。

PMHF式は本来確率式をベースにしていますが、この説明においても、シングルポイント確率とマルチプルポイント確率を同列に扱って、単に故障率として加算しています。マルチプルポイント確率は桁違いに小さいので同列に扱ってはいけません。

2014年の論文「Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements」が初出らしく、これを引用した全ての資料が誤りの連鎖を起こしています。以下の図326.1は過去記事の図です。

これは動画(図771.1)と同じ式ですが、既に記事#324, #325, #326, #523で指摘しているとおり誤りです。

動画(図771.1)の右下の計算もおかしく、$\lambda_\text{SPF/RF}$よりも$\lambda_\text{MPF,latent}$のほうが大きくなっていますが、実際にはこのようなことは起こりえません。一般には前者が支配的となります。論文を確認したところ、図771.2に示すように論文の表7そのままでした。

規格Part 10にPMHF式が掲載されているにも関わらず、ほとんどの論文やこのような教育資料でその式が無視され、どこかの論文の式が孫引きされているのは不思議なことです。

前のブログ 次のブログ

弊社コンテンツの3月の検索結果です。

前のブログ 次のブログ

状態$s$や行動$a$について深堀りします。

DQN（Deep Q-Network）アプローチにおいて、状態$ s $と行動$ a $は通常、問題の性質に応じて様々な形式で表現されます。Pongゲームの文脈でこれらを具体的に考えてみましょう。

状態$s$の形式

Pongゲームにおける状態は、ゲーム画面自体または画面から抽出された特徴によって表されます。FPGA実装のために、CNNを使用して画面データから特徴を抽出すると述べました。したがって、状態$ s $はCNNを通過した後の特徴ベクトルとして表されることが多いです。

• 画面データ：元の画面データは256x256のON/OFF（1ビット）データです。これをCNNに入力します。
• 特徴ベクトル：CNNからの出力は、画面データを圧縮した特徴を含むベクトルです。このベクトルのサイズはCNNの構造に依存します。たとえば、最終的な全結合層の出力が100要素のベクトルであれば、状態$ s $は100要素のベクトルとなります。

行動$a$の形式

Pongゲームでは、行動は比較的単純です。エージェント（ここではコンピュータのパドル）が取りうる行動は、「上に移動」、「移動なし」、「下に移動」の3つです。したがって、行動$ a $はこれら3つの選択肢の中から1つを選ぶことを意味し、通常は離散的な値で表現されます。

• 行動の選択肢: 3（上に移動=0、移動なし=1、下に移動=2などのようにエンコード可能）
• 行動$ a $は、選択された行動を表すスカラー値（たとえば、0、1、2）として表現されることが多いです。

精度と表現

• 状態ベクトルの精度：CNNからの出力である特徴ベクトルの各要素は、固定小数点数または浮動小数点数で表現される可能性があります。ビット数（精度）は、FPGAのリソースと精度要件に基づいて選択されます。一般的には16ビットや32ビット固定小数点数が使用されることが多いです。
• 行動の精度：行動$ a $は離散的な選択肢を表すため、多くの場合、単純な整数値（例えば、2ビットで3つの行動を表すことができます）で十分です。

このように、DQNアプローチにおいては状態$ s $と行動$ a $の具体的な形式は問題の性質によって異なりますが、Pongゲームの場合は状態がCNNによって抽出された特徴ベクトル、行動がエージェントの選択可能な動作を表す離散値となります。

次記事に続きます。

前のブログ 次のブログ

Q値について深堀りします。

DQN（Deep Q-Network）におけるQ値は、環境の状態$ s $に対して取り得る各行動$ a $の価値を評価するものです。Pongゲームのようなシンプルな環境では、エージェント（ここではコンピューターのパドル）が取りうる行動が限られています（例えば、上に移動、移動なし、下に移動）。したがって、Q値はそれぞれの行動に対する期待報酬を表すベクトルとして表現されます。

このベクトルは、取りうる行動の数と同じ要素数を持ちます。Pongゲームのケースでは、エージェントが取り得る行動が3つあるため、Q値は3要素のベクトルになります。

Q値ベクトルのビット数

Q値のビット数は、使用する数値表現（固定小数点数表現や浮動小数点数表現）に依存します。FPGA上での実装を考慮すると、リソースを効率的に使用するためには固定小数点数表現を採用することが一般的です。固定小数点数のビット数は、必要な精度と範囲に応じて選択されます。たとえば、16ビット、32ビットなどが考えられますが、実際の選択は使用するFPGAのリソース、演算の精度要件、およびシステム全体のパフォーマンス目標に基づいて決定されます。

要素数

• 行動数: 3（上に移動、移動なし、下に移動）

ビット数（例）

• 固定小数点: 16ビットまたは32ビット
  • 例えば、16ビット固定小数点数を使用する場合、それぞれのQ値は16ビットで表現されます。この場合、Q値ベクトルは合計で48ビット（3要素 x 16ビット）になります。
  • 32ビット固定小数点数を使用する場合、Q値ベクトルは合計で96ビット（3要素 x 32ビット）になります。

まとめ

PongゲームにおけるQ値は、エージェントが取りうる3つの行動に対する期待報酬を表す3要素のベクトルです。ビット数は、FPGAのリソース、演算の精度要件、およびパフォーマンス目標に応じて選択される固定小数点表現に依存します。リソースを効率的に使用しつつ、適切な精度を確保するために、ビット数を慎重に選定する必要があります。

前のブログ 次のブログ