PMHFの算出法について以下の動画を見つけました。どうやらコンサル会社のビデオのようです。https://youtu.be/ndG1Kcc89hs

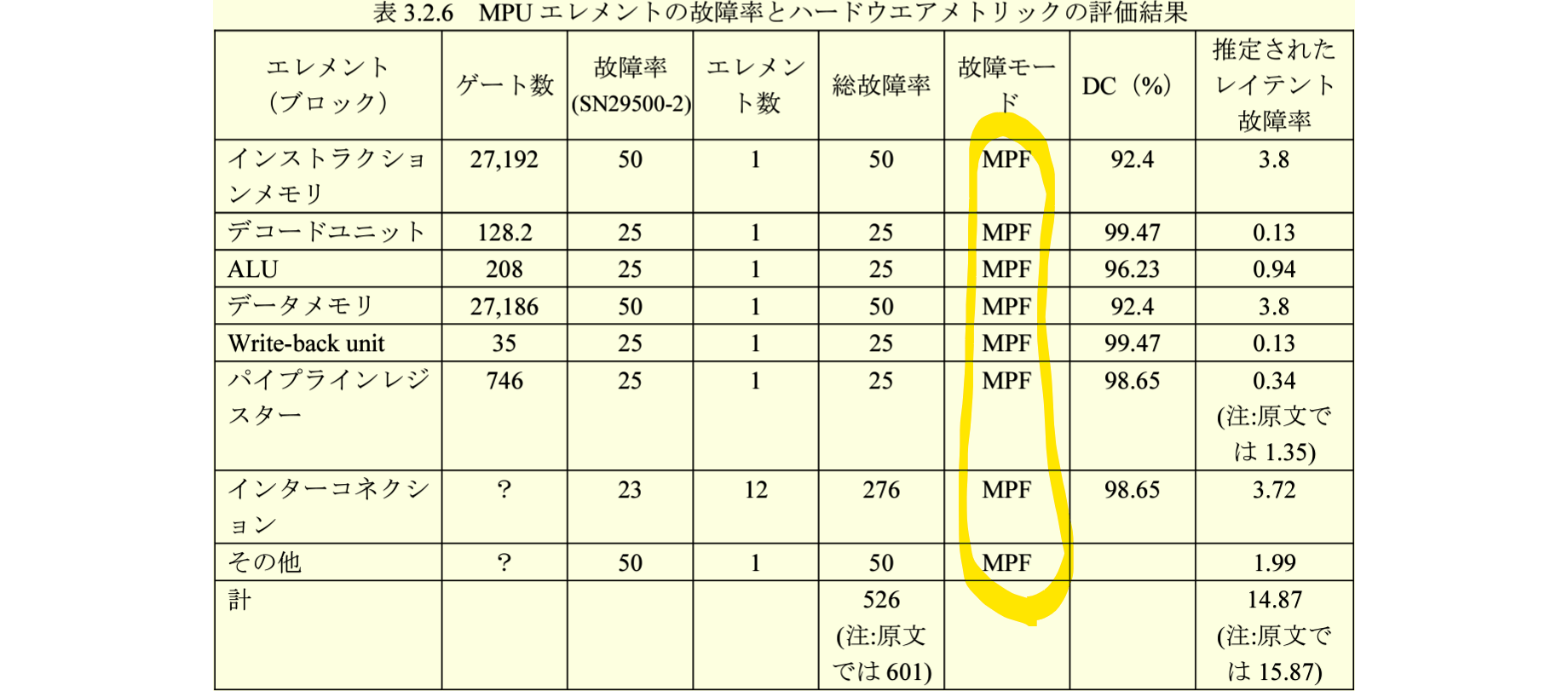
メディニアナライザを使用したようですが、PMHFの値は一見して誤っています。

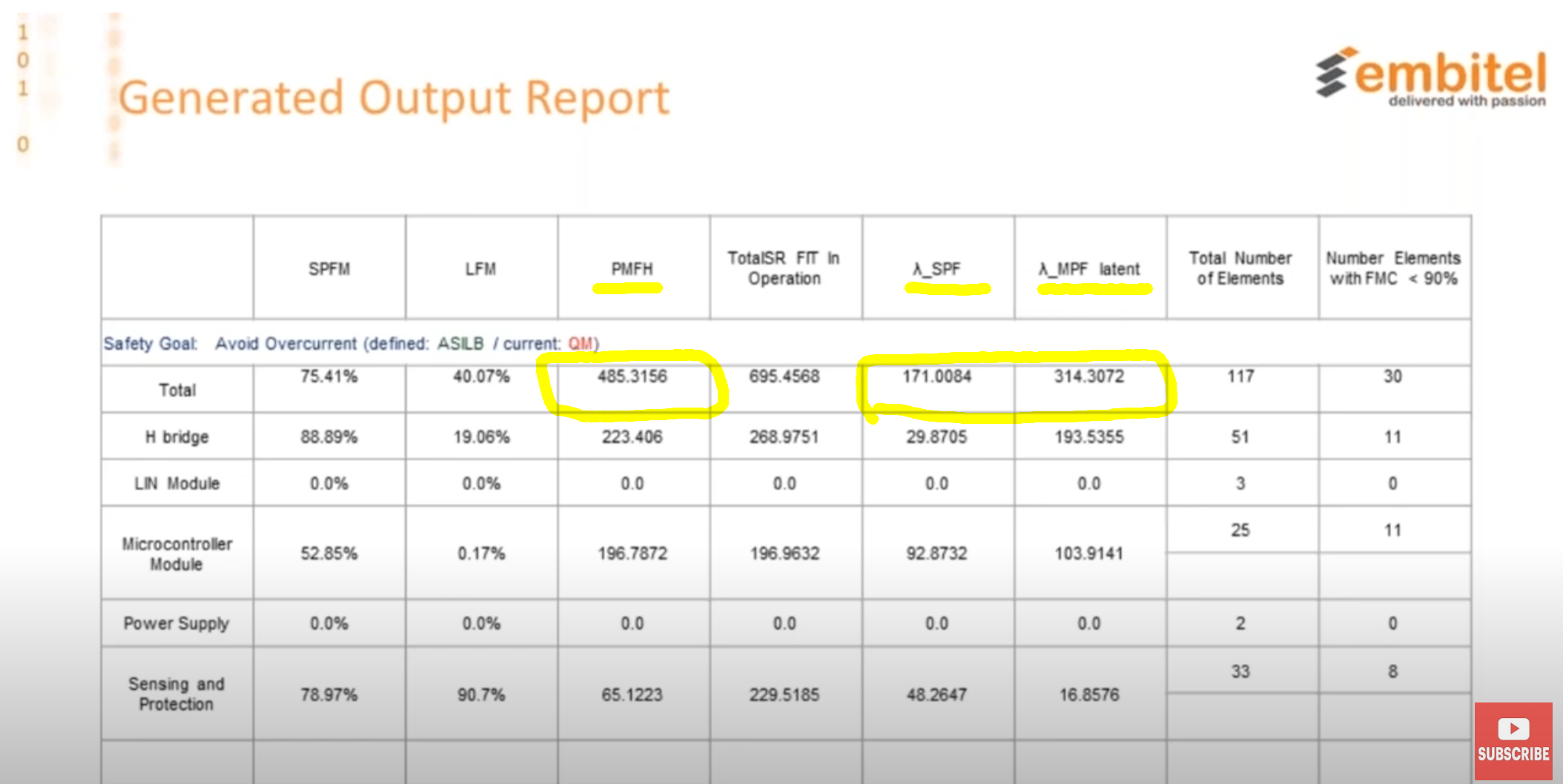
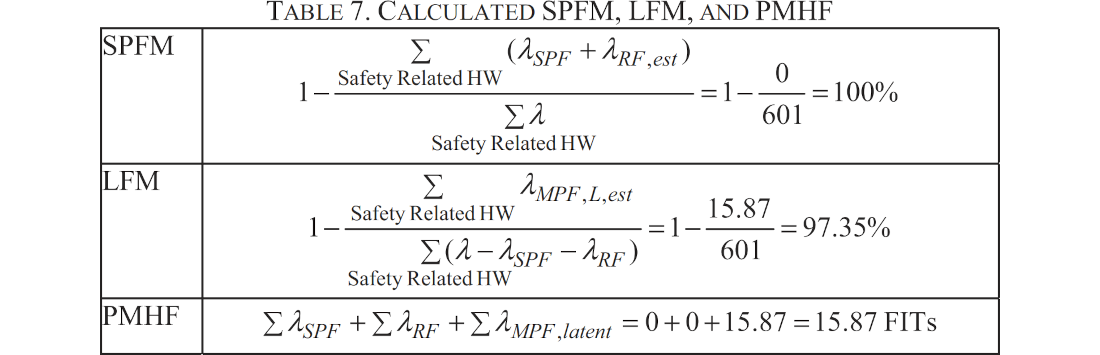
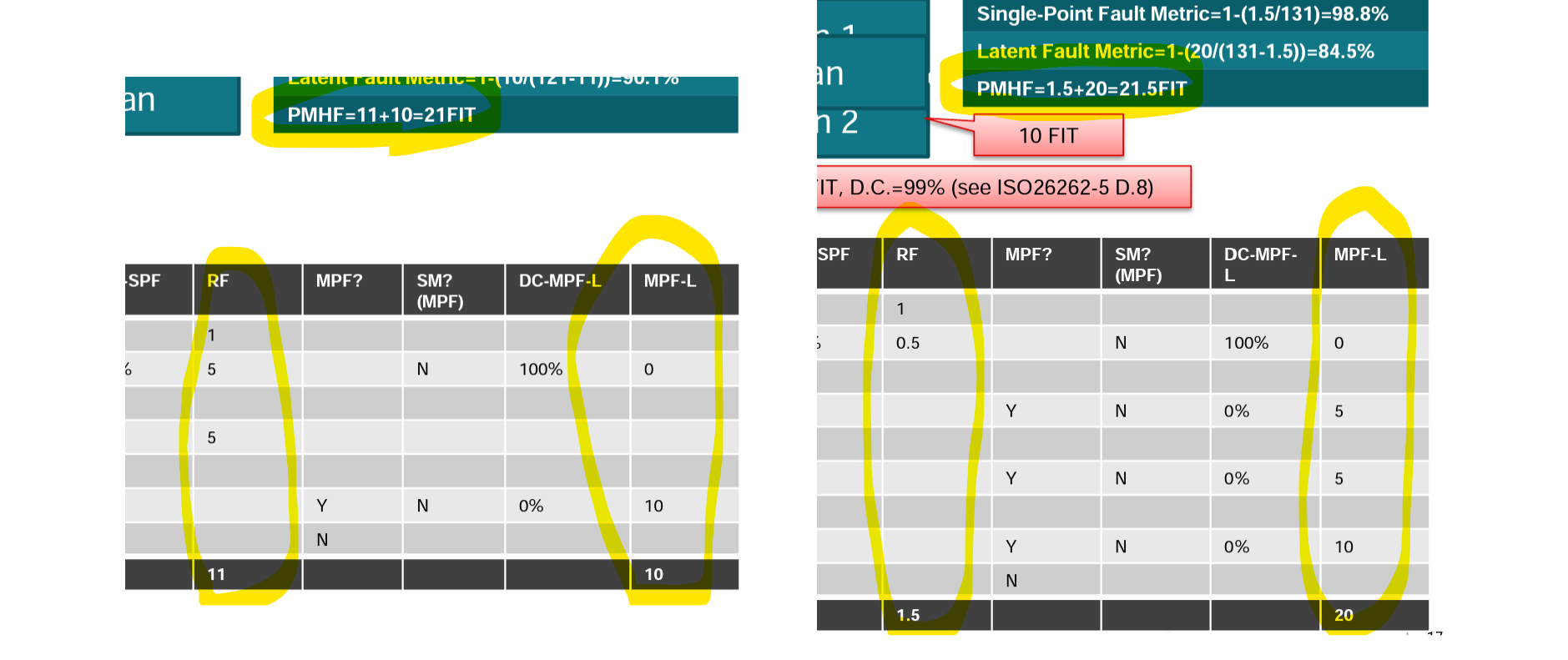
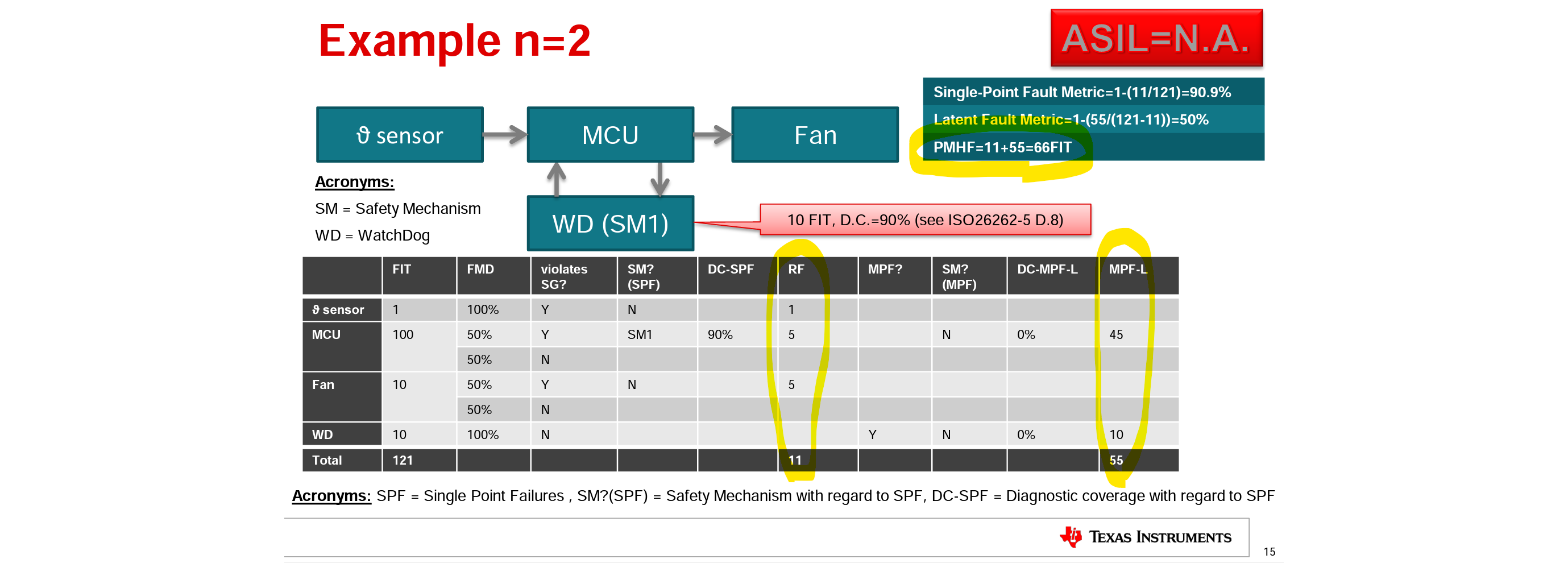
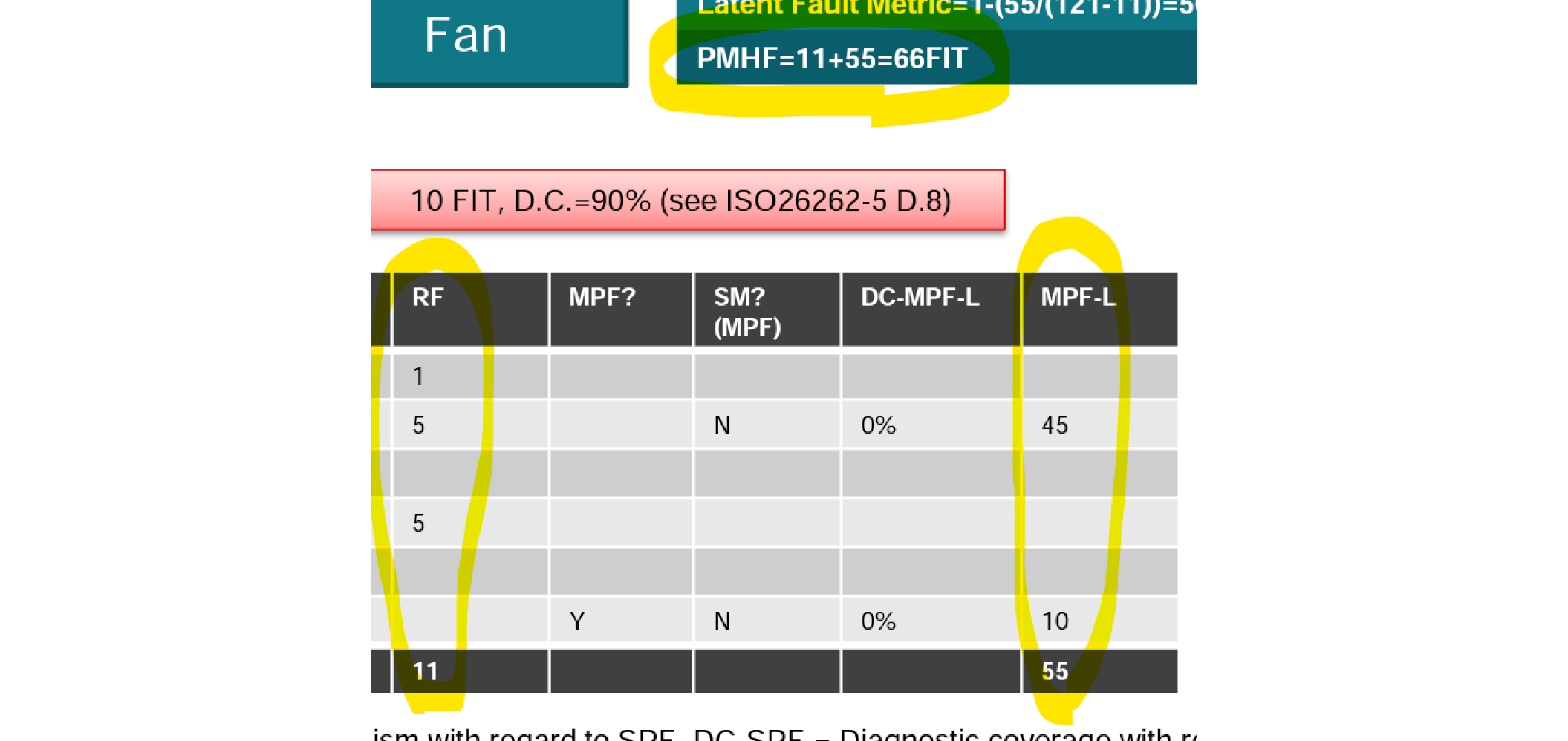
表の数値を見る限り、計算方法はSPFとDPFを加えて $$ PMHF=\lambda_\text{SPF}+\lambda_\text{MPF, latent} $$ となっているようです。

この誤りは大変多く、過去にも

• https://fs-micro.com/post/show/id/324.html
• https://fs-micro.com/post/show/id/325.html
• https://fs-micro.com/post/show/id/326.html

と複数あり、それらの誤りは以下の論文$\dagger$が元凶のようです。

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

一方、以下に前記事にもあるようにPart 5のAnnex Fに掲載されている近似式を示します。 $$ PMHF=\lambda_\text{SPF}+\lambda_\text{MPF, latent}\cdot\lambda_\text{MPF, detected}\cdot T_\text{lifetime} $$ この式はSPFとDPFを正しく意識し、それぞれを確率に直してから加え、最後に車両寿命で割っています。

それにしてもPMHFを算出する人たちはなぜ規格Part 10の、もしくはPart 5(上記)の式を用いずに、誤りの論文$\dagger$の式を参照するのでしょうか？参考にするならせめて規格式を参考にすれば良いと思うのですが。

前のブログ 次のブログ

Youtubeで「ISO 26262 Hardware Safety Metrics Youtube」と検索して出てきた動画にもPMHF式の誤りがありました。

PMHF式は本来確率式をベースにしていますが、この説明においても、シングルポイント確率とマルチプルポイント確率を同列に扱って、単に故障率として加算しています。マルチプルポイント確率は桁違いに小さいので同列に扱ってはいけません。

2014年の論文「Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements」が初出らしく、これを引用した全ての資料が誤りの連鎖を起こしています。以下の図326.1は過去記事の図です。

これは動画(図771.1)と同じ式ですが、既に記事#324, #325, #326, #523で指摘しているとおり誤りです。

動画(図771.1)の右下の計算もおかしく、$\lambda_\text{SPF/RF}$よりも$\lambda_\text{MPF,latent}$のほうが大きくなっていますが、実際にはこのようなことは起こりえません。一般には前者が支配的となります。論文を確認したところ、図771.2に示すように論文の表7そのままでした。

規格Part 10にPMHF式が掲載されているにも関わらず、ほとんどの論文やこのような教育資料でその式が無視され、どこかの論文の式が孫引きされているのは不思議なことです。

前のブログ 次のブログ

故障分類フローでの検証 (続)

前稿で規格の故障分類フローの箱(p)まで見たので、その続きを確認します。

Fraction of faults that the safety mechanism prevents from directly violating the safety goal?

安全機構が安全目標に直接違反することを防いだフォルトの割合？

とあります。ここに来たフォールトはVSGを起こします。ここから右と下の枝の違いはSMがそれを防いだかどうか(ゼロイチではなく割合)です。

VSGを防げない部分の割合を故障率$\lambda_\text{FMi,PVSG}$にかけて下の箱(r)、(s)へ移ります。これが残存フォールト$\lambda_\text{FMi,RF}$の箱(s)です。ということで、直接侵害する故障のうち、安全機構でカバーされない部分は残存フォールトだという結論です。マルチプルポイントフォールトではありません。

被引用論文の調査

ここで、「研究成果報告書」の引用元論文であるPMHF式の誤り論文$\dagger$を再度確認したところ、そこにも同じ図526.1の表が有り、全てMPFと分類されていました。そのため元論文$\dagger$から表を引き写したための誤りと判明しました。当該箇所を引用すれば、

Note that each fundamental building block in our exemplary safety microprocessor is protected with SM. This causes every hardware failure mode is classified as MPF. As the result, the summation of the single-point fault and the residual fault is zero.

各基本構成要素はSMで保護されている。 このため、すべてのハードウェア故障モードがMPFに分類される。その結果、一点故障と残留故障の和はゼロになる。

とあり、結論として元論文$\dagger$の2個目の誤りがそのまま引き継がれたようです。まとめれば、元論文$\dagger$には

1. PMHF式のDPF項を過剰に見積もる(故障率が2乗されていない)誤り
2. 故障分類において残存フォールトを全てマルチプルポイントフォールトと勘違いする誤り

の二重の誤りが存在しており、それが「研究成果報告書」をカスケード故障させたということになります。元の誤りは罪深く、その引用だけでも4～5本ほどあり、さらに今後孫引きされることを考えると、増殖する害虫を見るようで憂慮するばかりです。

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

前のブログ 次のブログ

故障分類フローでの検証

念のため残存フォールトとなるかどうか、過去記事でも解説した故障分類フローを用いて確認します。

図172.1の上方の箱(k)において、

Fraction of faults that in absence of a safety mechanism have the potential to dicrectry violated the safety goal?

安全機構が無い場合、安全目標に違反する可能性のある故障の割合は？

この表現が誤解の元かもしれませんが「安全機構が無い場合」とは、安全機構が配備されていない場合ではありません。安全機構を仮に無いものとすることを示しています。実はこの箱(k)でやりたいのは主機能か、安全機構かの見極めです。

もし安全機構の配備であれば、安全目標を直接侵害せず(no potential)、全てのエレメントが安全機構と判定されてしまうので、仮に安全機構を取り除いて考えます。そうすると、主機能であれば安全機構が配備されていても、仮に無いものと考えると安全目標を直接侵害するため、下の箱(l)に移ります。

このように、先の引用(k)の"in absence of a safety mechanism"が安全機構が無い場合と間違い易いのですが、安全機構の有無を判断するのは次のひし形の箱(m)です。

Are there safety mechanisms in place to control faults for at least one failure mode of the element (yes/no)?

エレメントの少なくとも1つの故障モードに対して、故障を制御する安全機構があるか（yes/no）？

ここでは安全機構の配備の有無を聞いています。これで分かるように、もし箱(k)が安全機構の有無であって、無い場合に下のひし形の箱(m)に来たなら、再度安全機構の有無を聞くのはおかしいはずです。

前のブログ 次のブログ

どこが誤りの起点かを調査します。まず、前稿の図527.2において、「研究成果報告書」を引用していますが、

3.1項の(15)のシングルポイント故障の定義の備考2に示されているように、安全機構が定義されている場合、シングルポイント故障にならないので、全ての故障モードはマルチプルポイントフォールトに分類される

とあります。これは誤りです。「研究成果報告書」における規格の引用箇所を確認します。

たしかに規格には「シングルポイントフォールトとならない」とありますが、とはいえマルチプルポイントフォールトには絶対になりません。その理由は最初の部分に書かれているように、安全目標を直接侵害するフォールトだからです。マルチプルポイントフォールトの定義は、別のエレメントのフォールトとの組み合わせにより安全目標侵害(VSG)となるフォールト、つまり安全目標を直接侵害しないフォールトです。

実際には図528.1備考1にもあるとおり、安全機構がある場合はシングルポイントフォールトにはならずに、残存フォールトとなります。「研究成果報告書」における規格の引用箇所を確認します。

以上まとめると、「研究成果報告書」の筆者は故障分類フローを見ておらず、シングルポイントフォールトでなければマルチプルポイントフォールトだという思い違いにより、残余フォールトが全てゼロという結果となったと考えられます。

ところがこの文章の前に故障分類フローも記述されていました。であれば、この誤りはどこから来たのでしょうか？

前のブログ 次のブログ

過去記事で財団法人日本電子部品信頼性センター発行の「平成26年度 電子部品信頼性調査研究委員会 研究成果報告書」におけるPMHF式の誤りを指摘しました。それは例のPMHF式の誤り論文$\dagger$から来ているものでした。

指摘した記事の最後に、

もっとも$\lambda_\text{SPF/RF}$がゼロならDPF項は必ず100%ですが、そもそも$\lambda_\text{SPF/RF}$がゼロという点が信じられません。その理由はDPF項は経験的に3%未満だからです。

とありますが、なぜ$\lambda_\text{SPF/RF}$がゼロになるかの原因を調べました。すると驚くべきことが分かりました。全てのフォールトがMPFに分類されているため$\lambda_\text{SPF/RF}$がゼロとなっています。この「研究成果報告書」の当該部分を図527.1に示します。

との記述がありました。通常SMが付いている回路がほとんどなので、この記述に従えば全ての回路のRFがゼロになってしまいます。これは故障分類の誤りであり、「安全機構が定義されている場合...残存フォールトは0になる」という記述では、いかなるSMでもカバレージは常に0%になってしまいます。

安全機構がある場合、一旦取り除いて考えるのが機能安全の基本です。

前のブログ 次のブログ

また、別の論文 "Safety-Oriented System Hardware Architecture Exploration in Compliance with ISO 26262"において、PMHF式の問題点を発見しました。この論文も例のPMHF式の誤り論文$\dagger$を下敷きにし、誤りを再生産しています。この誤りの連鎖はどうしたら止められるのでしょうか。

この論文の当該部分を図526.1に示します。

繰り返しになりますが、$\lambda_\text{MPF,l}$は、PMHFに単純に足すことはできません。シングルポイントとレイテントフォールトの危険度は桁違いに異なります。具体的には単一の故障率どうしで比較するのではなく、確率で比較しなければならないため、レイテントフォールトの場合はさらに別のフォールトの生起確率をかける必要があります。つまりDPF確率が問題となってきます。

従って、それらを一緒にすることはレイテントフォールト確率の過剰評価となります。実際の経験ではレイテントフォールトの効果は3%未満でした。従って理論的には無視できませんが、実際上は無視しても良いレベルの値と言えます。

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

前のブログ 次のブログ

またPMHF式の誤り論文$\dagger$(記事はここ)の誤りが他の論文に波及しているのを発見しました。 "A Novel Method to Speed-Up the Evaluation of Cyber-Physical Systems (ISO 26262)"という論文です。

この論文の当該部分を図523.1に示します。

和訳を付けると、

ランダムハードウェア故障のための確率的メトリック(PMHF): PMHFは、一点故障、残留故障、二点故障による安全目標違反の残留リスクを評価する。 違反の最大確率の定量的な目標値を定義する。 以下の式は、単一点故障、残留故障、二点故障を引き起こす各ハードウェア部品の故障モードに対する故障率を推定する(ISO 61508)。

まずISO 61508という規格は有りません。IEC 61508のtypoだとして、その中にPMHFは定義されていません。おそらくPMHF式の誤り論文$\dagger$において、

ISO 26262にはPMHF式が出ていないため(実際はPart 10に書かれている)、IEC 61508を参照する

と書かれていたので、その誤りが伝播したものと思われます。裏を取ることをしないのでしょうか。

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

前のブログ 次のブログ

TIのプレゼン資料においてPMHFの誤解の続きです。

本資料では他の例でも全て計算が誤っていました。一貫してPMHF=RF+MPF-Lとしています。

図521.1左の計算は $$ \lambda_\text{RF}+\lambda_\text{MPF,lat}=11+10=21 [FIT] $$ 図521.1右の計算は $$ \lambda_\text{RF}+\lambda_\text{MPF,lat}=1.5+20=21.5 [FIT] $$ のようにそのまま加算を行っていますが、これは誤りです。

これは前述のようにPMHF式の誤り論文$\dagger$(図326.1)から来たものと推測します。このように一か所の"欠陥"が複数に伝播し"カスケード故障"を起こしているところを見ると、システマティックフォールトに対して"安全機構"が働いていないようです。言うまでも無く"安全機構"はこの場合、自分の頭で考えることであり、論文を鵜呑みにすることではありません。

これが誤りである理由を定性的に説明します。

1. 故障率に車両寿命をかけると、車両寿命間に故障する故障確率になります。
2. 故障確率から考えると、SPF及びRFは一点の部品欠陥で車両の故障につながるため、この項はOKです。
3. ところが、MPF-Lはレイテントフォールトなので、一点のフォールトが起きても直ちに車両の故障とはなりません。つまりMPF-Lを過大に評価していることになります。
4. 本来はレイテントフォールトは別のフォールトとの組み合わせにより車両故障、つまり安全目標違反となるため、確率としてはもう一つ別の故障率が必要となります。
5. 本来はこの項は桁違いに小さくなるはずです。

過去記事でも同じことを指摘しています。

LFは単一ではVSGを引き起こさないため、アイテムのVSG確率としては、他のフォールトとのDPFとして計算しなければなりません

以上から、単一点(シングルポイント)及び残余(レシデュアル)の故障率と、レイテントフォールトの故障率を単純に加えることは誤りです。

前のブログ 次のブログ

TIのプレゼン資料においても同様のPMHFの誤解を発見しました。これも以前の記事で指摘したように、PMHF式の誤り論文$\dagger$が波及したのかもしれません。図520.1は表紙です。

資料中のPMHF計算の誤りを図520.2に示します。

図520.2の部分を拡大します。

$\dagger$Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.

前のブログ 次のブログ