*Saphire 8.2.9
TEST =
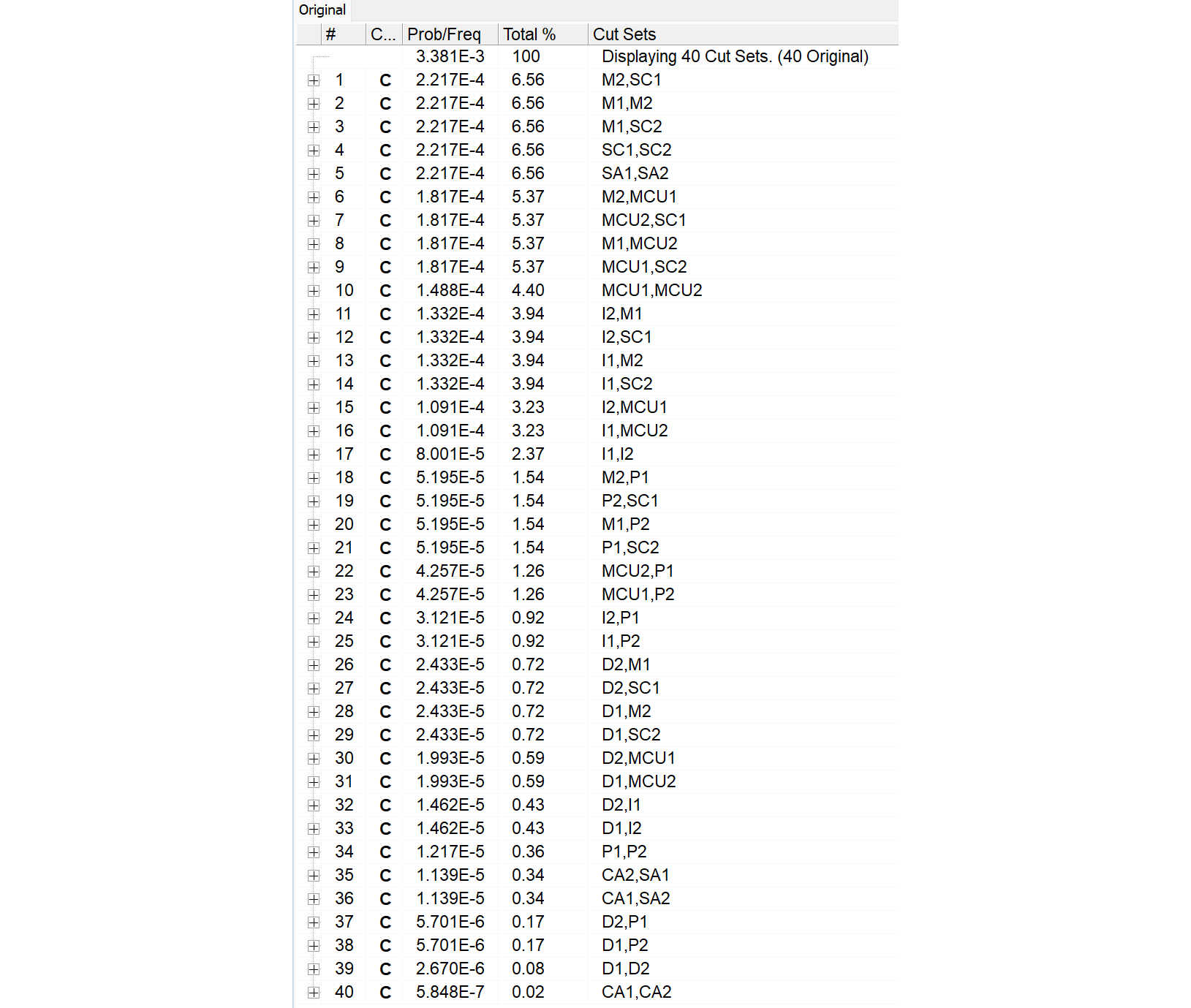
* Name ,FdT,UdC,UdT,UdValue,Prob,Lambda,Tau,Mission,Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
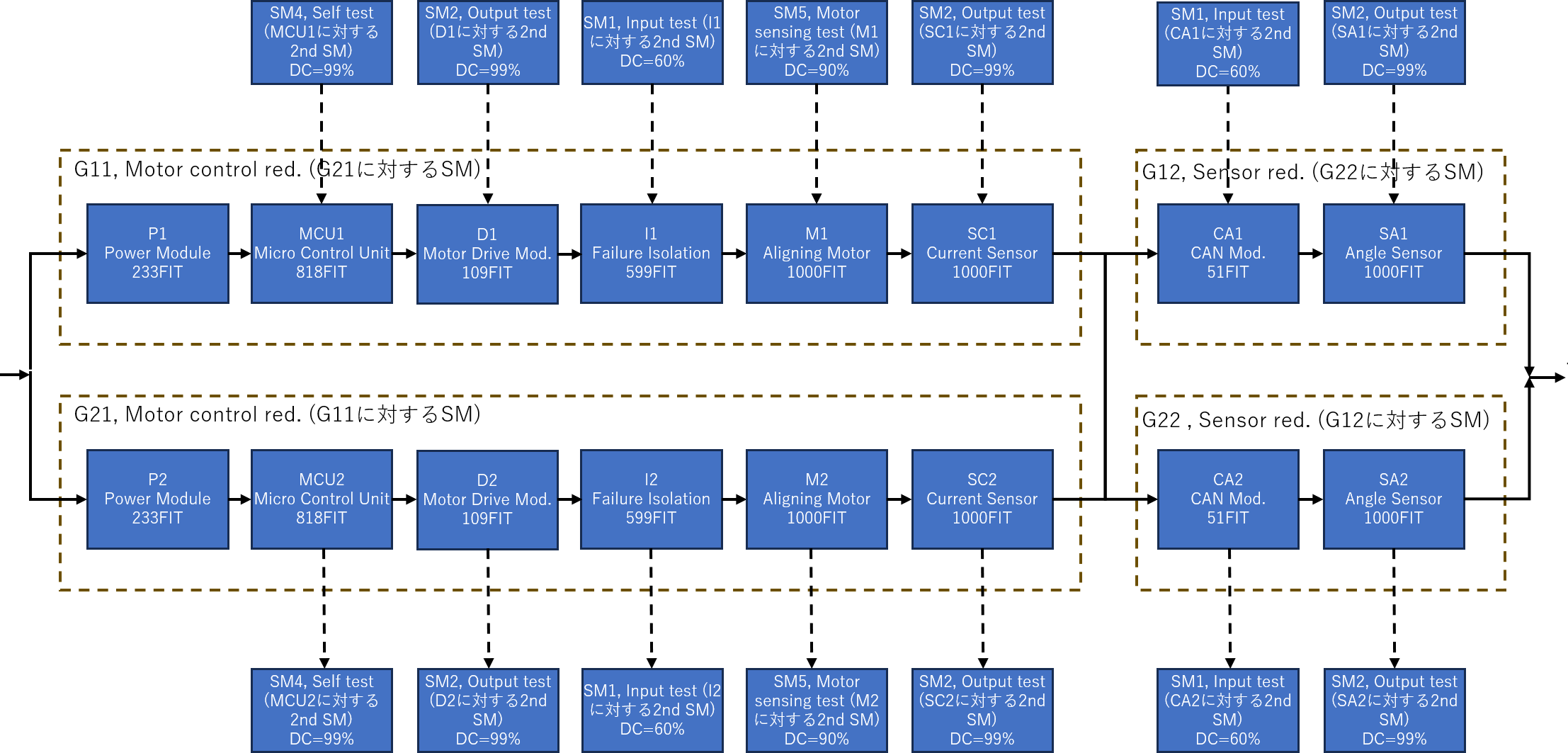
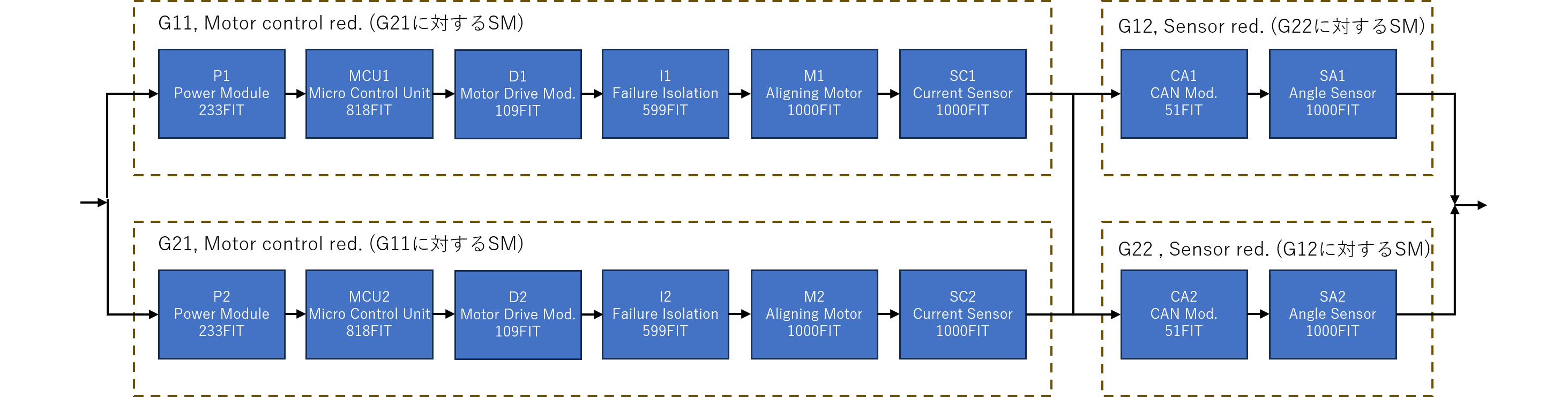
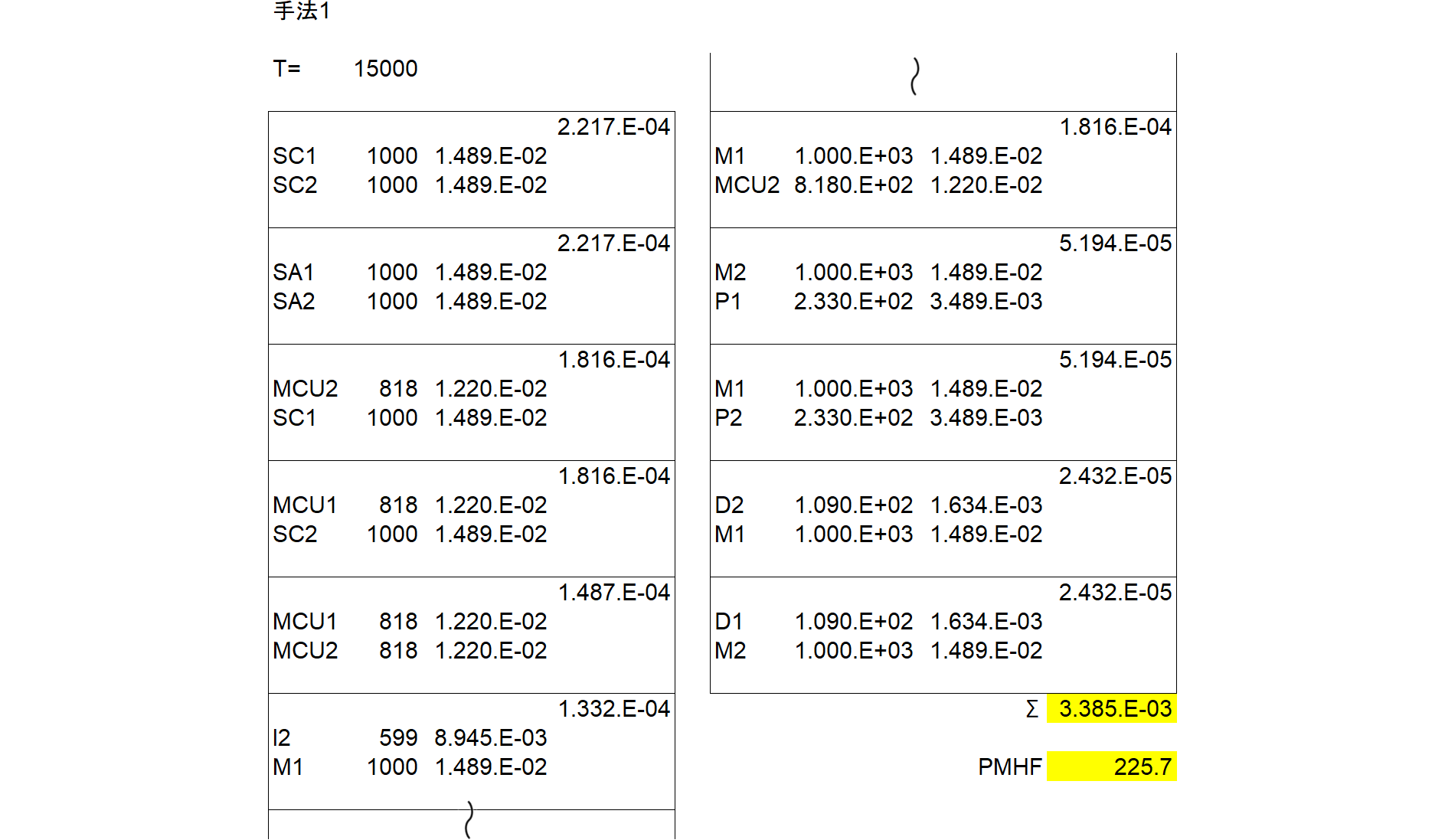
P1 ,3, , ,0.000E+000,0.000E+000,2.330E-07,0,1.500E+004, , ,0.000E+000,3.489E-03, ,RANDOM,CD,TEST
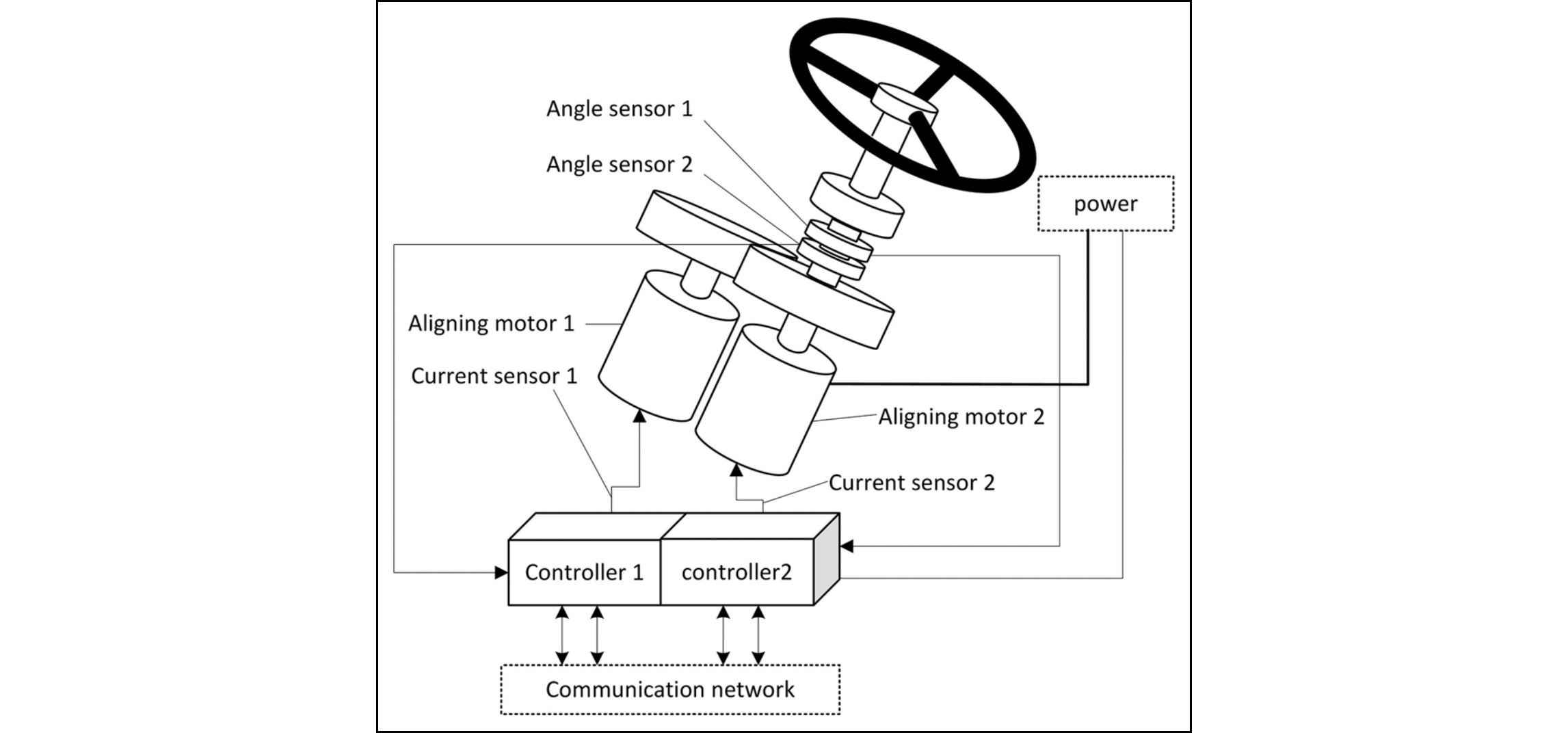
MCU1 ,3, , ,0.000E+000,0.000E+000,8.180E-07,0,1.500E+004, , ,0.000E+000,1.220E-02, ,RANDOM,CD,TEST
D1 ,3, , ,0.000E+000,0.000E+000,1.090E-07,0,1.500E+004, , ,0.000E+000,1.634E-03, ,RANDOM,CD,TEST
I1 ,3, , ,0.000E+000,0.000E+000,5.990E-07,0,1.500E+004, , ,0.000E+000,8.945E-03, ,RANDOM,CD,TEST
M1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
SC1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
CA1 ,3, , ,0.000E+000,0.000E+000,5.100E-08,0,1.500E+004, , ,0.000E+000,7.647E-04, ,RANDOM,CD,TEST
SA1 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
P2 ,3, , ,0.000E+000,0.000E+000,2.330E-07,0,1.500E+004, , ,0.000E+000,3.489E-03, ,RANDOM,CD,TEST
MCU2 ,3, , ,0.000E+000,0.000E+000,8.180E-07,0,1.500E+004, , ,0.000E+000,1.220E-02, ,RANDOM,CD,TEST
D2 ,3, , ,0.000E+000,0.000E+000,1.090E-07,0,1.500E+004, , ,0.000E+000,1.634E-03, ,RANDOM,CD,TEST
I2 ,3, , ,0.000E+000,0.000E+000,5.990E-07,0,1.500E+004, , ,0.000E+000,8.945E-03, ,RANDOM,CD,TEST
M2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
SC2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
CA2 ,3, , ,0.000E+000,0.000E+000,5.100E-08,0,1.500E+004, , ,0.000E+000,7.647E-04, ,RANDOM,CD,TEST
SA2 ,3, , ,0.000E+000,0.000E+000,1.000E-06,0,1.500E+004, , ,0.000E+000,1.489E-02, ,RANDOM,CD,TEST
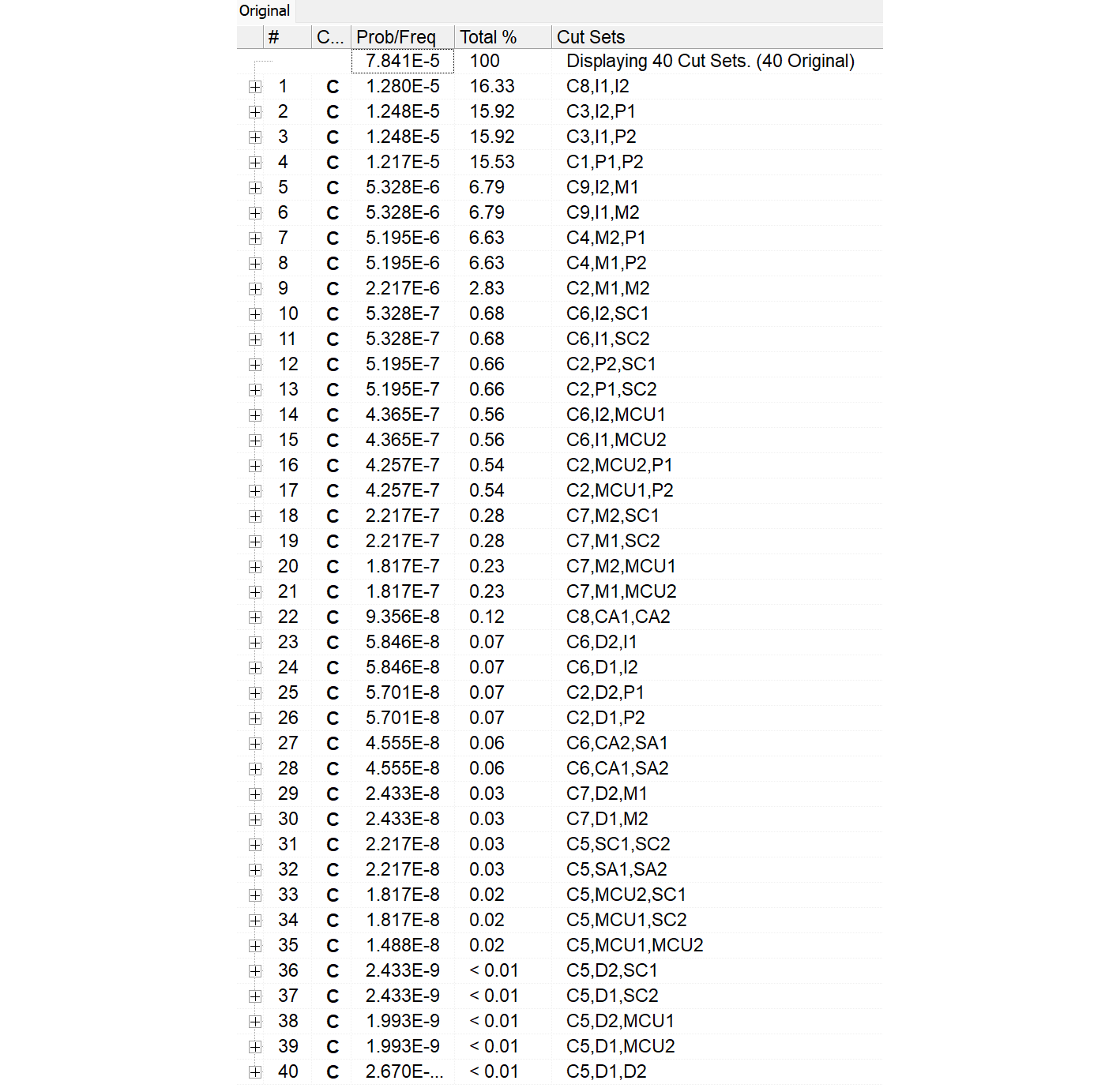
C1 ,1, , ,0.000E+000,1.0000E+00,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E+00, ,RANDOM,CD,TEST
C2 ,1, , ,0.000E+000,1.0000E-02,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-02, ,RANDOM,CD,TEST
C3 ,1, , ,0.000E+000,4.0000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-01, ,RANDOM,CD,TEST
C4 ,1, , ,0.000E+000,1.0000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-01, ,RANDOM,CD,TEST
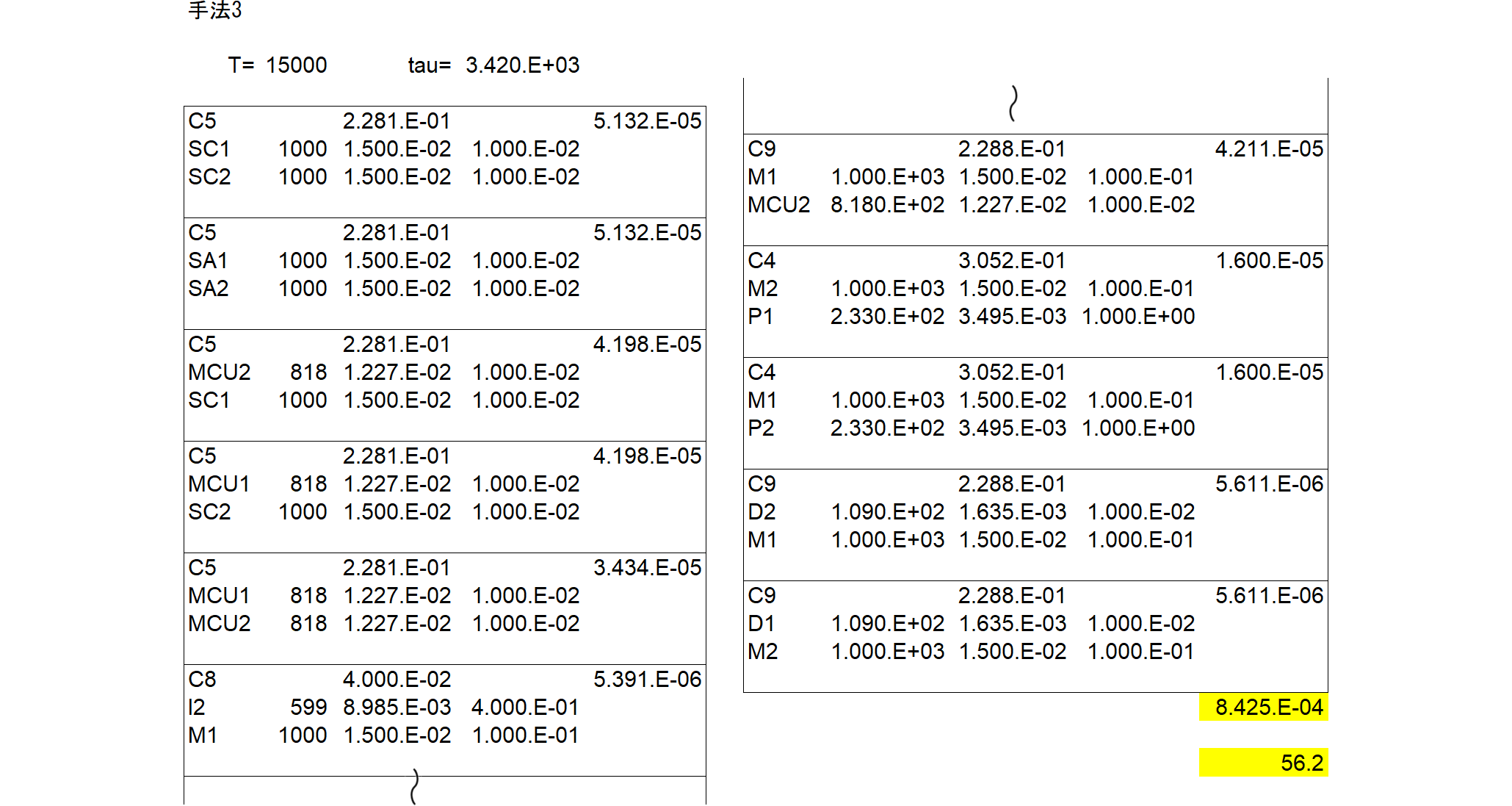
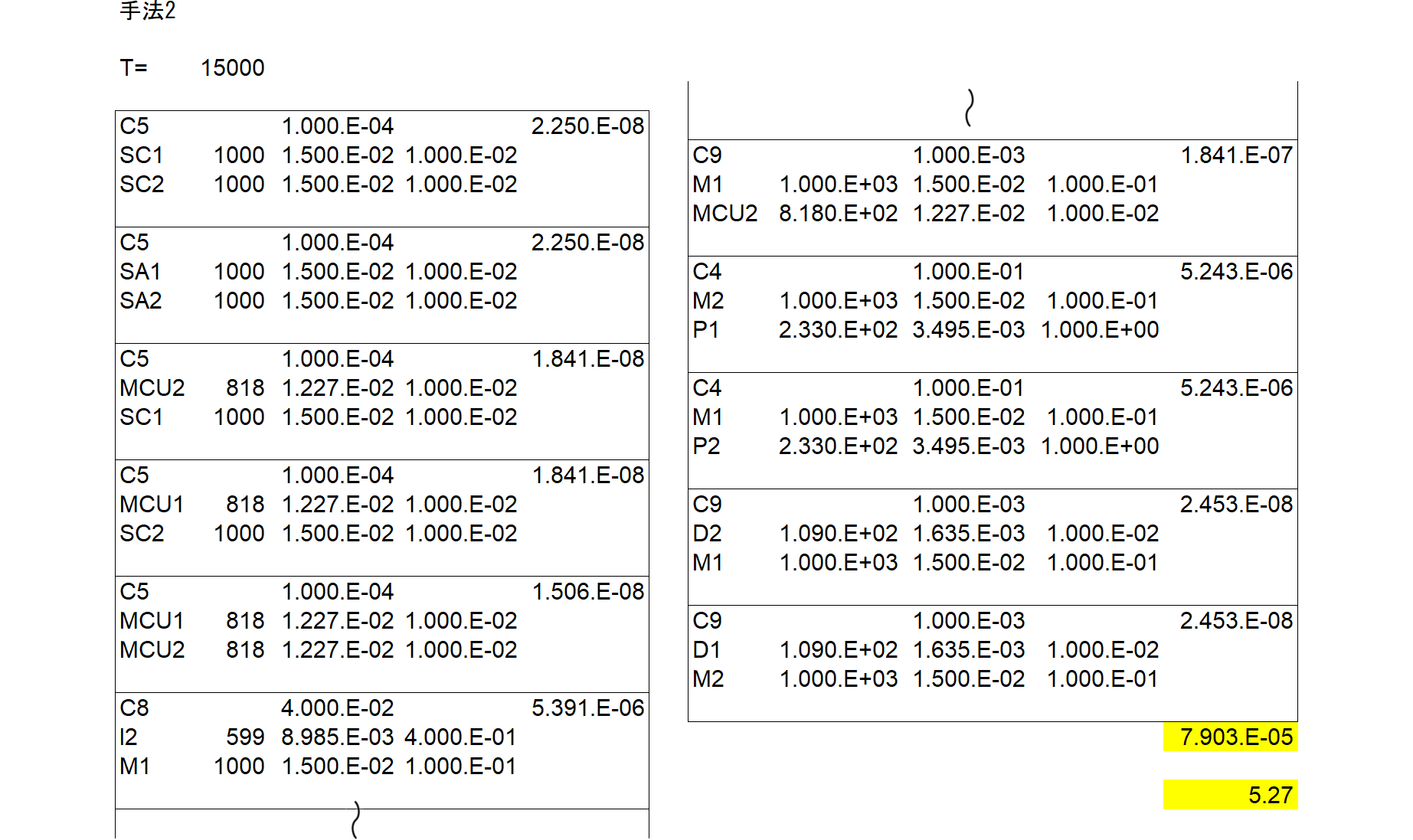
C5 ,1, , ,0.000E+000,1.0000E-04,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-04, ,RANDOM,CD,TEST
C6 ,1, , ,0.000E+000,4.0000E-03,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-03, ,RANDOM,CD,TEST
C7 ,1, , ,0.000E+000,1.0000E-03,0.000E+000,0,0.000E+000, , ,0.000E+000,1.0000E-03, ,RANDOM,CD,TEST
C8 ,1, , ,0.000E+000,1.6000E-01,0.000E+000,0,0.000E+000, , ,0.000E+000,1.6000E-01, ,RANDOM,CD,TEST
C9 ,1, , ,0.000E+000,4.0000E-02,0.000E+000,0,0.000E+000, , ,0.000E+000,4.0000E-02, ,RANDOM,CD,TEST
TEST=
* Name , Description, Project
METHOD2 ,Method2TopGate ,TEST
MCS01 ,Pair01, TEST
MCS02 ,Pair02, TEST
MCS03 ,Pair03, TEST
MCS04 ,Pair04, TEST
MCS05 ,Pair05, TEST
MCS06 ,Pair06, TEST
MCS07 ,Pair07, TEST
MCS08 ,Pair08, TEST
MCS09 ,Pair09, TEST
MCS10 ,Pair10, TEST
MCS11 ,Pair11, TEST
MCS12 ,Pair12, TEST
MCS13 ,Pair13, TEST
MCS14 ,Pair14, TEST
MCS15 ,Pair15, TEST
MCS16 ,Pair16, TEST
MCS17 ,Pair17, TEST
MCS18 ,Pair18, TEST
MCS19 ,Pair19, TEST
MCS20 ,Pair20, TEST
MCS21 ,Pair21, TEST
MCS22 ,Pair22, TEST
MCS23 ,Pair23, TEST
MCS24 ,Pair24, TEST
MCS25 ,Pair25, TEST
MCS26 ,Pair26, TEST
MCS27 ,Pair27, TEST
MCS28 ,Pair28, TEST
MCS29 ,Pair29, TEST
MCS30 ,Pair30, TEST
MCS31 ,Pair31, TEST
MCS32 ,Pair32, TEST
MCS33 ,Pair33, TEST
MCS34 ,Pair34, TEST
MCS35 ,Pair35, TEST
MCS36 ,Pair36, TEST
MCS37 ,Pair37, TEST
MCS38 ,Pair38, TEST
MCS39 ,Pair39, TEST
MCS40 ,Pair40, TEST