|
16 |
$M_\text{PMHF}$の計算 (9) |
IFRモデル
全く同様な計算をIFRモデルでも行います。同様に(2)を(2a)と(2b)に分離します(図222.1の赤矢印)。
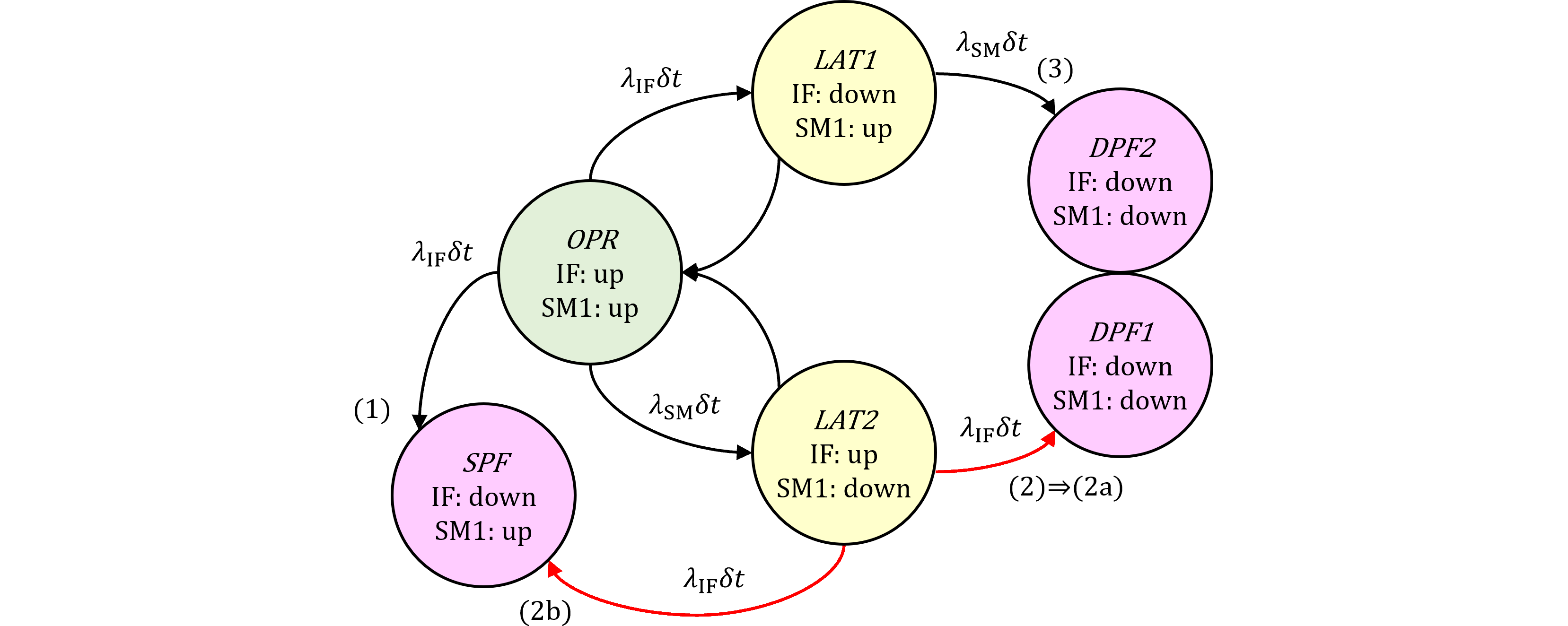
次に(2b)のSPF方向への確率積分は、IFUモデルと変わりません。SPFは、IFのフォールトがアンプリベンタブル(VSG抑止不可)な場合に起きるためです。 $$ \begin{eqnarray} \overline{q_{\mathrm{SPF(2b),IFR}}}&=&\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF(2b)\ at\ }T_\text{lifetime}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{LAT2\ at\ }t\cap\mathrm{IF^U\ down\ in\ }(t, t+dt]\\ & &\cap\overline{\mathrm{VSG\ of\ IF\ preventable}}\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ \mathrm{LAT2\ at\ }t\}\\ & &\ \ \ \ \cdot\Pr\{\mathrm{LAT2\ at\ }t\}\Pr\{\overline{\mathrm{VSG\ of\ IF\ preventable}}\} \end{eqnarray} \tag{222.6} $$ 同様に(221.2)、(221.3)を用いれば、 $$ (222.6)=\frac{1-K_{\text{IF,RF}}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_{\mathrm{SM}}(t)R_{\mathrm{IF}}(t)\lambda_{\mathrm{IF}}dt \tag{222.7} $$ これに(104.5)の結果を利用すれば、 $$ (222.7)=(1-K_{\text{IF,RF}})\alpha\tag{222.8} $$ 以上より、IFRモデルの統合、分離方式を比較すると、表222.1のようになります。変化点を黄色で示しています。
| (1)SPF | (2)DPF1 | (3)DPF2 | ||
|---|---|---|---|---|
| LAT2統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$ (103.7) |
$(1-K_\text{IF,RF})\alpha+K_\text{IF,RF}\beta$ (107.8) |
$K_\text{IF,RF}\beta$ (106.4) |
|
| 規格式1(1)+(2)$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\beta$ | |||
| 規格式3(1)+(2)+(3)$\dagger$ | $(1-K_\text{IF,RF})\lambda_\text{IF}+2K_\text{IF,RF}\beta$ | |||
| (1)SPF | (2b)SPF' | (2a)DPF1 | (3)DPF2 | |
| LAT2分離 | $(1-K_\text{IF,RF})\lambda_\text{IF}-(1-K_\text{IF,RF})\alpha$ | $(1-K_\text{IF,RF})\alpha$ (222.7) |
$K_\text{IF,RF}\beta$ (222.5) |
$K_\text{IF,RF}\beta$ |
| (1)+(2b)SPF | (2a)DPF1 | (3)DPF2 | ||
| SPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $K_\text{IF,RF}\beta$ | $K_\text{IF,RF}\beta$ | |
| SPF/DPF統合 | $(1-K_\text{IF,RF})\lambda_\text{IF}$ | $2K_\text{IF,RF}\beta$ | ||
$$ \text{ただし、} \begin{cases} \alpha:=\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{SM,MPF}})T_\text{lifetime}+K_{\mathrm{SM,MPF}}\tau]\\ \beta:=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \end{cases} $$
前稿と同様、SPF統合のほうが単純な式となっています。LAT2統合において、SPFもDPF1も複雑な式でしたが、まとめ方を変えると単純な式となるため、この方が本質だと考えます。
一般式
表222.1より、2020年RAMS論文で示したように一般式は以下のようになります。 $$ M_\text{PMHF}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+2K_\text{IF,RF}\beta}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ s.t.\quad K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \tag{222.9} $$
また、$K_\text{IF,MPF}=0$のとき、すなわち、IFRモデルにおいて、IFの2nd SMが存在せずアンリペアラブルとなるときは$K_\text{MPF}=K_\text{SM,MPF}$となるため、$\beta=\alpha$となり、当然ですがIFRモデルはIFUモデルと同一の式となります。
冗長構成
IFRモデルはIFもSMもリペアラブルということは冗長構成により$K_\text{IF,RF}=1$となるため、それを適用したものを表222.2に示します。SPFが0となるため、LAT2統合でもSPF統合でも
- $M_\text{PMHF,SPF}=0$
- $M_\text{PMHF,DPF1}=\beta$
となり変わりません。
| (1)SPF | (2)DPF1 | (3)DPF2 | ||||
|---|---|---|---|---|---|---|
| LAT2統合 | $0$ | $\beta$ | $\beta$ | |||
| 規格式1(1)+(2)$\dagger$ | $\beta$ | |||||
| 規格式3(1)+(2)+(3)$\dagger$ | $2\beta$ | |||||
| (1)SPF | (2b)SPF' | (2a)DPF1 | (3)DPF2 | |||
| LAT2分離 | $0$ | $0$ | $\beta$ | $\beta$ | ||
| (1)+(2b)SPF | (2a)DPF1 | (3)DPF2 | ||||
| SPF統合 | $0$ | $\beta$ | $\beta$ | |||
| SPF/DPF統合 | $0$ | $2\beta$ | ||||
$$M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}\\ =\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\tag{222.10}$$
$\dagger$規格式1: 規格第1版 Part 10-8.3.3の第1式(ブログの図104.2)の条件=IFが後にフォールトする場合。DPF2はSMが後にフォールトする場合なので対象外
$\dagger$規格式3: 規格第1版 Part 10-8.3.3の第3式(ブログの図105.2)の条件=IF, SMのフォールトの順を問わない場合

Leave a Comment