|
9 |
ISO 26262のFTAに関する論文 (16) |
この結果はワーストケースの評価であり、2nd order SMを無視しているものです。従って、この結果をより実際に近づけるには、2nd order SMのDCをFTに入れる必要があります。
まず、数式で書けば、 $$ \begin{eqnarray} \Pr\{\text{TOP Failure}\}=M_\text{PMHF}\cdot T_\text{L}&=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L}) \left[ (1-K_\text{MPF})+K_\text{MPF}\cdot \frac{\tau}{T_\text{L}} \right]\\ &=&(\lambda_\text{E1}T_\text{L})(\lambda_\text{E2}T_\text{L})C_\text{1, 2} \end{eqnarray} $$ ただし $$ K_\text{MPF}=1-(1-K_\text{E1,MPF})(1-K_\text{E2,MPF}) $$ $C_\text{1, 2}$はE1, E2に依存する定数で、 $$ C_\text{1, 2}\equiv(1-K_\text{MPF})+K_\text{MPF}\cdot \frac{\tau}{T_\text{L}} $$
車両寿命$T_\text{L}=15,000[H]$、定期検査周期$\tau=3,420[H]$として、今回のE1, E2のペアで$C_\text{1, 2}$を計算したところ、表217.1に示すようにC1からC9の9種類の定数が得られました。
| 定数記号 | 定数値 |
|---|---|
| C1 | 0.2280772 |
| C2 | 0.2287720 |
| C3 | 0.2310880 |
| C4 | 0.2357200 |
| C5 | 0.2588800 |
| C6 | 0.3052000 |
| C7 | 0.3515200 |
| C8 | 0.5368000 |
| C9 | 1.0000000 |
よって、2入力AND項にそれぞれこの定数項を加えて3ANDとすれば、図217.1のようなFTとなります。今回はマニュアル作業により付加しましたが、モデルもしくはツールを開発した暁には自動的に計算が行われる見込みです。

このMCSを取得したところ、表217.2の表のような結果となりました。
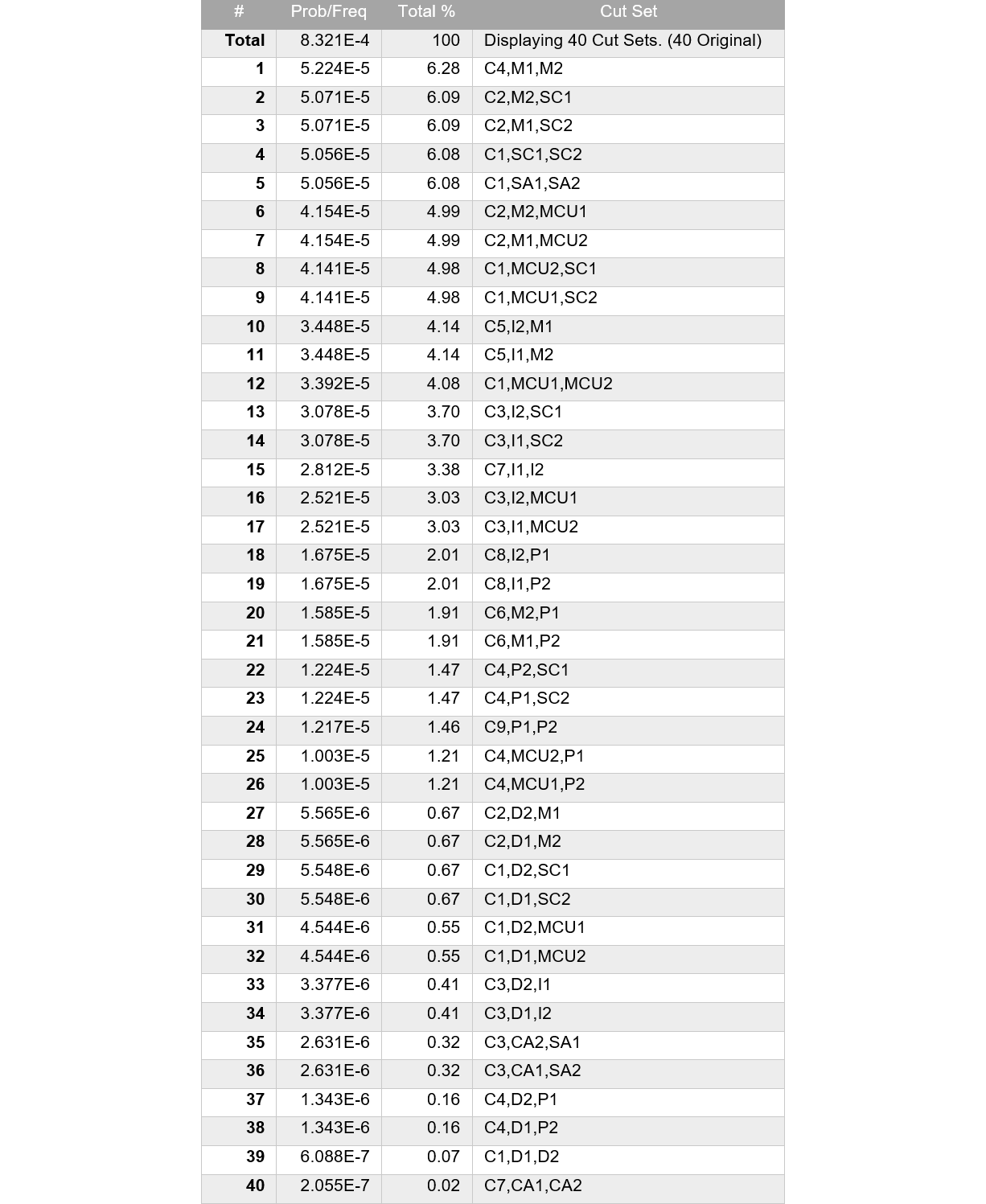
頂上事象侵害確率は$8.321\times 10^{-4}$、PMHFは55.5[FIT]となりました。このように2nd order SMの効果を入れると、PMHFは25%まで低減することがわかります。
RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。
