元に戻って最初の論文を見てみたいと思います。元の論文のFTはLFが考慮されていないものでした。これに対して、前稿において、ワーストケース評価をするため、2nd SMのDC(Diagnostic Coverage)をゼロとして評価しました。

これに対して2nd SMのDCを考慮したらどうなるかを前稿と同様の考え方でやってみます。数式やFTの書き換えルールは基本的に前稿を踏襲しますが、IFUモデルとIFRモデルで数式が異なります。いずれにせよ、$K_\text{SM,MPF}=0$とおいたところに仮に$K_\text{SM,MPF}=0.6$と仮定して計算します。

すると、係数$C_\text{SM,MPF}=0.5368$となり、この係数をEBMとOn-line monitorのDPF項に掛けることになるため、そのFTは図219.1のようになります。

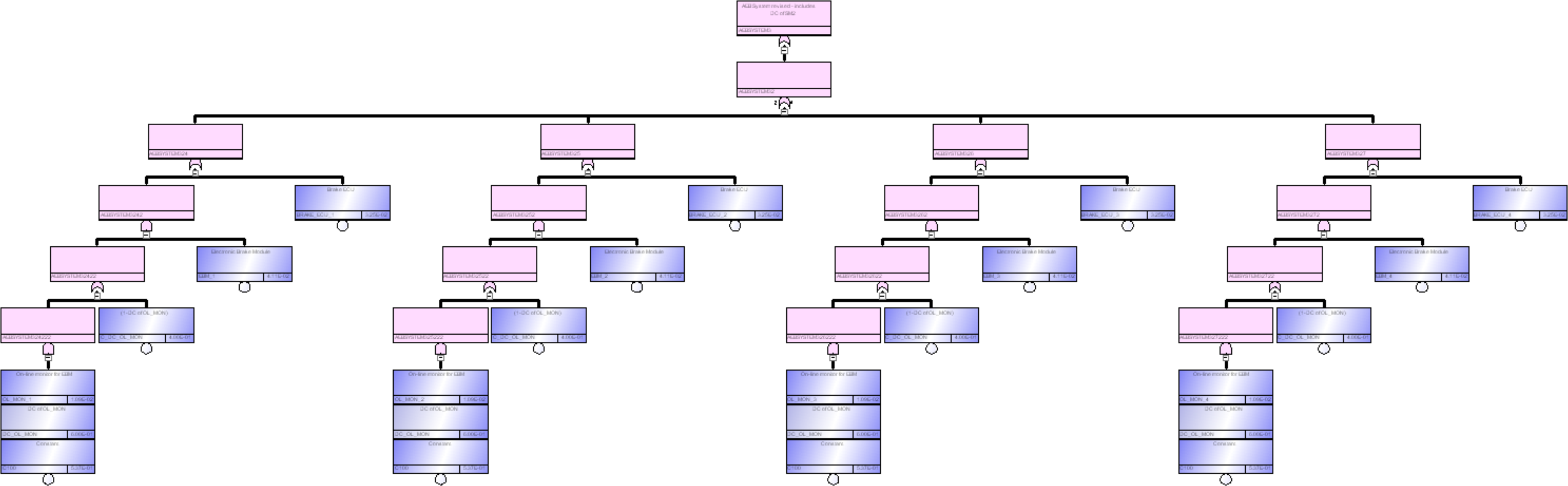
図219.2に図219.1のFTの拡大図を示します。C100として上記係数0.5368をかけています。

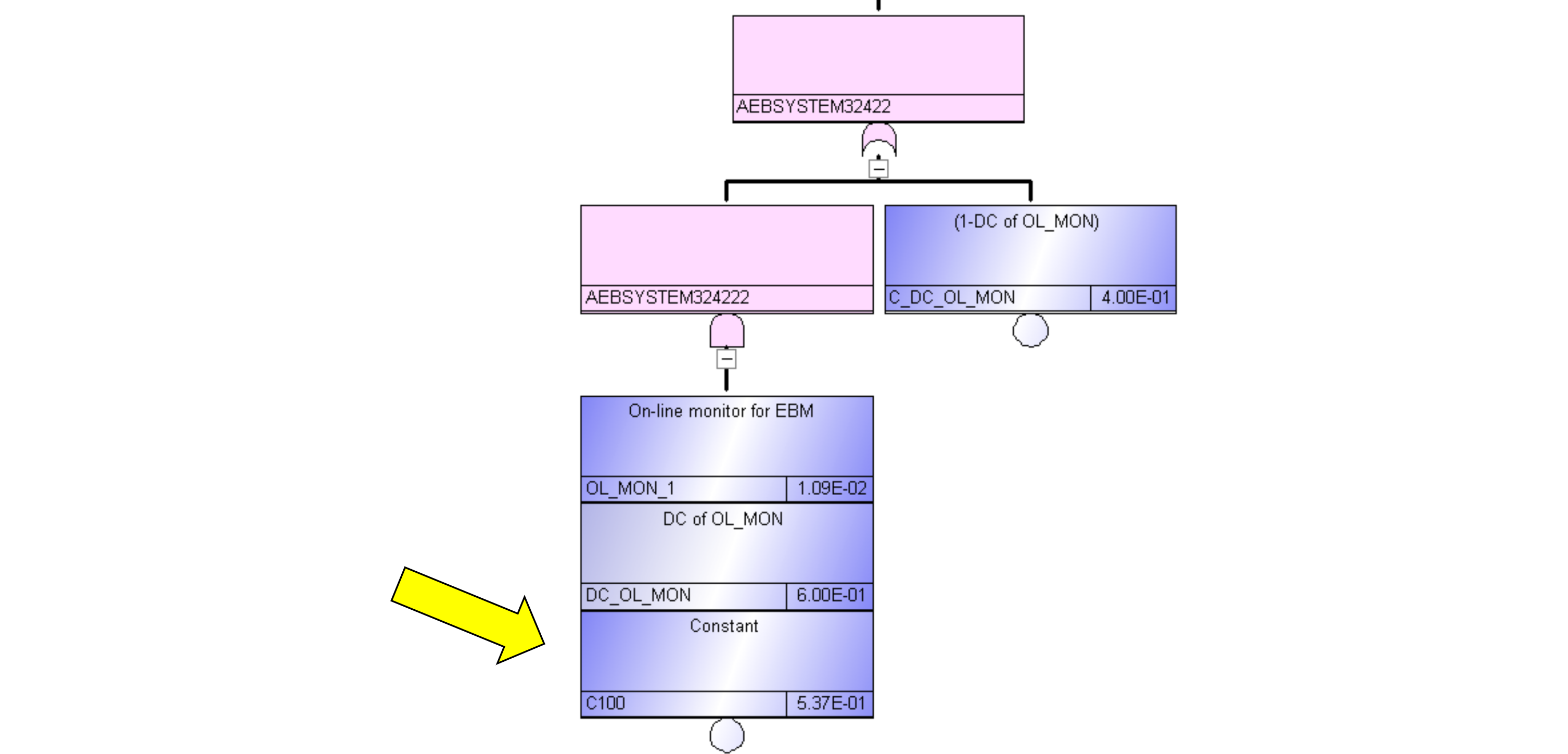
MCS分析を実施すると、42個のMCが得られ、3個以上のエレメント故障をカットすると、24個のMCが残ります。結果として、全く変化はありませんでした。

今回カットされた積項を表219.1に示します。加えた定数(赤字)は全て3点故障以上の積項に掛けられており、全てカットされています。ただし、カットされた積項は18個のはずですが、ツールのバグか17個となっています。

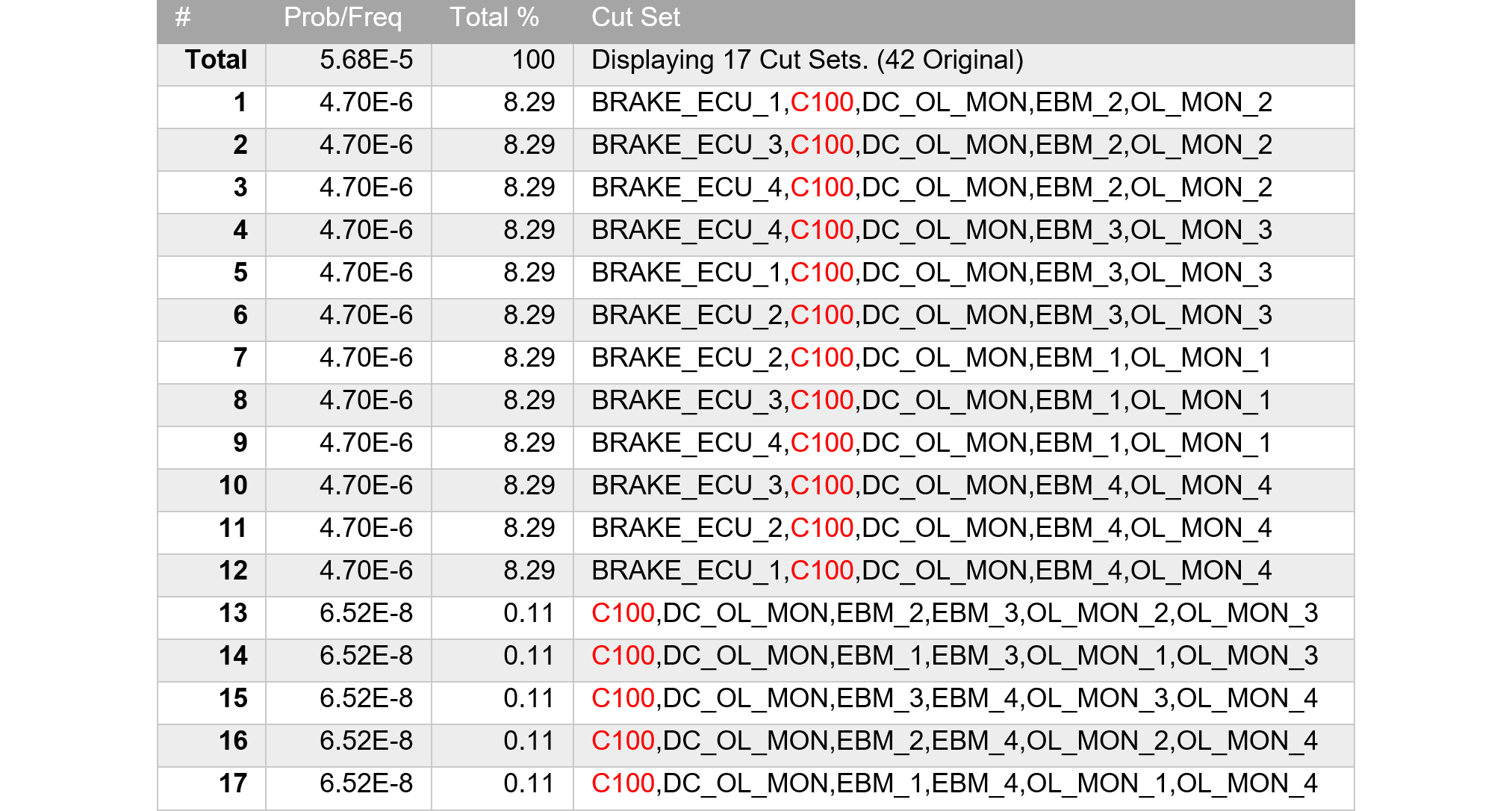
得られたMCSを表219.2に示します。エレメント故障は2以下のみであり、定数を青字で示しています。

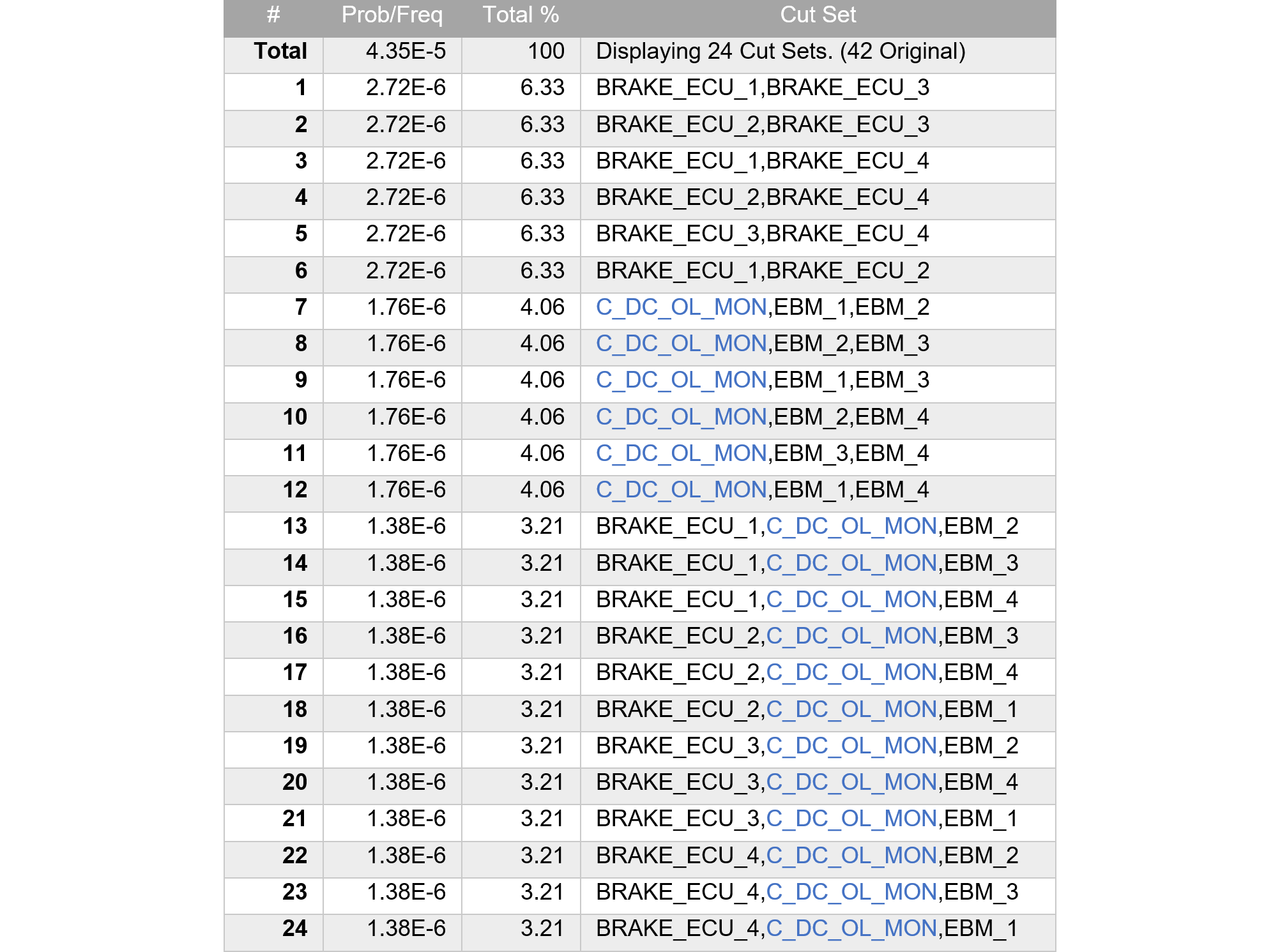
元々2 outof 4という変則的な2冗長内部のSMなので、IFとSMのANDはそれだけで4エレメント故障の積項となります。従って、この積項に何を追加しても元々消えるべき項でした。

RAMS 2021において、PMHF式に基づくFTA構築法の論文発表が終了したため、本記事を開示します。

前のブログ 次のブログ