|
18 |
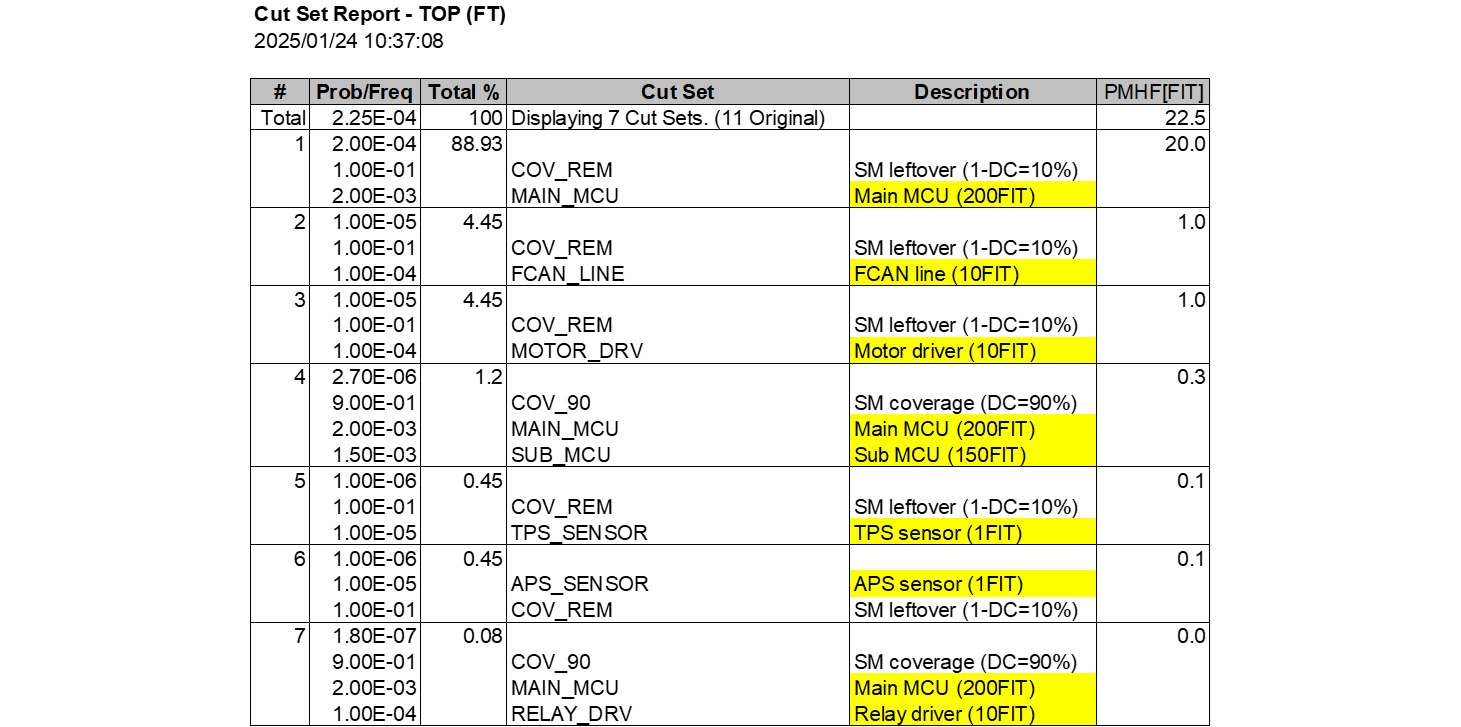
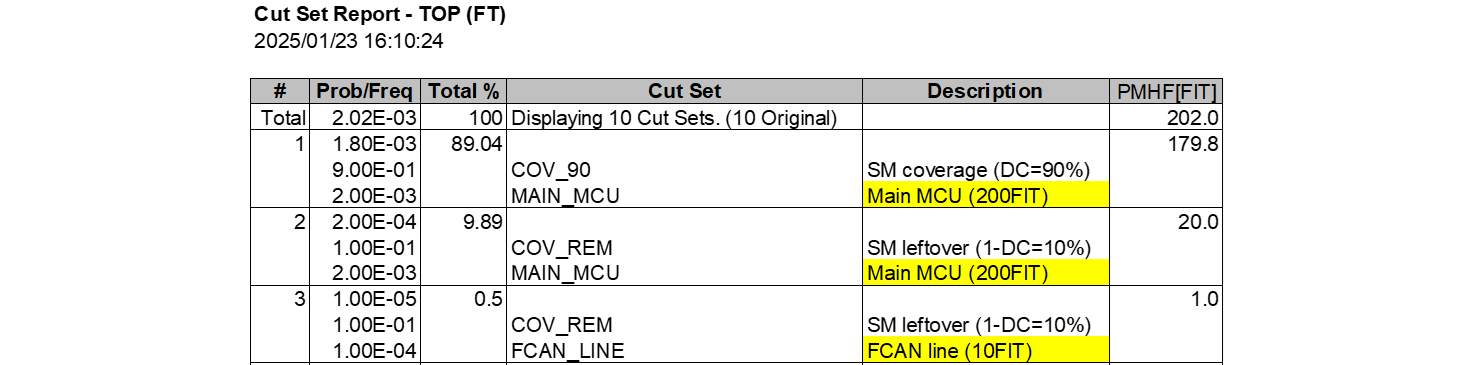
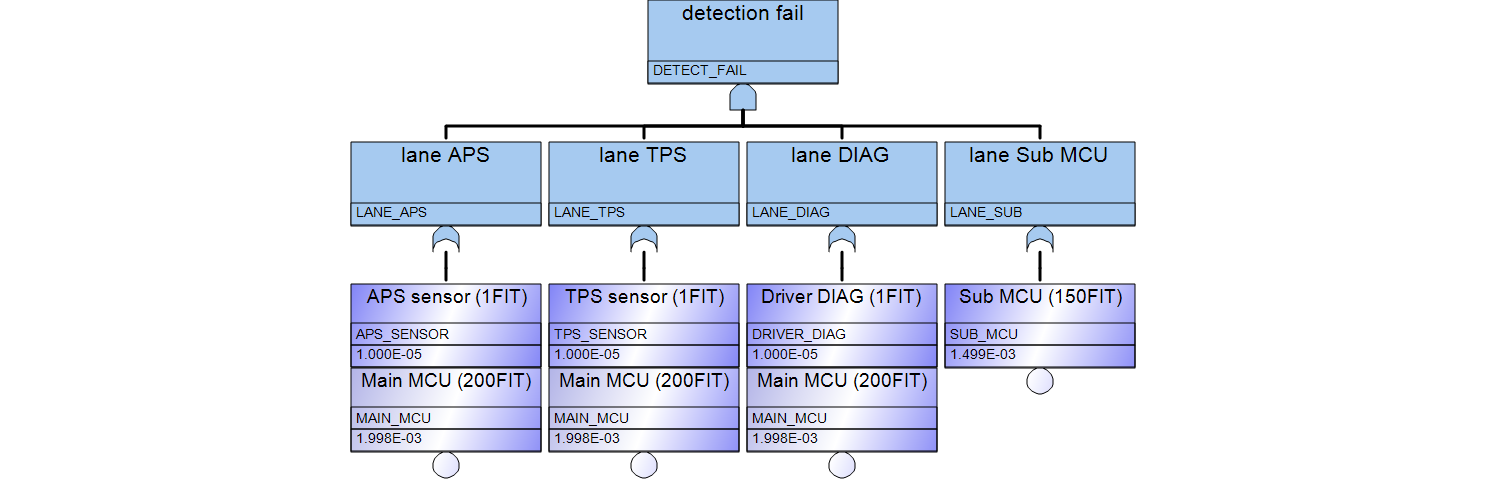
Fault treeの自動生成 (32) |
そもそもEGASアーキテクチャはメインマイコンが主機能を担当し、サブマイコンはメインマイコンのモニタ的な扱いです(EGASの2チャンネル構成の意義)。そこから考えると案1と案4では得失はどうでしょうか?
ChatGPT
以下では、EGAS の 2 チャンネル構成において「メインマイコンが主機能 (IF) を担当し、サブマイコンはモニタ的な扱いである」という前提のもと、案1(サブマイコンが幅広く異常検出 & リレー直接制御) と 案4(サブマイコンはメインマイコン死活を監視し、故障時にリレーを直接制御) について得失を整理します。
案1: サブマイコンが幅広く検出し、リレーを直接制御
誰が検出?
- サブマイコンが APS, TPS, Driver Diag などメインのセンサ情報も取り込むか、少なくとも同様の情報を並列でもらう。
- メインマイコンが主機能を担当していても、サブマイコンがセンサを「モニタ的」にフル読みしている場合には、サブマイコンが完全なバックアップルートを形成。
誰がリレーをオフ?
- サブマイコンが単独で Relay Driver を直接駆動しリレーを切る。
メリット
- サブマイコンが主機能と同レベルでセンサを取得 → メインマイコン故障や誤動作のみならず、「APS/TPS故障」自体もサブマイコンが独立に検出し、リレーOFFできる。
- 故障検出の並列度が高い (メイン・サブそれぞれが全センサを見ている) → 異常検出カバレッジを拡大しやすい。
デメリット
- モニタ的アーキテクチャ以上に大きなソフトウエア負担** → サブマイコン側もAPS/TPS等の取得ロジックや診断フローを実装。
- 「メインマイコンが主機能担当」というEGAS設計思想からすると、サブマイコンにセンサ処理を大きく複製するのはオーバースペックになる場合がある。
案4: サブマイコンが主に「メインマイコン故障」を監視し、故障時にリレーを直接制御
誰が検出?
- サブマイコンはメインマイコン(および一部限られた診断線)をウォッチして「メインマイコンが固まった/故障している」ことを検出。
- APS/TPSなどの主センサ異常は基本メインマイコンが担当し、サブマイコンはそこまでは見ない(あるいは簡易モニタ程度)。
誰がリレーをオフ?
- サブマイコンがメインマイコンを経由せずリレーを制御 → メインが死んでもサブマイコンがオフ可能。
メリット
- モニタ的なサブマイコンの立ち位置を大きく変えない → 「主機能はメインマイコンが行う」EGASの設計思想を守る。
- ソフト負担が比較的軽い → サブマイコンはメインマイコンの死活監視が中心。APS/TPSなどの大きな計算や詳細診断をサブマイコンで実装しなくてよい。
- メインマイコンに異常があったときのみ “非常停止” できる → 最低限の安全保証は確保。
デメリット
- 「APS/TPSなどセンサ異常」まではサブマイコンが検出せず → メインマイコンが誤検知や故障を起こすと、サブマイコン視点では「メインマイコンが動いているかどうかしかわからない」ため、センサ異常をメインマイコンが見逃したら、サブマイコンがカバーできない。
- Driver Diagもメインマイコン側で見ている構成だと、サブマイコンはそれを直接見ないため、Driver Diagの異常がメインで見逃されたら危険残る。
得失の比較
| 項目 | 案1 | 案4 |
|---|---|---|
| サブマイコンの役割 | 幅広いセンサ検出 (APS/TPS/Driver Diag 等) + リレー制御 | 主にメインマイコン死活監視+簡易モニタ(故障でリレーOFF) |
| ソフト負担 | 大きい(サブマイコンがセンサ処理を重複実装) | 比較的軽い(メイン死活監視+リレー制御ルーチン程度) |
| 主機能 vs モニタ | サブマイコンが主機能のバックアップとして十分機能できる | メインマイコンが主機能、サブマイコンはあくまで死活監視メイン |
| 検出カバレッジ拡大 | しやすい(サブマイコンがAPS/TPS等を独立に見られる) | メインマイコン故障時だけはカバーするが、APS/TPS異常はメイン依存 |
| EGAS思想への整合 | やや大きく変更(サブマイコンがほぼ主機能並みに働く) | 従来の「主機能=メイン、モニタ=サブ」の思想を大きく崩さない |
| コスト面 | 追加ハードは不要だがソフト大幅改修の可能性あり | 追加ハード不要、ソフト改修は監視部とリレー制御のみ |
結論
- 案1 と 案4 はどちらも「メインマイコンが死んでもサブマイコンでリレーをOFF可能」となるが、
- 案1 はサブマイコンが「APS/TPS/DriverDiag」等もフルカバーし、故障を幅広く検出 → サブマイコンが主機能に近い。
- 案4 は「サブマイコンはメインマイコン故障の監視が中心、センサ大半はメインが担当 → ソフト負担軽」 → EGASの“主=メイン / モニタ=サブ”構造を保ちやすい。
EGASアーキテクチャで「メインマイコンが主機能/サブはモニタ」の大枠をあまり崩したくないなら、案4 がより自然。一方、サブマイコンが本格的にAPS/TPS等を独立処理できるなら案1の安全度は高いが、システム変更が大きい。
よって案4はEGASの2チャンネル構成を大きく変えずに「メインマイコン死活監視 → リレー直接制御」を追加するだけで済むため、最もEGAS思想に近く、低コストでメインマイコン故障をカバーできると言えます。
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。
ユーザとの会話により、ChatGPTの結論としてユーザ提案回路と同一となったものの、その道のりにはいろいろなポイントが含まれており、なかなか示唆に富む会話だったと思います。
なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。