最初にSM1に、次にIFにフォールトが起きた場合
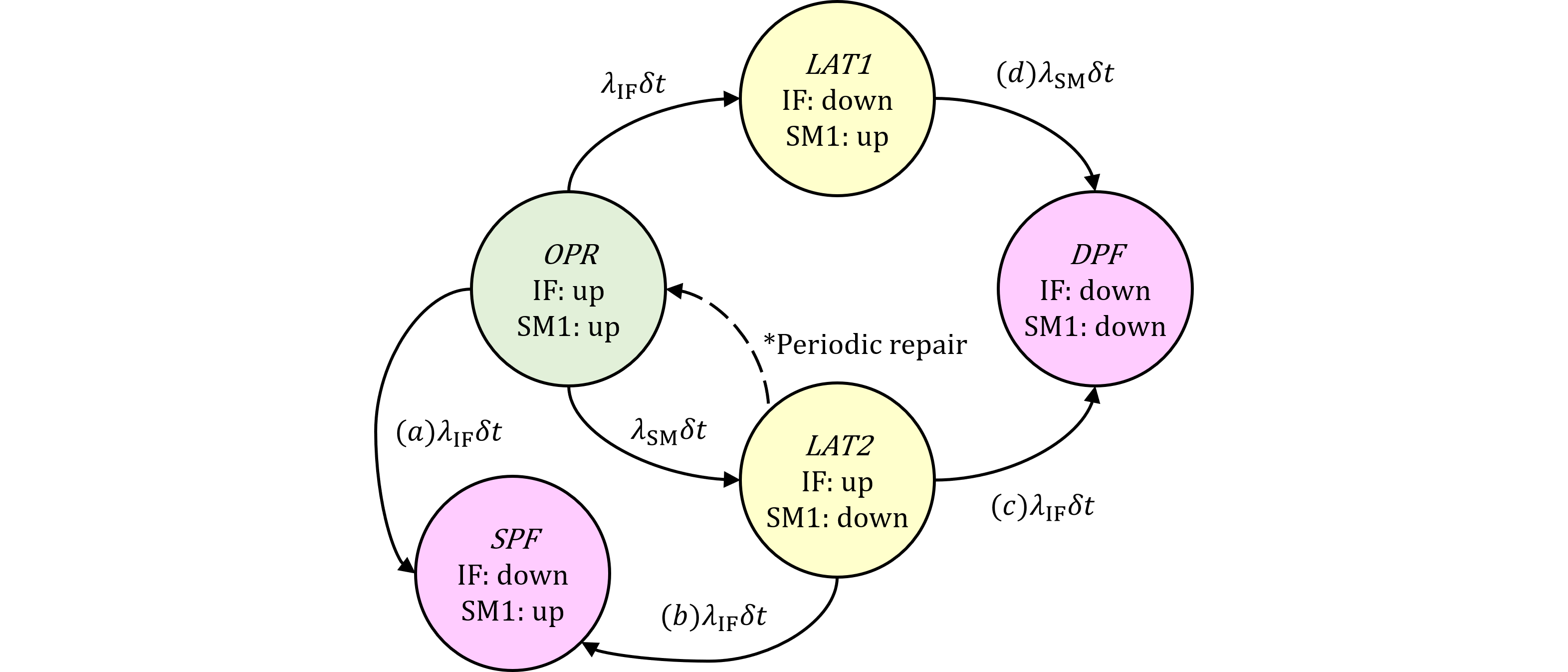
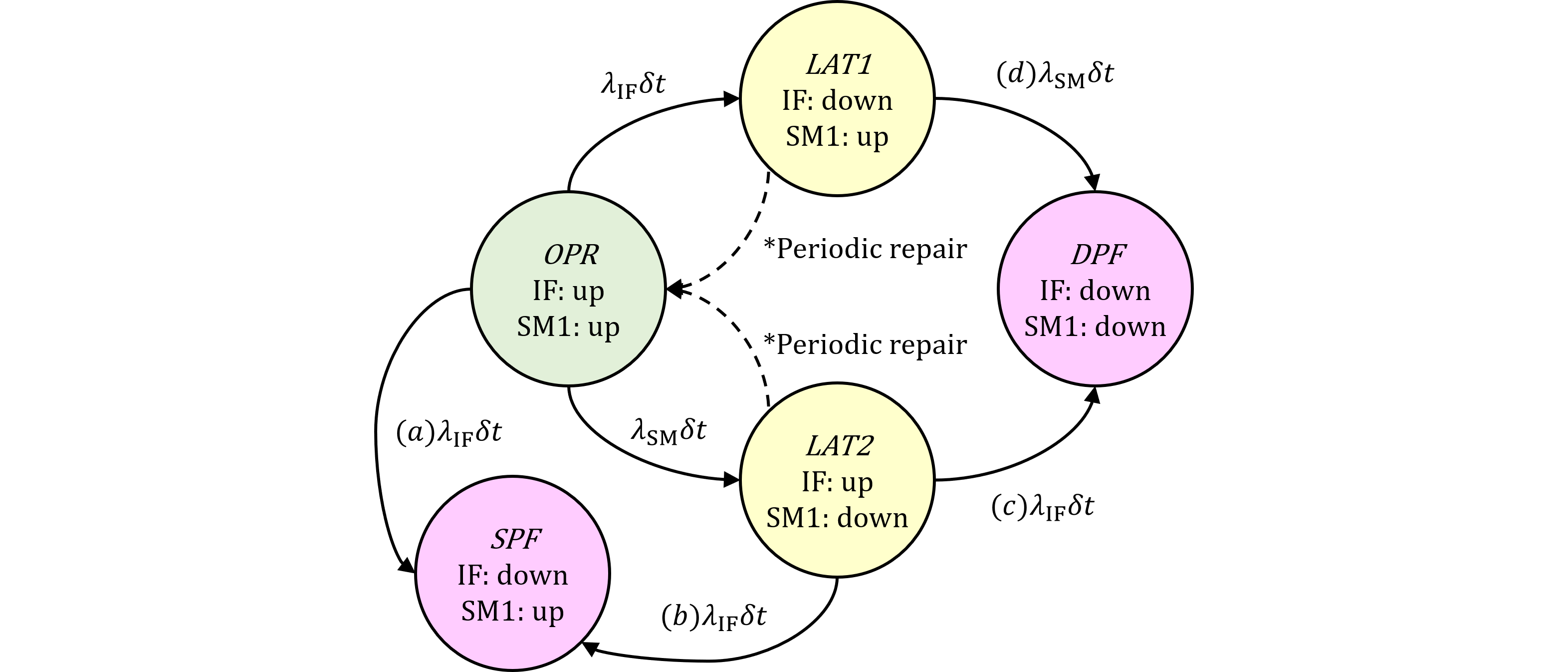
図487.2にIFUモデルのCTMCを示します。IFUモデルは最初のSM1のフォールトがリペアラブル、2番目のIFのフォールトがアンリペアラブルです。※便宜上「最初」と「2番目」と記述しましたが、厳密には「最後から2番目」と「最後」です。
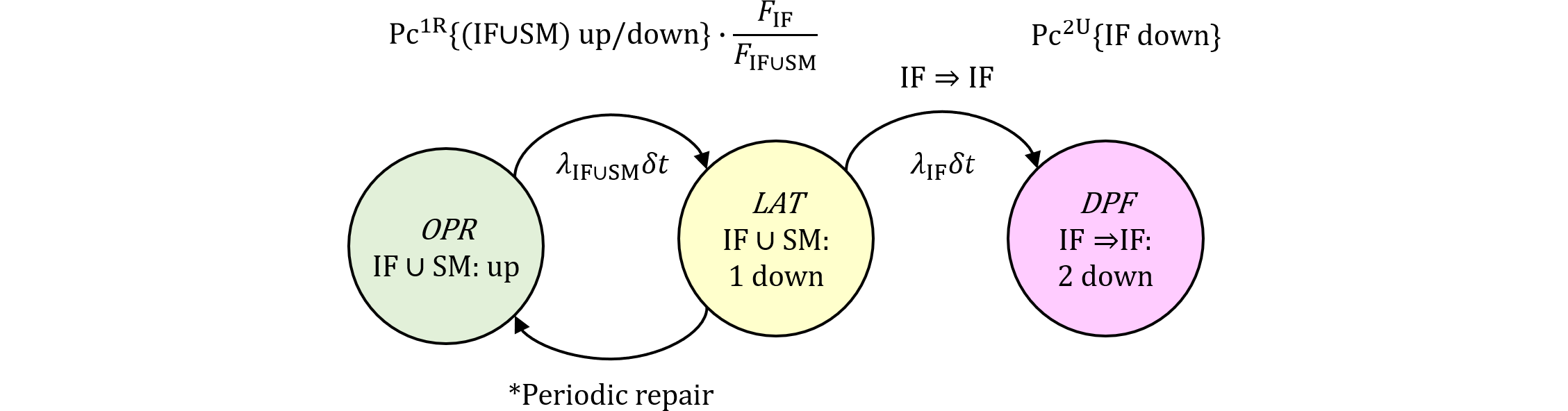
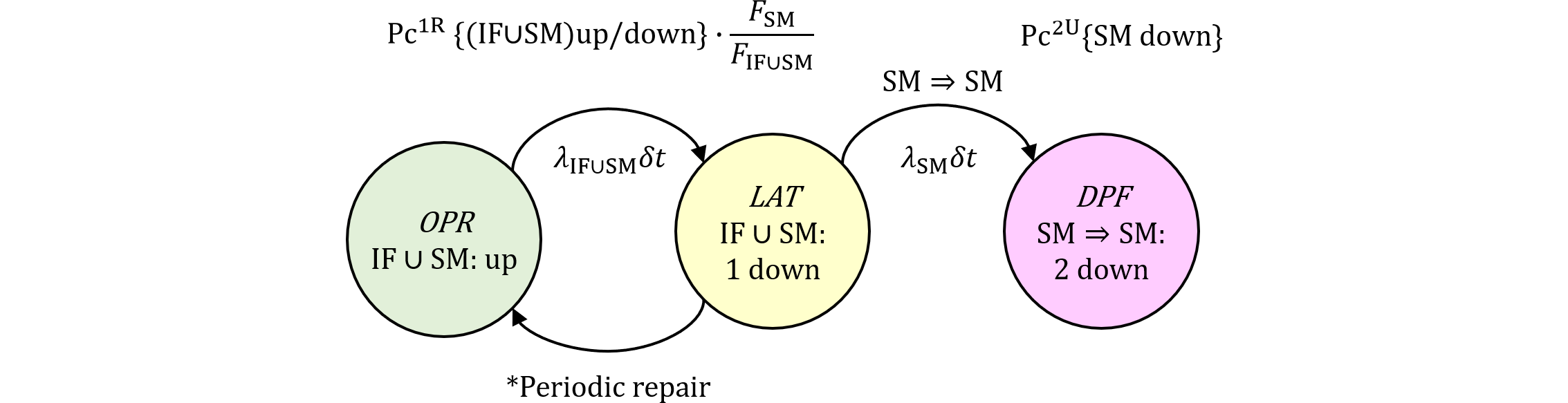
 図487.1 IFUモデルのマルコフ連鎖
図487.1 IFUモデルのマルコフ連鎖
CTMCによるPMHFの導出
(1st Editionの)規格第1式のPMHF式のDPF項の導出は以下の(487.1)のとおり、遷移確率と状態確率を掛けた確率微分方程式を車両寿命間で積分することにより導出します。
$$
\begin{eqnarray}
M_\text{PMHF,DPF}&=&\overline{q_\mathrm{DPF,IFU}}\\
&=&\frac{1}{T_\text{lifetime}}\Pr\{DPF\mathrm{\ at\ }T_\text{lifetime}\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{LAT\mathrm{ at\ }t\cap\mathrm{IF^U\ down\ in\ }(t, t+dt]\cap\mathrm{IF\ preventable}\}\\
&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF^U\ down\ in\ }(t, t+dt]\ |\ LAT\mathrm{\ at\ }t\}\\
& &\ \ \ \ \cdot\Pr\{LAT\mathrm{ at\ }t\}\Pr\{\mathrm{IF\ preventable}\}\\
&=&\frac{K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}Q_\mathrm{SM}(t)R_\mathrm{IF}(t)\lambda_\mathrm{IF}dt\\
&=&\frac{K_\text{IF,RF}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-K_\mathrm{SM,DPF})F_\mathrm{SM}(t)+K_\mathrm{SM,DPF}F_\mathrm{SM}(t\bmod\tau)\right]f_\mathrm{IF}(t)dt,\\
&\approx&\frac{1}{2}K_\mathrm{IF,RF}\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{SM,DPF})T_\text{lifetime}+K_\mathrm{SM,DPF}\tau]
\end{eqnarray}
\tag{487.1}
$$
となります。これには弊社の積分公式を用いています。このPMHF式は1st editionのPMHF第1式と完全に一致します。
PMHFを第1、第2確率コントリビューションに分解
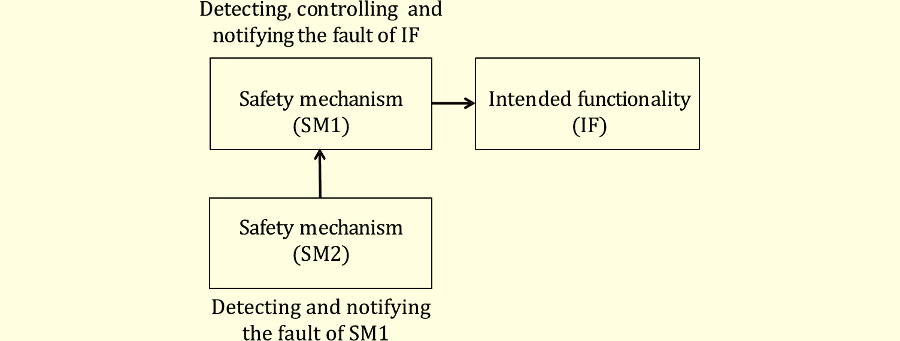
このPMHFをIFとSM1の第1及び第2確率コントリビューションに分解します。第1及び第2確率コントリビューション$\text{Pc}^\text{1R}$及び$\text{Pc}^\text{2U}$は確率ではありませんが、掛け合わせてPMHFに貢献する要素です。
SM1を$e1$: repairable 1st fault elementと置き、IFを$e2$: unrepairable 2nd fault elementと置けば(487.1)は、
$$
M_\text{PMHF,DPF}=\frac{1}{2T_\text{lifetime}}\text{Pc}^\text{1R}\{e1\text{ up/down}\}\text{Pc}^\text{2U}\{e2\text{ down}\}\\
=\frac{1}{2T_\text{lifetime}}\lambda_\mathrm{e1}[(1-K_\mathrm{e1,DPF})T_\text{lifetime}+K_\mathrm{e1,DPF}\tau]\cdot K_\mathrm{e2,RF}\lambda_\mathrm{e2}T_\text{lifetime}
\tag{487.2}
$$
と書けます。確率コントリビューションは単独では意味を持たず、(487.2)のDPF積の場合にのみ使用します。
ここで、(487.2)において、$K_\mathrm{e1,DPF}$はe1のLF検出率であり、それぞれ、
$$
\begin{cases}
1-K_\mathrm{e1,DPF}=\Pr\{\overline{e1\text{ detected}}\}\\
K_\mathrm{e1,DPF}=\Pr\{e1\text{ detected}\}
\end{cases}
\tag{487.3}
$$
と書けます。また(487.2)において、$K_\mathrm{e2,RF}$は、e2のVSG prevented確率であるため、
$$
K_\mathrm{e2,RF}=\Pr\{e2\text{ prevented}\}\tag{487.4}
$$
と書けます。
よって$e1$と$e2$の確率コントリビューションは、第1と第2がそれぞれ、
$$
\begin{cases}
\text{Pc}^\text{1R}\{e1\text{ up/down}\}:=
\lambda_{e1}(\Pr\{\overline{e1\text{ detected}}\}T_\text{lifetime}+\Pr\{e1\text{ detected}\}\tau)\\
\text{Pc}^\text{2U}\{e2\text{ down}\}:=
\Pr\{e2\text{ prevented}\}\lambda_{e2}T_\text{lifetime}
\tag{487.5}
\end{cases}
$$
と定義されます。
なお、本稿はRAMS 2023に投稿中のため一部を秘匿していますが、論文公開後の2023年2月頃に開示予定です。RAMS 2023が終了したため、秘匿部分を開示します。
 前のブログ
次のブログ
前のブログ
次のブログ