IFとSMのユニオンエレメント$\text{IF}\cup\text{SM}$を考えます。PMHFのDPFに関する第1確率コントリビューションは、 $$ \text{Pc}^\text{1R}\{\mathrm{(IF\cup SM)\ up/down}\}: \tag{489.1} $$ となり、第2確率コントリビューションは、 $$ \text{Pc}^\text{2U}\{\text{(IF}\cup\text{SM) down}\}:=K_\text{IF,RF}(\lambda_\text{IF}+\lambda_\text{SM})T_\text{lifetime} \tag{489.2} $$ と定義されます。これらの積からDPFのPMHFを作成したいのですが、問題は以下の2つのケースを除く必要があることです。

　①IFのフォールトに引き続いてIFのフォールト、及び、
　②SM1のフォールトに引き続いてSM1のフォールト

理由は、同じエレメントの引き続くフォールトではDPFとならないからです。それぞれの確率コントリビューションのマルコフ図は、

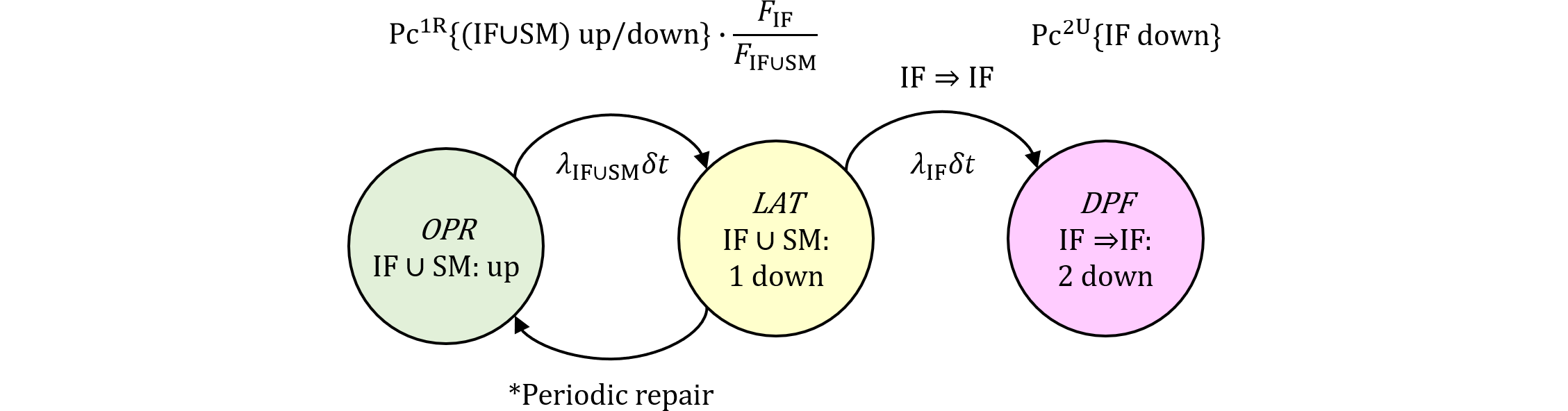
図489.1において、OPR⇒LAT⇒OPRを繰り返している間はIF$\cup$SM、すなわちIFかSMかのいずれかのフォールトが起きますが、LAT⇒DPFの遷移の場合のみ、IFがダウンしている場合にIFのフォールトが起きる事象です。

従って、合成エレメントの第1確率コントリビューションの$\text{Pc}^\text{1R}$は$\text{IF}\cup\text{SM}$の最後の状態において、$\text{IF}\cup\text{SM}$の不信頼度のところを、IFのみの不信頼度に減らす必要があります。他方、第2確率コントリビューションの$\text{Pc}^\text{2U}$は、エレメントはIFのみとすれば良いわけです。従って、減少分も含めた第1確率コントリビューションは、時刻$t$で第2フォールトが起きるとして、 $$ \require{color} \definecolor{yellow}{rgb}{1.0,1.0,0.7} \require{cancel} \text{Pc}^\text{1R}\{\mathrm{(IF\cup SM)\ up/down}\}\cdot\bbox[#ffffcc,2pt]{\frac{Q_\text{IF}(t)}{Q_{\text{IF}\cup\text{SM}}(t)}} \approx\text{Pc}^\text{1R}\{\mathrm{(IF\cup SM)\ up/down}\}\bbox[#ffffcc,2pt]{\frac{F_\text{IF}(t)}{F_{\text{IF}\cup\text{SM}}(t)}}\\ \approx(\lambda_\text{IF}+\lambda_\text{SM})[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \bbox[#ffffcc,2pt]{\frac{\lambda_\text{IF}\bcancel{t}}{\lambda_\text{IF}\bcancel{t}+\lambda_\text{SM}\bcancel{t}}}\\ =\bcancel{(\lambda_\text{IF}+\lambda_\text{SM})}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \bbox[#ffffcc,2pt]{\frac{\lambda_\text{IF}}{\bcancel{\lambda_\text{IF}+\lambda_\text{SM}}}}\\ =\lambda_\text{IF}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{489.3} $$ となり、第2確率コントリビューションはIFのみなので、 $$ \text{Pc}^\text{2U}\{\text{IF down}\}=K_\text{IF,RF}\lambda_\text{IF}T_\text{lifetime} \tag{489.4} $$ となります。従って、これらをかけ合わせれば除外するPMHFは、 $$ M_\text{PMHF,DPF,IF⇒IF} =\frac{K_\text{IF,RF}}{2}\lambda_\text{IF}^2[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{489.5} $$ となります。

全く同様に、SM⇒SMに関する確率コントリビューションのマルコフ図は、

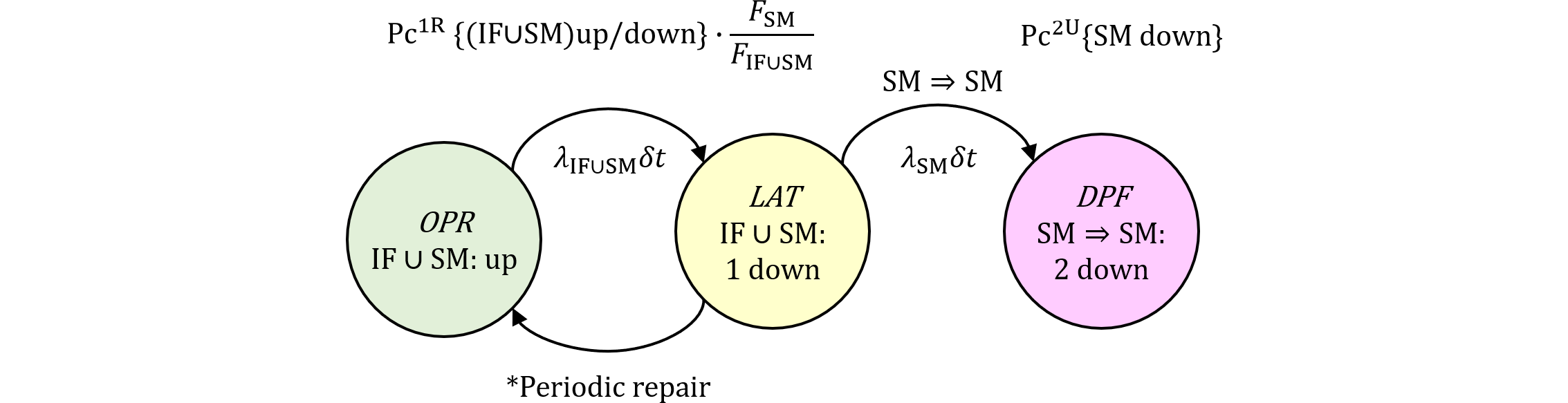
同様に、減少分も含めた第1確率コントリビューションは、 $$ \require{cancel} \text{Pc}^\text{1R}\{\mathrm{(IF\cup SM)\ up/down}\}\cdot\bbox[#ffffcc,2pt]{\frac{Q_\text{SM}(t)}{Q_{\text{IF}\cup\text{SM}}(t)}}\\ \approx\lambda_\text{SM}[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{489.6} $$ となり、第2確率コントリビューションはSMのみなので、 $$ \text{Pc}^\text{2U}\{\text{SM down}\}=K_\text{IF,RF}\lambda_\text{SM}T_\text{lifetime} \tag{489.7} $$ となります。従って、これらをかけ合わせれば除外するPMHFは、 $$ M_\text{PMHF,DPF,SM⇒SM} =\frac{K_\text{IF,RF}}{2}\lambda_\text{SM}^2[(1-K_\mathrm{DPF})T_\text{lifetime}+K_\mathrm{DPF}\tau] \tag{489.8} $$ となります。

なお、本稿はRAMS 2023に投稿中のため一部を秘匿していますが、論文公開後の2023年2月頃に開示予定です。RAMS 2023が終了したため、秘匿部分を開示します。

前のブログ 次のブログ