*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue, Prob, Lambda, Tau, Mission, Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
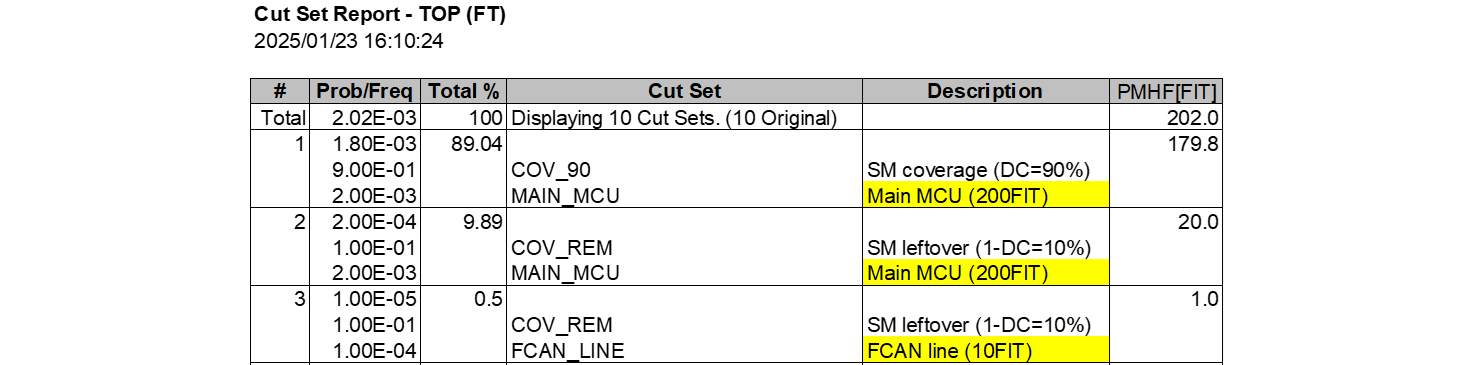
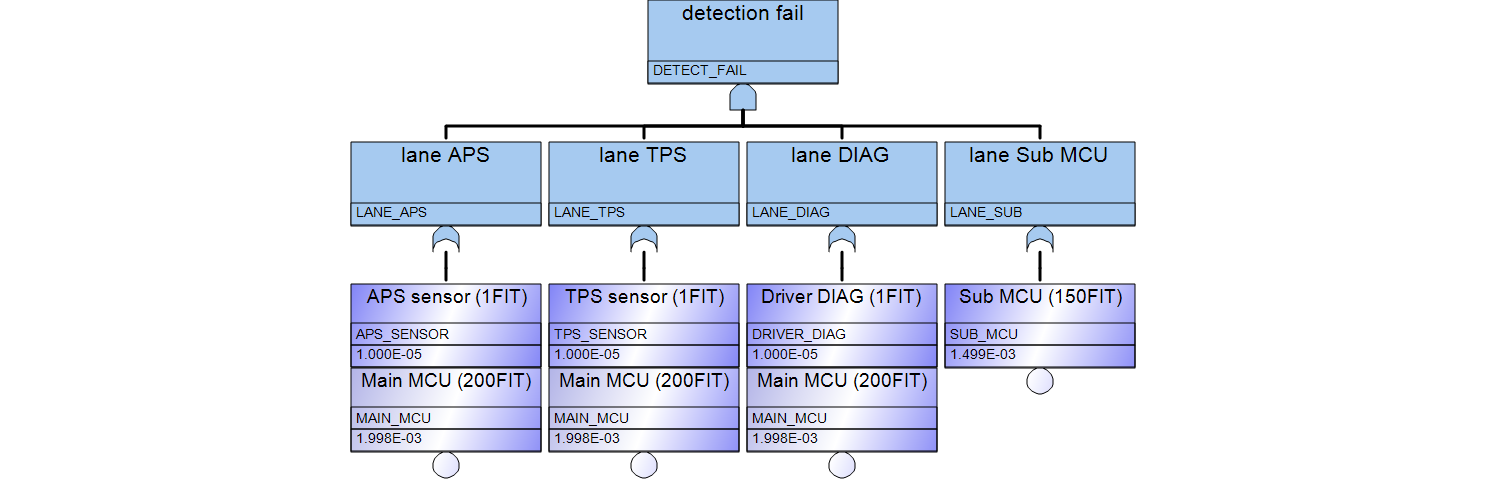
APS_SENSOR ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
TPS_SENSOR ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
FCAN_LINE ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
MAIN_MCU ,3, , , , ,2.0E-007, ,1.0E+004, , , ,2.0E-003, ,RANDOM,CD,TEST
MOTOR_DRV ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
DRIVER_DIAG ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
SUB_MCU ,3, , , , ,1.5E-007, ,1.0E+004, , , ,1.5E-003, ,RANDOM,CD,TEST
RELAY_DRV ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
COV_REM ,1, , , ,1.0E-001, , , , , , ,1.0E-001, ,RANDOM,CD,TEST
COV_90 ,1, , , ,9.0E-001, , , , , , ,9.0E-001, ,RANDOM,CD,TEST