|
16 |
Fault treeの自動生成 (19) |
 |
ChatGPTにRBDを示してFTを生成させます。まず基本形のRBDを図930.1に示します。
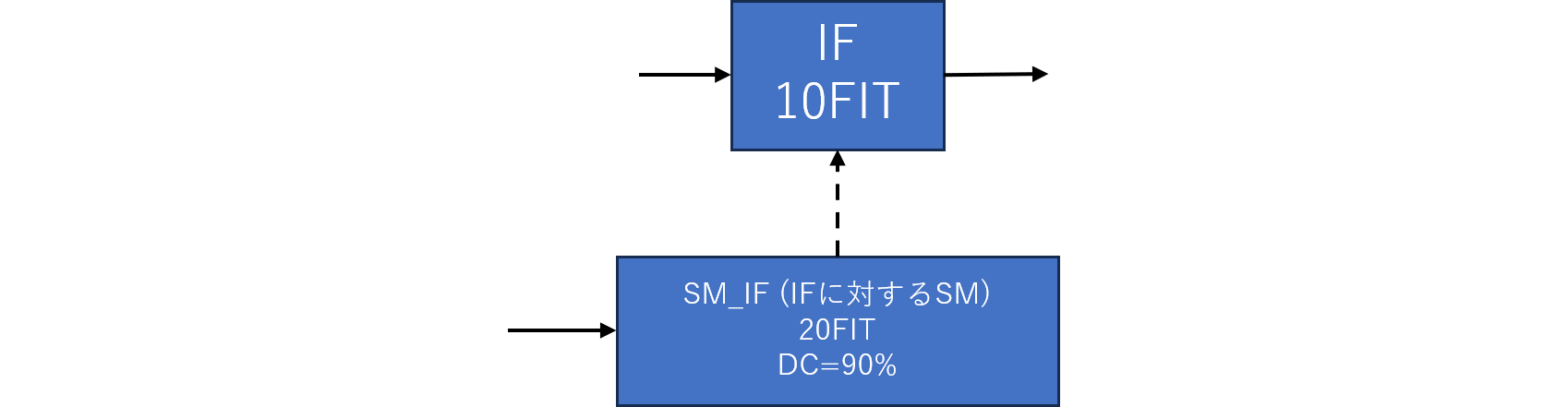
ここでは2nd SMは省略しています。その理由はワーストケース評価を行いたいためです。冗長系ではRFがほとんど存在しないため、2nd SMの効果が大きく見えてきますが、このような非冗長系においては1st SMの効果であるRFが支配的であり、経験からはRFは95%以上となる場合が多いと考えます。
図930.1を読み取ったChatGPTの生成したMARDファイルを以下に示します。
TEST.BED
*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
IF_FAULT , IF fault(10FIT) , TEST
SM_FAULT , SM_IF fault(20FIT) , TEST
SM_IF_COVREM , SM_IF coverage leftover(1-DC=10%) , TEST
SM_IF_COV , SM_IF coverage(DC=90%) , TEST
TEST.BEI
*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue, Prob, Lambda, Tau, Mission, Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
IF_FAULT ,3, , , , ,1.0E-008, ,1.0E+005, , , ,1.0E-003, ,RANDOM,CD,TEST
SM_FAULT ,3, , , , ,2.0E-008, ,1.0E+005, , , ,2.0E-003, ,RANDOM,CD,TEST
SM_IF_COVREM ,1, , , ,1.0E-001, , , , , , ,1.0E-001, ,RANDOM,CD,TEST
SM_IF_COV ,1, , , ,9.0E-001, , , , , , ,9.0E-001, ,RANDOM,CD,TEST
TEST.FTD
TEST =
* Name , Description, SubTree, Alternate, Project
TOP , TEST , , , TEST
TEST.FTL
TEST, TOP =
TOP AND IF_FAULT SM_IF
SM_IF OR SM_IF_COVREM DPF
DPF AND SM_IF_COV SM_FAULT
TEST.GTD
TEST=
* Name , Description, Project
TOP , TEST , ,TEST
SM_IF , SM_IF gate , ,TEST
DPF , coverage partial path , ,TEST
図930.2にこれらのMARDをSpahireにロードし生成したFTを示します。
$$\img[-1.35em]{/images/withinseminar.png}$$
比較のために前記事に掲載した基本形のFT図$\dagger$を示します。
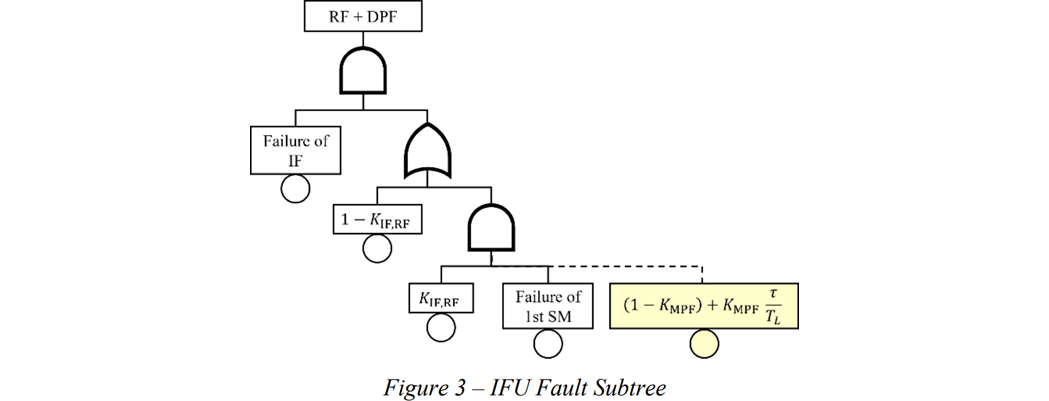
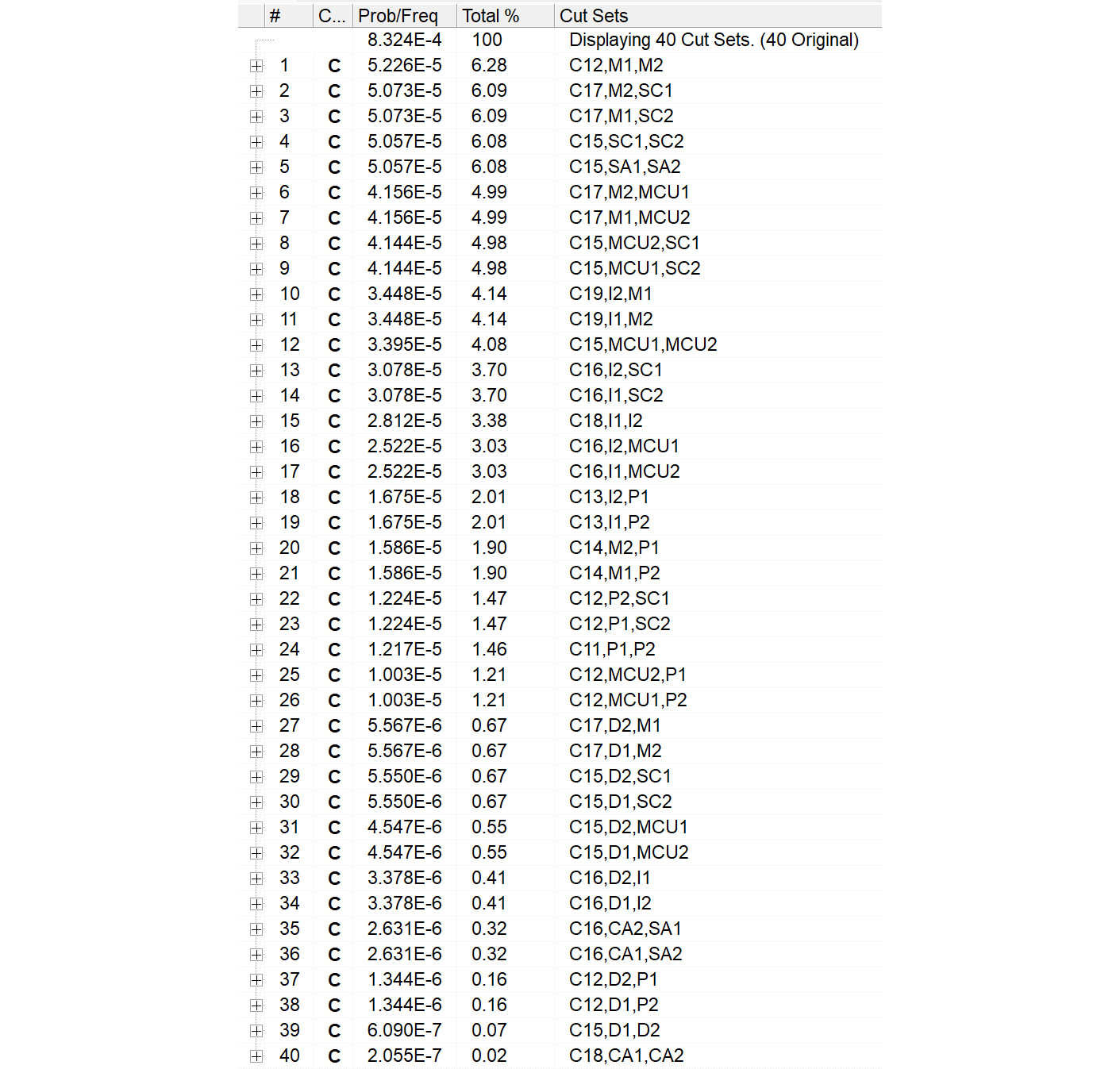
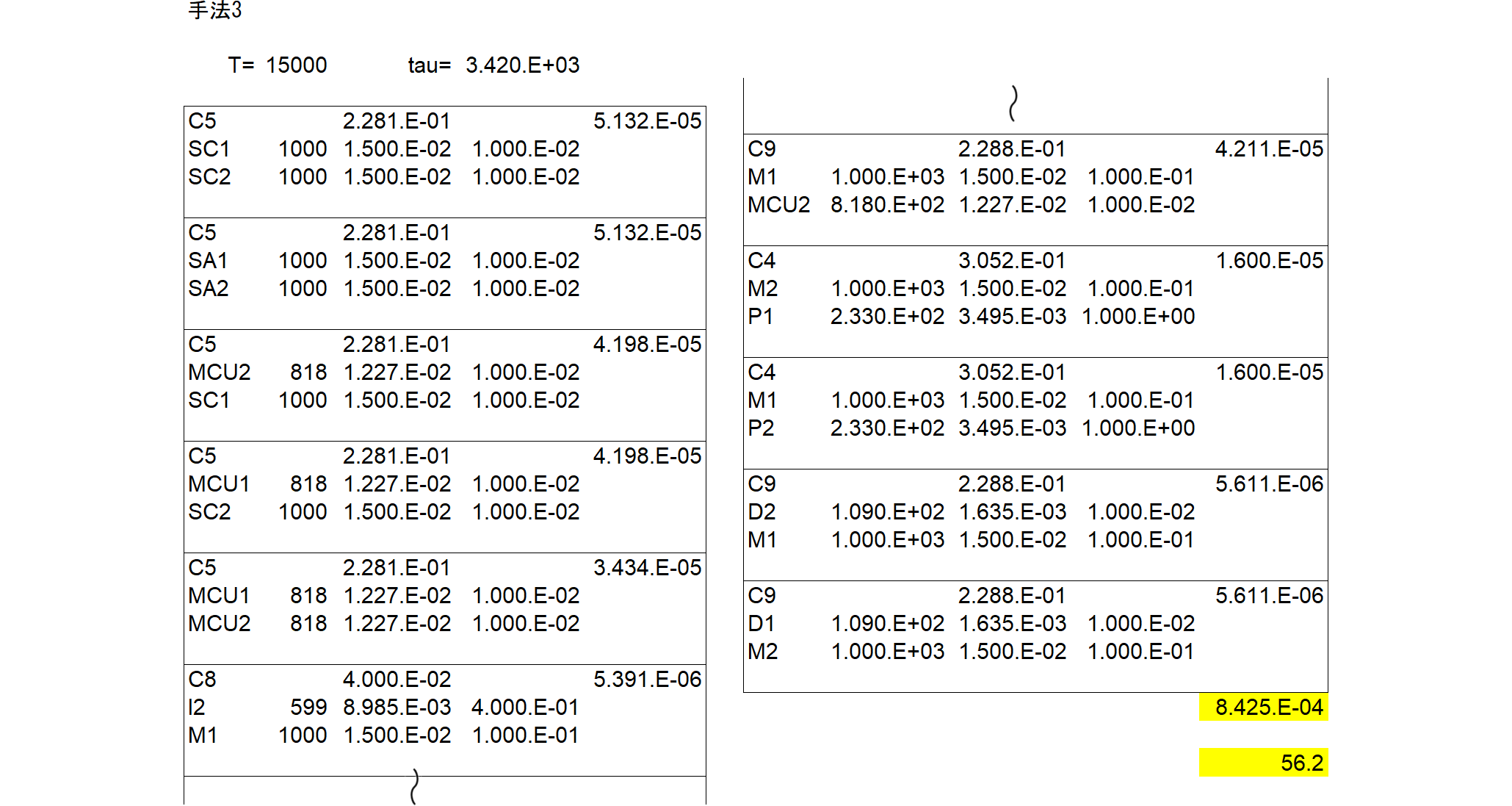
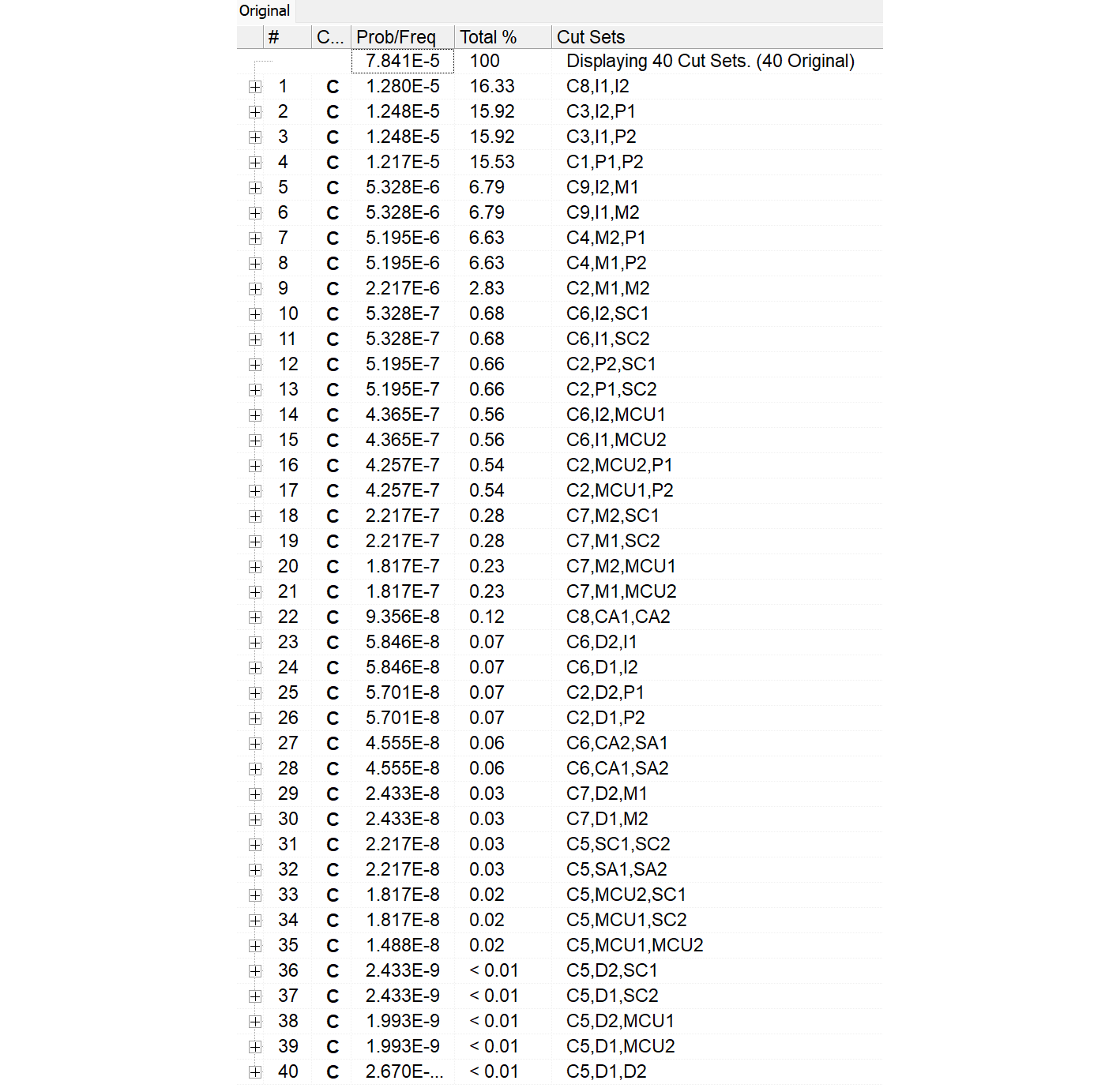
図930.3にSaphireで取得したMCSを示します。予想どおりRFが98%以上であり、DPFは2%未満となりました。
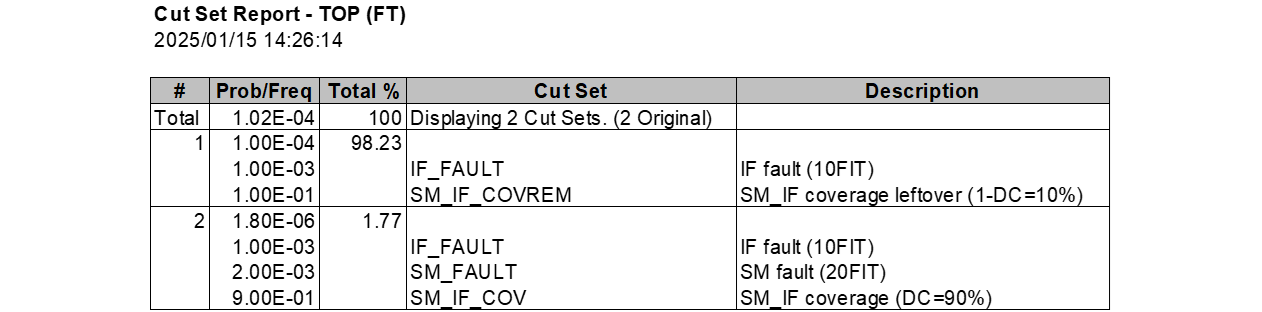
Saphireで生成したcut setの表に対してPMHFの欄を追加し、かつ故障率の項を黄色で塗っています。これによりSPF/RFかDPFかが容易に理解されます。
なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。
$\dagger$ S. Atsushi, "A Framework for Performing Quantitative Fault Tree Analyses for Subsystems with Periodic Repairs," 2021 Annual Reliability and Maintainability Symposium (RAMS), Orlando, FL, USA, 2021, pp. 1-6.