|
17 |
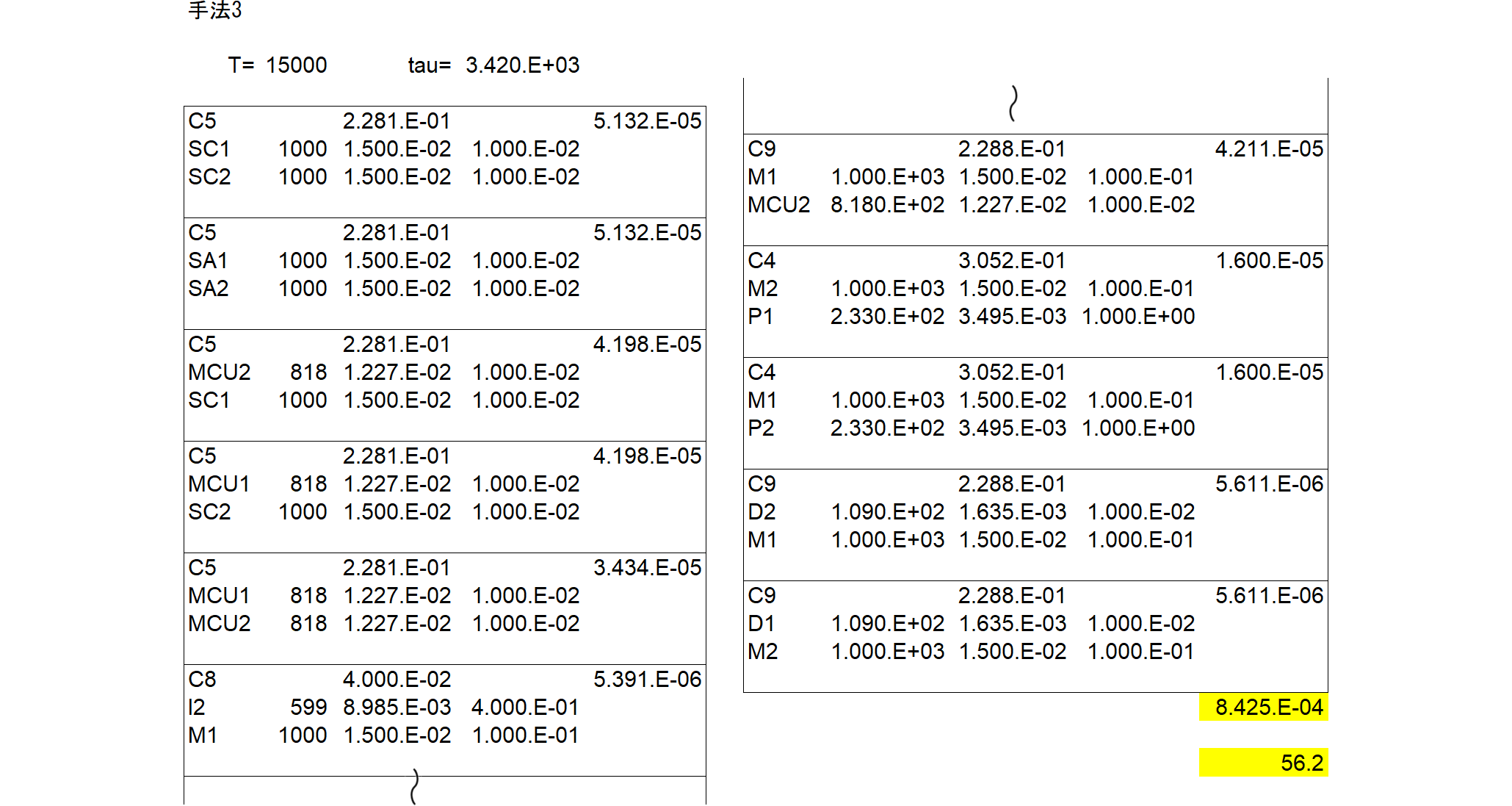
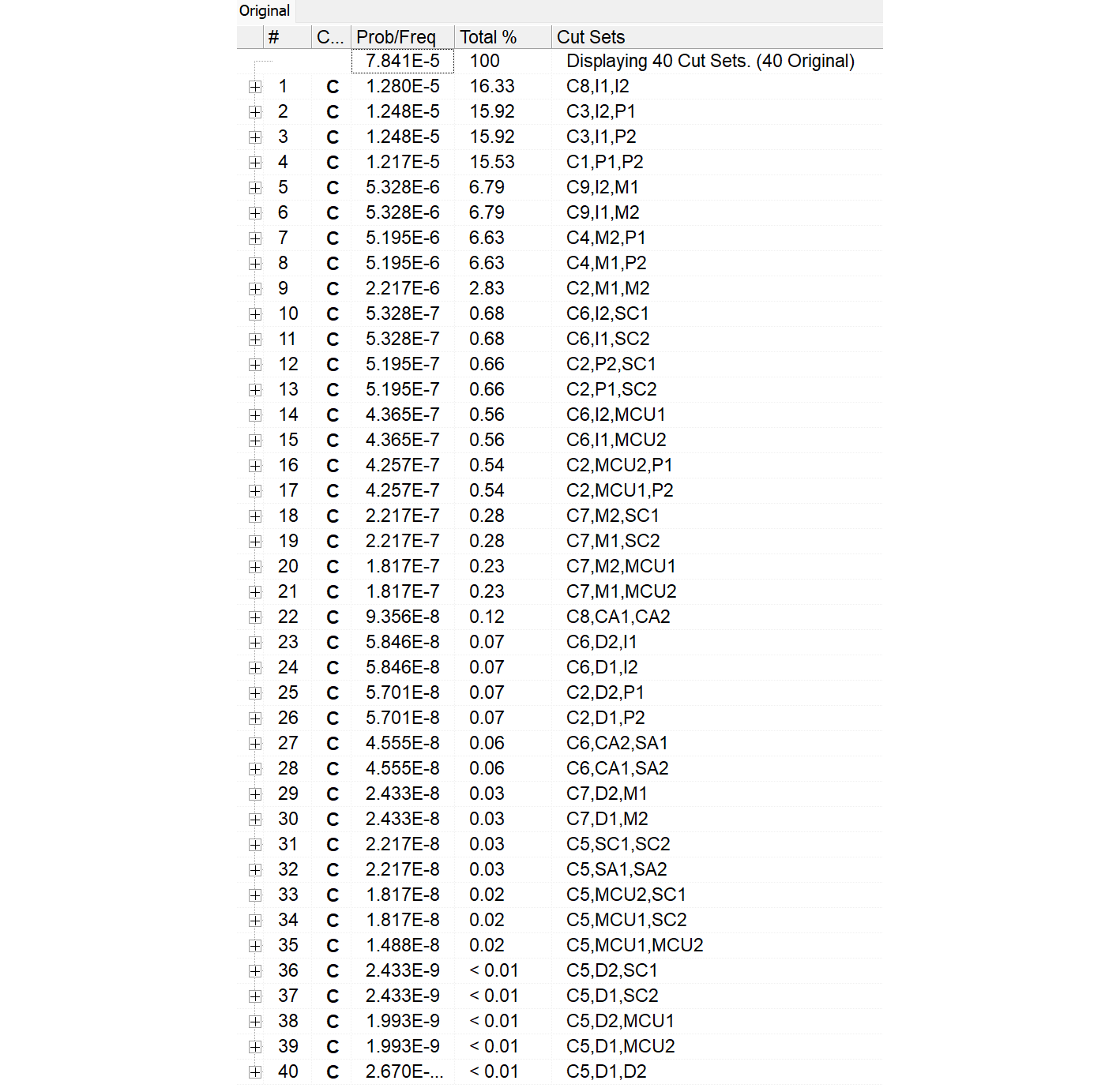
Fault treeの自動生成 (20) |
 |
前稿のExcelの整形マクロはChatGPTにより作成して貰ったものですが、備忘のため貼り付けておきます。
Option Explicit
Sub SampleMacro_Final()
Dim ws As Worksheet
Set ws = ActiveSheet ' カレントシート
'----------------------------------------------------------------------
' (A) まず、B列削除「前」のシートで C列(5行目以降)の最終行を求める
' ここをレコードの最終行とする。
'----------------------------------------------------------------------
Dim lastRow As Long
With ws
lastRow = .Cells(.Rows.Count, "C").End(xlUp).Row
End With
If lastRow < 5 Then
MsgBox "C列の5行目以降にデータがありません。処理を中断します。"
Exit Sub
End If
'----------------------------------------------------------------------
' (1) A6:A(lastRow) を数値化
'----------------------------------------------------------------------
With ws.Range("A6:A" & lastRow)
.NumberFormat = "General"
.Value = .Value
End With
'----------------------------------------------------------------------
' (2) B列を削除
'----------------------------------------------------------------------
ws.Columns("B").Delete
'----------------------------------------------------------------------
' (3) B5:B(lastRow) → 旧C列 の内容を数値化
'----------------------------------------------------------------------
With ws.Range("B5:B" & lastRow)
.NumberFormat = "General"
.Value = .Value
End With
'----------------------------------------------------------------------
' (4) C5:C(lastRow) → 旧D列 の内容を数値化
'----------------------------------------------------------------------
With ws.Range("C5:C" & lastRow)
.NumberFormat = "General"
.Value = .Value
End With
'----------------------------------------------------------------------
' (5) グリッド線のチェックを外す
'----------------------------------------------------------------------
ActiveWindow.DisplayGridlines = False
'----------------------------------------------------------------------
' (6) A4:F4 に罫線 & グレー15% & 中央揃え ほか見出し設定
' - ボールド解除(.Font.Bold = False)
' - B4セルを"Prob" に
' - F4セルに「PMHF」+改行+「[FIT]」
'----------------------------------------------------------------------
With ws.Range("A4:F4")
.Borders.LineStyle = xlContinuous
.Borders.Weight = xlThin
.Borders(xlInsideVertical).LineStyle = xlContinuous
.Borders(xlInsideVertical).Weight = xlThin
.Borders(xlInsideHorizontal).LineStyle = xlContinuous
.Borders(xlInsideHorizontal).Weight = xlThin
.Interior.ColorIndex = 15
.HorizontalAlignment = xlCenter ' 横方向を中央揃え
.VerticalAlignment = xlVAlignCenter ' 縦方向を中央揃え
.Font.Bold = False ' ★ボールドを外す
End With
' ★ B4セルを"Prob"に
ws.Range("B4").Value = "Prob"
' ★ F4セルは改行入りで"PMHF\n[FIT]"
ws.Range("F4").Value = "PMHF" & Chr(10) & "[FIT]"
ws.Range("F4").WrapText = True
'----------------------------------------------------------------------
' (7) A5:F5 を罫線(背景は標準)、揃えはあとでまとめる
'----------------------------------------------------------------------
With ws.Range("A5:F5")
.Borders.LineStyle = xlContinuous
.Borders.Weight = xlThin
.Borders(xlInsideVertical).LineStyle = xlContinuous
.Borders(xlInsideVertical).Weight = xlThin
.Borders(xlInsideHorizontal).LineStyle = xlContinuous
.Borders(xlInsideHorizontal).Weight = xlThin
End With
'----------------------------------------------------------------------
' A列が "total" or 数値 → F列に =B列/1E4*1E9 (小数点1桁表示)
' 対象は 行5~lastRow
'----------------------------------------------------------------------
Dim r As Long
Dim valA As Variant
For r = 5 To lastRow
valA = ws.Range("A" & r).Value
If LCase(valA) = "total" Or (IsNumeric(valA) And Not IsEmpty(valA)) Then
ws.Range("F" & r).Formula = "=B" & r & "/1E4*1E9"
ws.Range("F" & r).NumberFormat = "0.0"
End If
Next r
'----------------------------------------------------------------------
' (8)~(10) グループごとに "外枠のみ" 罫線 → 行6~lastRow
'----------------------------------------------------------------------
Dim i As Long, j As Long
Dim dataA As Variant, dataD As Variant
Dim foundRow As Long
i = 6
Do While i <= lastRow
dataA = ws.Range("A" & i).Value
dataD = ws.Range("D" & i).Value ' 旧E列→新D列
' 終了条件: AもDも空 or i>lastRow
If (IsEmpty(dataA) Or dataA = "") And (IsEmpty(dataD) Or dataD = "") Then
Exit Do
End If
foundRow = 0
For j = i + 1 To lastRow + 1
If j > lastRow Then
foundRow = lastRow + 1
Exit For
End If
Dim tmpA As Variant, tmpD As Variant
tmpA = ws.Range("A" & j).Value
tmpD = ws.Range("D" & j).Value
If (IsEmpty(tmpA) Or tmpA = "") And (IsEmpty(tmpD) Or tmpD = "") Then
foundRow = j
Exit For
End If
If (IsNumeric(tmpA) And Not IsEmpty(tmpA)) Or (IsEmpty(tmpD) Or tmpD = "") Then
foundRow = j
Exit For
End If
Next j
If foundRow = 0 Then
Exit Do
End If
' グループ外枠のみ罫線
Call SetOuterBorders(ws.Range(ws.Cells(i, "A"), ws.Cells(foundRow - 1, "F")))
i = foundRow
Loop
'----------------------------------------------------------------------
' (11)~(15) 相当: A6:F(lastRow) に最終的な罫線(外枠+縦罫線)
'----------------------------------------------------------------------
Call SetOuterBorders(ws.Range("A6:F" & lastRow))
Call SetInsideVerticalBorders(ws.Range("A6:F" & lastRow))
'----------------------------------------------------------------------
' D1結合対策(任意)
'----------------------------------------------------------------------
ws.Range("D1").MergeArea.ClearContents
With ws.Range("A1:E1")
.Merge
.HorizontalAlignment = xlLeft
End With
'----------------------------------------------------------------------
' E列の色付け
'----------------------------------------------------------------------
Dim valE As Variant
Dim strE As String
For r = 5 To lastRow
valA = ws.Range("A" & r).Value
Dim strA As String
strA = Replace(Replace(Replace(CStr(valA), vbCr, ""), vbLf, ""), " ", "")
strA = Trim(strA)
If LCase(strA) = "total" Or (IsNumeric(strA) And strA <> "") Then
ws.Range("E" & r).Interior.ColorIndex = xlNone
Else
valE = ws.Range("E" & r).Value
strE = Replace(Replace(Replace(CStr(valE), vbCr, ""), vbLf, ""), " ", "")
strE = Replace(strE, Chr(160), "")
strE = Trim(strE)
Dim pGen As Long
pGen = InStr(1, strE, "; GEN=", vbTextCompare)
If pGen = 0 Then
pGen = InStr(1, strE, ";GEN=", vbTextCompare)
End If
If pGen > 0 Then
strE = Trim(Left(strE, pGen - 1))
End If
Dim chkE As String
chkE = LCase(strE)
If Right(chkE, 1) = ")" Then
chkE = Left(chkE, Len(chkE) - 1)
End If
If chkE = "" Then
ws.Range("E" & r).Interior.ColorIndex = xlNone
ElseIf Right(chkE, 3) = "fit" Then
ws.Range("E" & r).Interior.Color = RGB(249, 241, 227)
ElseIf Right(chkE, 1) = "%" Then
ws.Range("E" & r).Interior.ColorIndex = xlNone
Else
ws.Range("E" & r).Interior.ColorIndex = 45
End If
End If
Next r
'----------------------------------------------------------------------
' ★ もともとD5にあった括弧を削除(最終的にはD4になる)
'----------------------------------------------------------------------
Dim tmpStr As String, p As Long
tmpStr = ws.Range("D5").Value
p = InStr(tmpStr, "(")
If p > 0 Then
tmpStr = Trim(Left(tmpStr, p - 1))
ws.Range("D5").Value = tmpStr
End If
'----------------------------------------------------------------------
' 行2を削除 → D5 が D4 に繰り上がる
'----------------------------------------------------------------------
ws.Rows(2).Delete
lastRow = lastRow - 1
'----------------------------------------------------------------------
' 列オートフィット & 横位置調整
' 見出し行(A4:F4) → 実際は A3:F3 になる
' データ行(A5:F...) → 実際は A4:F...
'----------------------------------------------------------------------
ws.Range("A3:F" & lastRow).Columns.AutoFit
With ws.Range("A4:A" & lastRow): .HorizontalAlignment = xlRight: End With
With ws.Range("B4:B" & lastRow): .HorizontalAlignment = xlRight: End With
With ws.Range("C4:C" & lastRow): .HorizontalAlignment = xlRight: End With
With ws.Range("D4:D" & lastRow): .HorizontalAlignment = xlLeft: End With
With ws.Range("E4:E" & lastRow): .HorizontalAlignment = xlLeft: End With
With ws.Range("F4:F" & lastRow): .HorizontalAlignment = xlRight: End With
MsgBox "処理が完了しました。最終行は " & lastRow
End Sub
'------------------------------------------------------------------------------
' 外枠だけ罫線を付ける
'------------------------------------------------------------------------------
Private Sub SetOuterBorders(rng As Range)
With rng
With .Borders(xlEdgeLeft)
.LineStyle = xlContinuous
.Weight = xlThin
End With
With .Borders(xlEdgeTop)
.LineStyle = xlContinuous
.Weight = xlThin
End With
With .Borders(xlEdgeRight)
.LineStyle = xlContinuous
.Weight = xlThin
End With
With .Borders(xlEdgeBottom)
.LineStyle = xlContinuous
.Weight = xlThin
End With
End With
End Sub
'------------------------------------------------------------------------------
' 縦の内側線だけ
'------------------------------------------------------------------------------
Private Sub SetInsideVerticalBorders(rng As Range)
With rng.Borders(xlInsideVertical)
.LineStyle = xlContinuous
.Weight = xlThin
End With
End Sub
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。
なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。