|
29 |
Fault treeの自動生成 (22) |
 |
一連のスレッドですがタイトルは以前の記事から引き継いでいます。
それではEGASアーキテクチャのブロック図を図939.1に示すので、MARDを提供して下さい。
$$\img[-1.35em]{/images/withinseminar.png}$$
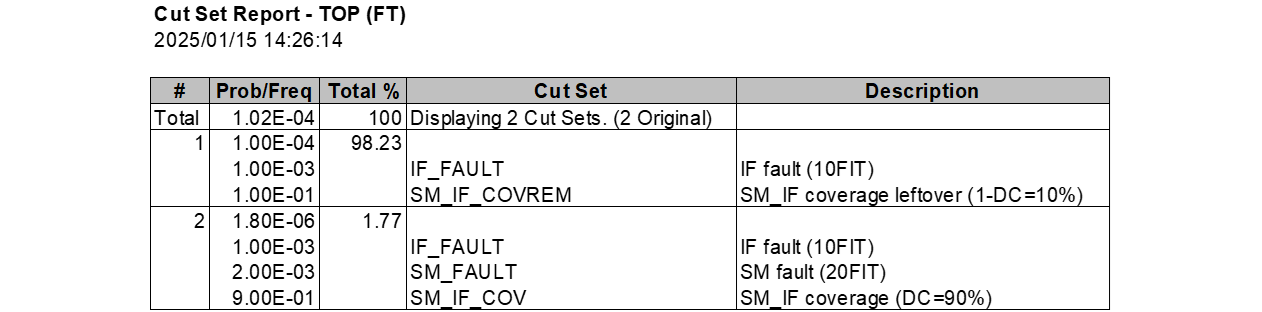
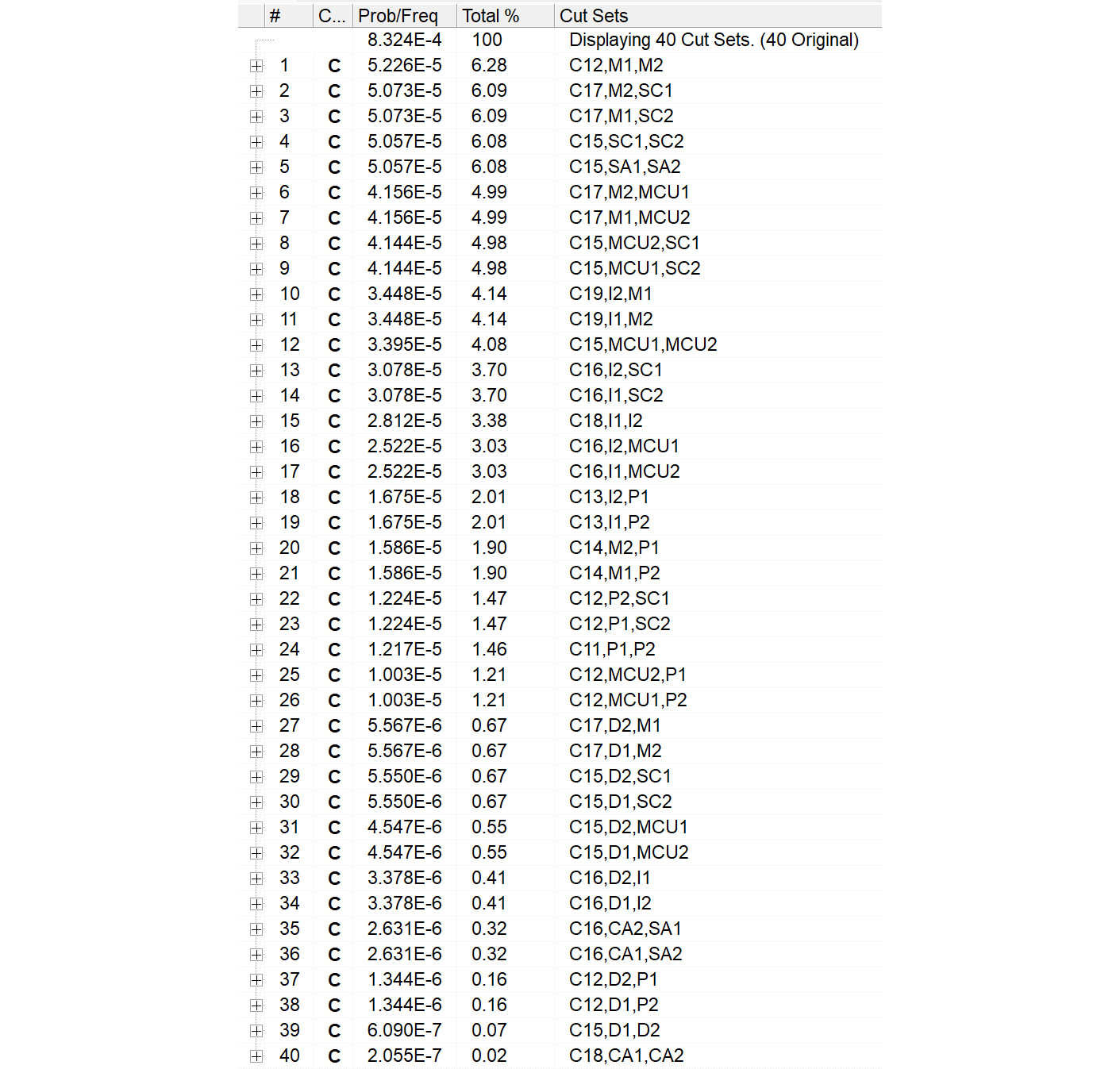
図939.1を読み取ったChatGPTの生成したMARDファイルを以下に示します。
TEST.BED
*Saphire 8.2.9
TEST =
* Name , Descriptions , Project
APS_SENSOR , APS sensor (1FIT) , TEST
TPS_SENSOR , TPS sensor (1FIT) , TEST
FCAN_LINE , FCAN line (10FIT) , TEST
MAIN_MCU , Main MCU (200FIT) , TEST
MOTOR_DRV , Motor driver (10FIT) , TEST
DRIVER_DIAG , Driver DIAG (1FIT) , TEST
SUB_MCU , Sub MCU (150FIT) , TEST
RELAY_DRV , Relay driver (10FIT) , TEST
COV_REM , SM leftover (1-DC=10%) , TEST
COV_90 , SM coverage (DC=90%) , TEST
TEST.BEI
*Saphire 8.2.9
TEST =
* Name ,FdT,UdC,UdT,UdValue, Prob, Lambda, Tau, Mission, Init,PF,UdValue2,Calc. Prob,Freq,Analysis Type,Phase Type,Project
APS_SENSOR ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
TPS_SENSOR ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
FCAN_LINE ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
MAIN_MCU ,3, , , , ,2.0E-007, ,1.0E+004, , , ,2.0E-003, ,RANDOM,CD,TEST
MOTOR_DRV ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
DRIVER_DIAG ,3, , , , ,1.0E-009, ,1.0E+004, , , ,1.0E-005, ,RANDOM,CD,TEST
SUB_MCU ,3, , , , ,1.5E-007, ,1.0E+004, , , ,1.5E-003, ,RANDOM,CD,TEST
RELAY_DRV ,3, , , , ,1.0E-008, ,1.0E+004, , , ,1.0E-004, ,RANDOM,CD,TEST
COV_REM ,1, , , ,1.0E-001, , , , , , ,1.0E-001, ,RANDOM,CD,TEST
COV_90 ,1, , , ,9.0E-001, , , , , , ,9.0E-001, ,RANDOM,CD,TEST
TEST.FTD
TEST =
* Name , Description, SubTree, Alternate, Project
TOP , TEST , , , TEST
TEST.FTL
TEST, TOP =
TOP AND IF_FAIL SM_FAIL
IF_FAIL OR APS_SENSOR TPS_SENSOR FCAN_LINE MAIN_MCU MOTOR_DRV
SM_FAIL OR COV_REM SM_PATH
SM_PATH AND COV_90 SM_EXPAND
SM_EXPAND OR DETECT_FAIL CTRL_FAIL
DETECT_FAIL AND APS_SENSOR TPS_SENSOR DRIVER_DIAG SUB_MCU
CTRL_FAIL OR MAIN_MCU RELAY_DRV
TEST.GTD
TEST=
* Name , Description, Project
TOP , TEST , ,TEST
IF_FAIL , IF fail , ,TEST
SM_FAIL , SM fail , ,TEST
SM_PATH , coverage path , ,TEST
SM_EXPAND , SM expand , ,TEST
DETECT_FAIL , detection fail , ,TEST
CTRL_FAIL , control fail , ,TEST
図939.2にこれらのMARDをSpahireにロードし生成したFTを示します。
$$\img[-1.35em]{/images/withinseminar.png}$$
なお、本稿はRAMS 2026に投稿予定のため一部を秘匿していますが、論文公開後の2026年2月頃に開示予定です。