引き続き(b)~(d)の平均PUD計算
前稿において、
(a) OPR$\rightarrow$SPF
が求められましたが、結果として$K_\text{IF,RF}$に対して$\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}$を代入した形となりました。よって、
(b) LAT2$\rightarrow$SPF
(c) LAT2$\rightarrow$DPF
(d) LAT1$\rightarrow$DPF
残りの(b), (c), (d)を同様に求めます。過去記事のPMHF結果式(373.1)において、上記を代入し、
$$
\begin{eqnarray}
M_\text{PMHF}&=&\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\right)\lambda_\text{IF}+\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\color{red}{K_\text{IF,det}}\alpha+2\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta\\
&=&\img[-1.35em]{/images/withinseminar.png}\\
\end{eqnarray}\tag{385.1}
$$
ただし、
$$
\begin{cases}
\begin{eqnarray}
\alpha&:=&\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}T_\text{mpfdi}],\\
\beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}T_\text{mpfdi}],\\
K_{\mathrm{MPF}}&:=&K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}}
\end{eqnarray}
\end{cases}
$$
となります。
EOTTIの詳細なタイミング
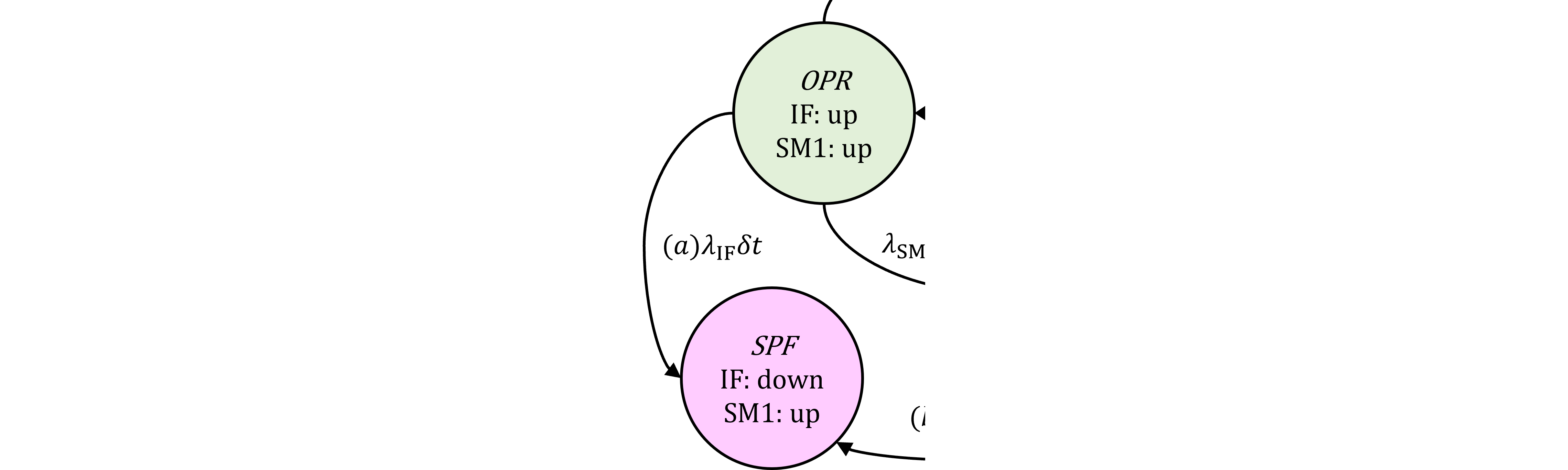
以上の議論は、EOTTI時間間隔とMPFDI時間間隔の比に依存すると単純化してきましたが、実際にはIFのフォールトは図385.1のように生起します。
 図385.1 フォールト発生から修理まで
図385.1 フォールト発生から修理まで
詳細に見れば、フォールト発生から修理まではSM1によりVSG抑止されていますが、この時間内にSM1にフォールトが発生するとDPFとなります。今回の議論においては、EOTTIでカバーされる時間内では
即時修理される前提でhit率を計算したため、そこに若干の齟齬が出るはずです。
良く考えると、IFの1点フォールトでレイテントとなり、定期検査で修理されて正常に戻る図385.1の動作は、以前のMPF detectedがレイテントであった頃と変わりません。IFでのフォールト生起から検査・修理までの時間間隔においてSM1にフォールトが発生するとDPFとなるためです。従って、この条件でPMHFを求めると、元に戻って(LFMとは矛盾を起こすようにはなるものの)求められたPMHF式に、EOTTIの効果を入れれば良いことになります。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です。
 前のブログ
次のブログ
前のブログ
次のブログ