OPR⇒SPFの平均PUDの計算

従来はMPF detectedはnon faultyでしたが、今回EOTTIの導入に伴い、SM1の時間制約としてのEOTTI後に、VSG抑止の時間切れとなることからSPFとするように変更しました。従って、MPF detectedといえどもSPF計算に関係してきます。 前稿#369を参照し、OPRからSPFへの平均PUD(66.13)を計算します。

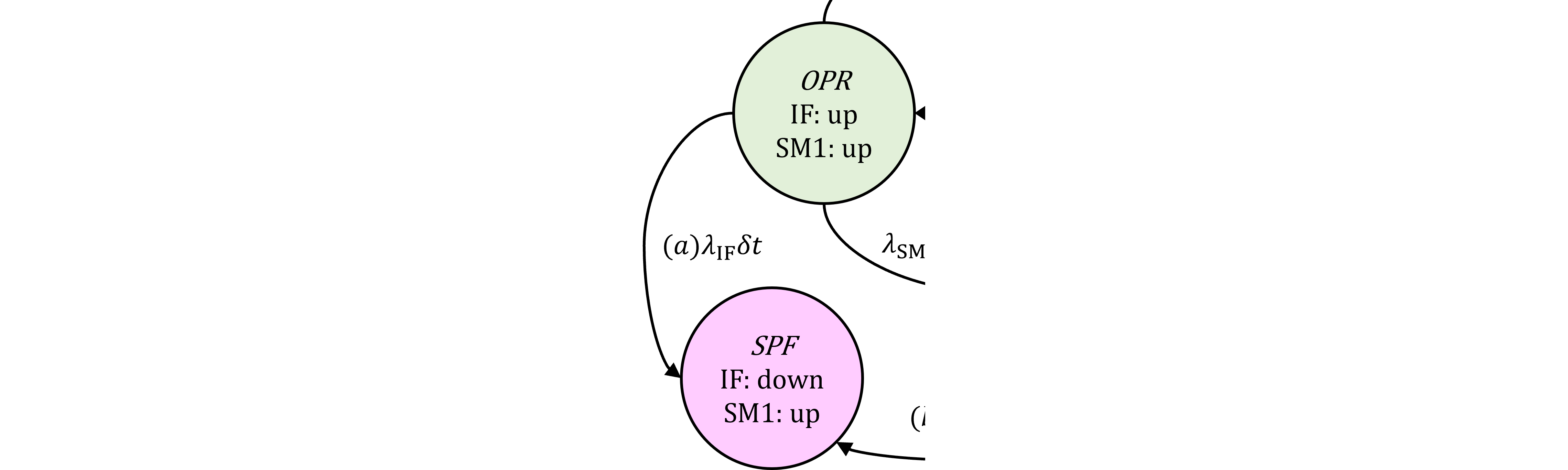
OPRからSPFへの平均PUDは、 $$ \overline{q_{\mathrm{SPF(a),IFU}}}=\frac{1}{T_\text{lifetime}}\Pr\{\mathrm{SPF\ via\ (a)\ at\ }T_\text{lifetime}\}\tag{384.1} $$ ここで、表368.1より、IF non preventableのupは(2)及び(4)のうちEOTTIでカバーされない分=miss分=(383.1)、の2排他条件であるため、 $$ \begin{eqnarray} (384.1)&=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\left(\mathrm{OPR_\overline{prev}\ at\ }t\cup\mathrm{OPR_\text{prev}\ at\ }t\cap miss\right)\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ & &+\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\left(\mathrm{OPR_\overline{prev}\ at\ }t\cap miss\right)\cap\mathrm{IF\ down\ in\ }(t, t+dt]\}\\ &=&\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\overline{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\}\\ & &+\frac{\Pr\{miss\}}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\text{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\text{prev}\ at\ }t\}\\ \end{eqnarray} \tag{384.2} $$ 前稿#369の(369.5)より、 $$ \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_\overline{prev}\ at\ }t\}\Pr\{\mathrm{OPR_\overline{prev}\ at\ }t\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}(1-K_\mathrm{IF,RF})R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.3} $$ さらに、 $$ \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\Pr\{\mathrm{IF\ down\ in\ }(t, t+dt]\ |\ \mathrm{OPR_{prev}\ at\ }t\}\Pr\{\mathrm{OPR_{prev}\ at\ }t\}\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}K_\mathrm{IF,RF}R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.4} $$ は明らかであるから、これらを(384.2)に代入して、 $$ \require{cancel} (384.2)=\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left[(1-\bcancel{K_\text{IF,RF}})+K_\text{IF,RF}\left(\bcancel{1}-\frac{T_\text{eotti}}{T_\text{mpfdi}}\right)\right]R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt\\ =\frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\text{IF,RF}\right)R_\mathrm{IF}(t)A_\mathrm{SM}(t)\lambda_\mathrm{IF}dt \tag{384.5} $$ よって、(103.6)の結果を用い、$\tau=T_\text{mpfdi}$であるから、 $$ \begin{eqnarray} (384.5)&\approx&\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\right)\lambda_\mathrm{IF}-\left(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\right)\alpha\\ &=&\img[-1.35em]{/images/withinseminar.png}\\ & &\text{ただし、} \alpha:=\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}\left[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}T_\text{mpfdi}\right] \end{eqnarray} \tag{384.6} $$

MPFDIに対してEOTTI分だけSM1のカバレージが減少すると解釈すると、SM1のEOTTIの制約に対して理屈に合っています。

なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です。

前のブログ 次のブログ