|
18 |
新方式によるPUAの導出 (3) |
さて、微小時間間隔$(t, t+dt)$における不検出部分の微小確率$q_\text{undet}(t)$は、 $$ q_\text{undet}(t)=\Pr\{\text{undetected}\cap\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ =\Pr\{\text{undetected}\hspace{1pt}|\hspace{1pt}\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ \cdot\Pr\{\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ =(1-K_\text{MPF})\cdot\Pr\{\text{failed in }(t, t+dt)\hspace{1pt}|\hspace{1pt}\text{up at }t\}\cdot\Pr\{\text{up at }t\}\\ =(1-K_\text{MPF})\lambda dt R(t)=(1-K_\text{MPF})f(t)dt\tag{756.1} $$ でした。不検出部分は修理の影響を全く受けないため、$Q(t)$は $$ Q_\text{undet}(t)=\int_0^t q_\text{undet}(s)ds=(1-K_\text{MPF})\int_0^tf(s)ds=(1-K_\text{MPF})F(t)\tag{756.2} $$ 他方、検出部分の微小確率$q_\text{det}(t)$は $$ q_\text{det}(t)=\Pr\{\text{detected}\cap\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ =\Pr\{\text{detected}\hspace{1pt}|\hspace{1pt}\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ \cdot\Pr\{\text{failed in }(t, t+dt)\cap\text{up at }t\}\\ =K_\text{MPF}\cdot\Pr\{\text{failed in }(t, t+dt)\hspace{1pt}|\hspace{1pt}\text{up at }t\}\cdot\Pr\{\text{up at }t\}\\ =K_\text{MPF}\lambda dt R(t)=K_\text{MPF}f(t)dt\tag{756.3} $$ この微小確率は累積せずに区間毎に修理され、最後の区間のみ累積されるため、$Q(t)$は $$ \require{cancel} Q_\text{det}(t)=\int_0^t q_\text{det}(s)ds=K_\text{MPF}\int_{n\tau}^t f(s)ds=K_\text{MPF}\left[F(t)-F(n\tau)\right]\\ =K_\text{MPF}\left((\bcancel{1}-e^{-\lambda t})-(\bcancel{1}-e^{-\lambda n\tau})\right)=K_\text{MPF}e^{-\lambda n\tau}\left(1-e^{-\lambda(t-n\tau)}\right)\\ =K_\text{MPF}R(n\tau)F(u) ,\ \ s.t.\ n=\lfloor \frac{t}{\tau}\rfloor,\ u=t\bmod\tau\tag{756.4} $$ 式(756.2)及び (756.4)を加えて、 $$ Q(t)=(1-K_\text{MPF})F(t)+K_\text{MPF}R(n\tau)F(u) ,\ \ s.t.\ n=\lfloor \frac{t}{\tau}\rfloor,\ u=t\bmod\tau\tag{756.5} $$
図756.1に、 $$ \begin{eqnarray} \begin{cases} Q_1(t)&=(1-K_\text{MPF})F(t)+K_\text{MPF}F(u)\\ Q_2(t)&=(1-K_\text{MPF})F(t)+K_\text{MPF}R(n\tau)F(u) ,\ \ s.t.\ n=\lfloor t/\tau\rfloor,\ u=t\bmod\tau\tag{756.6} \end{cases} \end{eqnarray} $$ のグラフを示します。青が$Q_1(t)$、赤が$Q_2(t)$です。
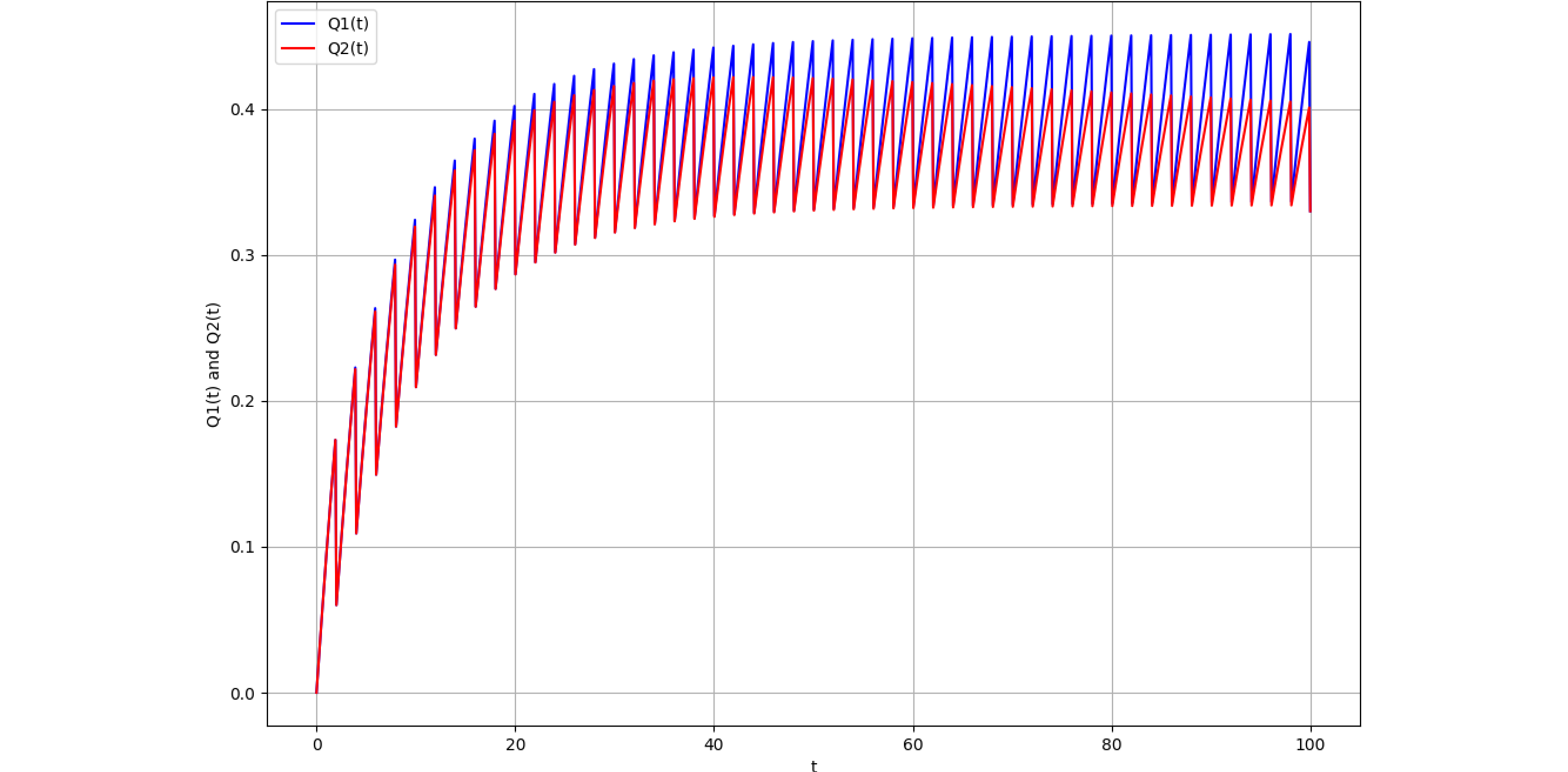
本来なら$Q_2(t)$を使用すべきですが、$Q_1(t)$を近似式として使用します。
注意:
本記事は上記のこのマーカーの箇所が誤りのようです。上記は修理可能部分の不信頼度は累積されないとして計算しましたが、実際には不信頼度は累積され、区間の最後で修理されます。従って、本来不信頼度の累積は高い不稼働度になるところが、本計算ではより低く見積もることになります。
なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。
