以下の記事中、ピンクは誤り、グリーンは正解を意味しています。

過去記事ではまずPUDを導出し、途中の検出分が全て修理される前提で、最終の検出かつ未修理分のみを不検出に加えてPUAを導出しました。

一方、過去記事において不稼働度(Point Unavailability; PUA)を新方式$\dagger$で求めました。ところが導出の際に式の誤りがあったため再度同じ方法で不稼働度(PUA)を求めてみます。

SMのフォールトが生起したとき、それがレイテントフォールトとなるかならないかは2nd SMの故障検出率で決定されます。これを$K_\text{MPF}$とすると、 $$ K_\text{MPF}=\Pr\{\text{detected }|\text{ failed at }t\}\tag{758.1} $$ ここでは式(758.1)に基づいてPUAを導出します。これは、修理が完全に確率的に行われることを意味し、検出されるされないは故障の原因によらずにSMの能力のみに依存することになります。これは従来の仮定を根本から変更するものであるため、本稿では「新方式」としています。

不稼働度$Q(t)$の一般式

稼働度(Point Availability; PA)の公式から不稼働度は以下のように表せます。 $$ \begin{eqnarray} Q_n(t)&=&F(t)-\int_0^{T_\text{lifetime}}m(x)R(t-x)dx\\ &=&F(t)-\sum_{i=1}^nM(i\tau)R(t-i\tau)\tag{758.2} \end{eqnarray} $$ 定期修理であるため、$\tau_i=i\tau,\ i=1,2,...$が修理時点であり、$M(i\tau)$は修理時点$i\tau$における修理率です。不稼働度はフォールトが起きて累積する検出率に応じた一部の故障が修理され、かつ現在まで生き残っている分を引いたものとなります。

さて、修理時点$i\tau$における修理率$M(i\tau)$はその検査区間内での不信頼度の増加分に故障検出率である(758.1)の$K_\text{MPF}$をかけたものとなることから、 $$ \begin{eqnarray} M(i\tau)&=&K_\text{MPF}\int_{i-1}^iq(x)dx\\ &=&\img[-1.35em]{/images/withinseminar.png} \tag{758.3} \end{eqnarray} $$ なぜその検査区間内かといえば、その前までの故障は全て検査され、不検出分は全てレイテントフォールトとなり不信頼度に加えられるからです。

従って、(758.2), (758.3)より、 $$ Q_n(t)=F(t)-\img[-1.35em]{/images/withinseminar.png}\ n=\lfloor t/\tau\rfloor\ge1\tag{758.4} $$ しかしながら、PUAは求めるべき関数が右辺にあるため陽には求められず、数値計算することになります。図758.1は$\lambda$=0.001, $\tau$=100のときのグラフです。

• $F(t)$ --- 紫
• $Q_\text{exact}(t)$ --- 赤
• $Q_\text{approx}(t)=(1-K)F(t)+KF(u)$ --- 青
• $Q_\text{approx}(t)$のベースライン$(1-K)F(t)$ --- 緑

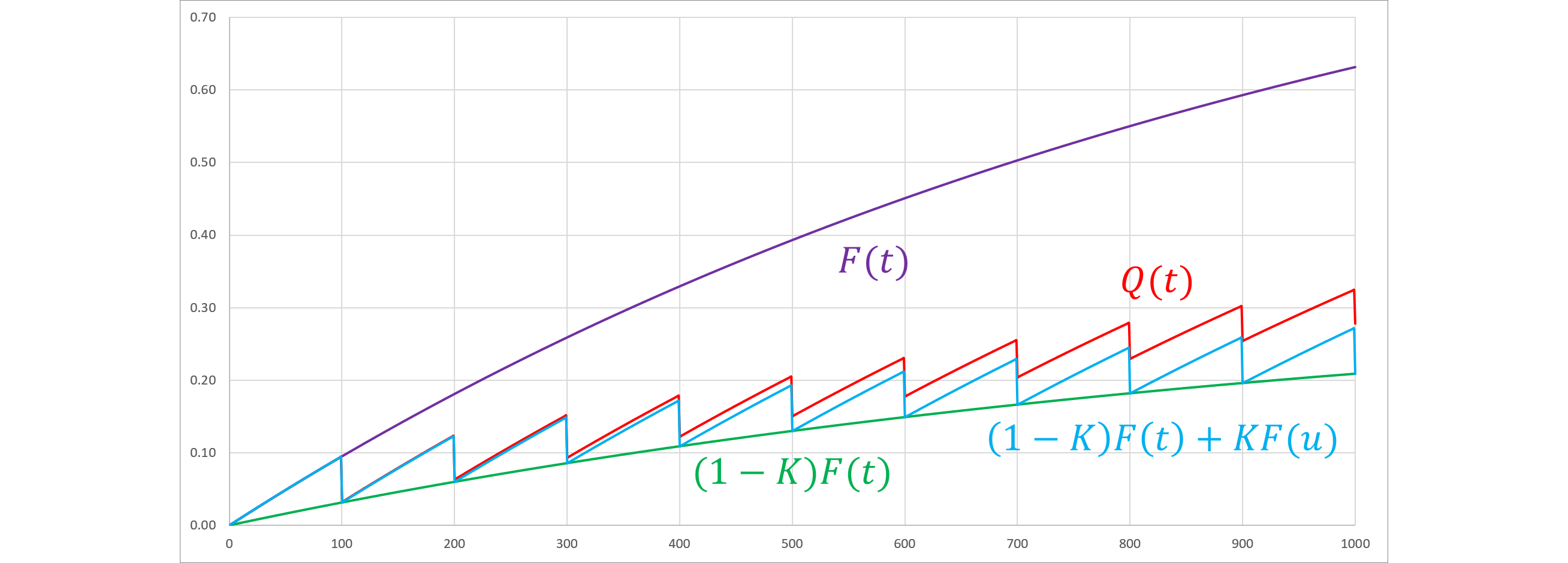
従来論文ではPUAとして青の$Q_\text{approx}(t)=(1-K)F(t)+KF(u)$を用いていますが、本来は毎回の修理量は徐々に減少していき、不信頼度が増大するため赤の$Q_\text{exact}(t)$のように上振れとなります。

今までの記事は区間修理量一定という、厳密な議論に立てば正しくない仮定の下にPUA及びPUDを導出してきましたが、正しくは本記事のように区間修理量は漸減するとすべきでした。

なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。

$\dagger$2nd SMのDCである$K_\text{MPF}$を条件付き確率と変更する方式

前のブログ 次のブログ