|
21 |
EOTTIの考え直し (3) |
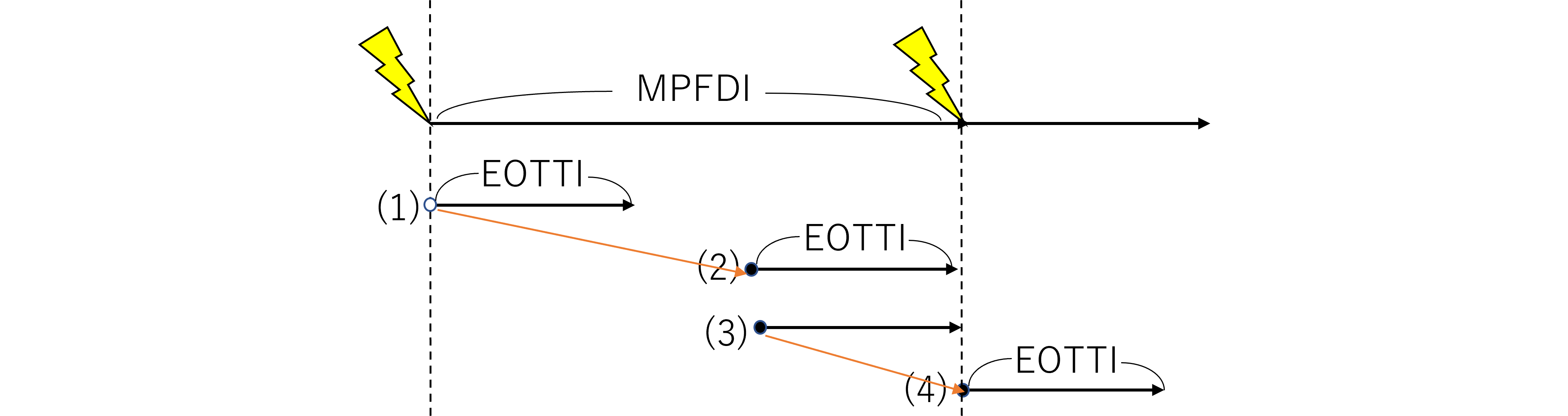
前稿において、ようやくSM1にEOTTI制約がある場合についての$M_\text{PMHF}$が求められたので、今回は以前のブログ記事にならい、非冗長におけるEOTTIの制約を求めます。ただし、MPFDIを定めないとEOTTIが定まらないという制約があるので、MPFDIを100H, 10H, 1Hのように振ってみます。
さて、非冗長であることから(385.1)に$K_\text{IF,det}=1$を代入し、 $$ \begin{eqnarray} M_\text{PMHF}&=&(1-\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF})\lambda_\text{IF}+\frac{T_\text{eotti}}{T_\text{mpfdi}}K_\mathrm{IF,RF}\alpha \end{eqnarray}\tag{386.1} $$ ただし、 $$ \alpha:=\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}T_\text{mpfdi}] $$ となります。よって、EOTTIの最大値は、 $$ \frac{M_\text{PMHF}-\lambda_\text{IF}}{\alpha-\lambda_\text{IF}}\cdot\frac{T_\text{mpfdi}}{K_\text{IF,RF}}\\ =\frac{M_\text{PMHF}-\lambda_\text{IF}}{\frac{1}{2}\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}T_\text{mpfdi}]-\lambda_\text{IF}}\cdot\frac{T_\text{mpfdi}}{K_\text{IF,RF}}\\ =\img[-1.35em]{/images/withinseminar.png} \tag{386.2} $$ で求められます。
規格に記述されている数値を入れてみたところ、矛盾が起きました。その理由は規格が誤ったPMHF方程式に基づいているためのようです。従ってEOTTIの最大値を具体的な数値について議論することは断念しました。
なお、本稿はRAMS 2027に投稿予定のため一部を秘匿していますが、論文公開後の2027年2月頃に開示予定です。