|
24 |
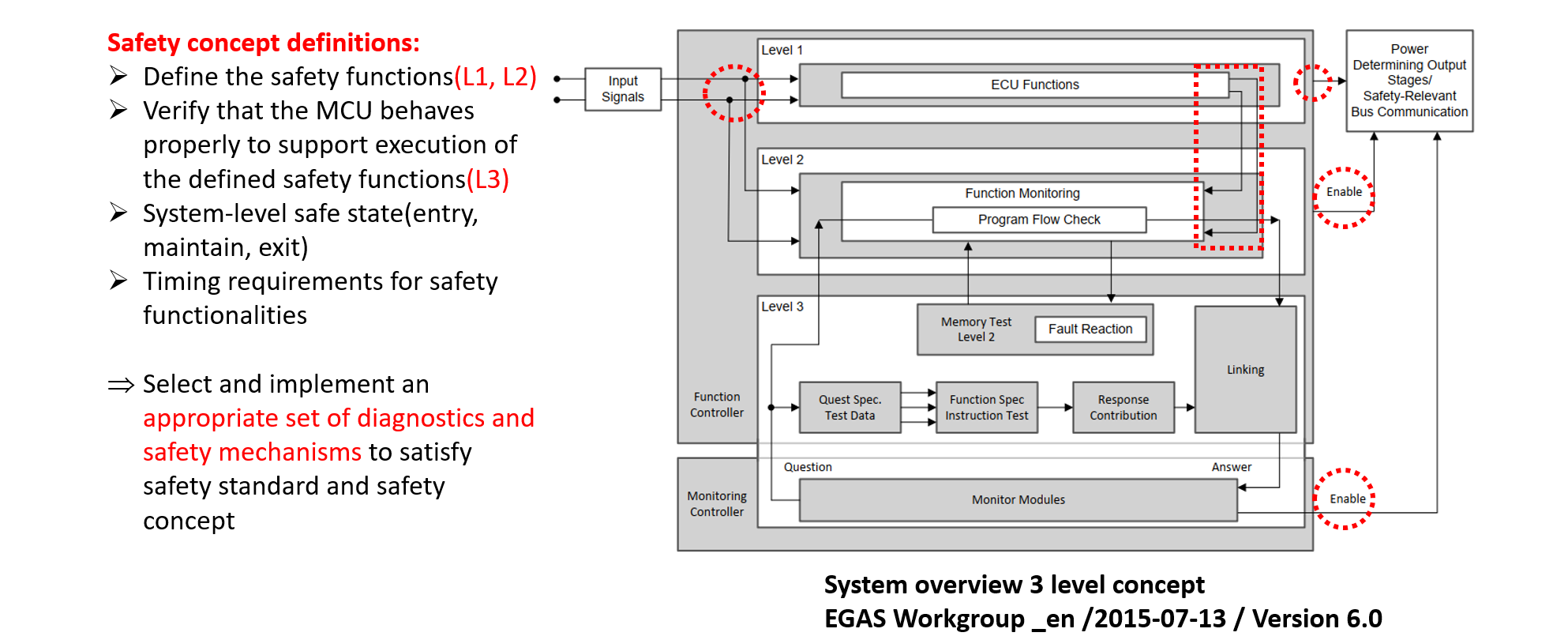
EGASアーキテクチャ (4) |
 |
2エレメントの間のCCF、もしくは3層の間のCCFが起きる可能性は無いか探してください。
ChatGPT:
2エレメント構成や3層構造によって単一点故障への耐性を高めたとしても、CCF (Common Cause Failure: 共通要因故障) の可能性がゼロにはなりません。ISO 26262などの機能安全規格においても、CCFは必ず考慮すべき重要なリスクとして明示されており、メイン系とモニタ系の間、あるいは入力層・制御層・出力層の各層間で同時故障につながる共通要因が潜在していないかどうかを評価・低減するプロセスが必要です。
以下では、(1) 2エレメント間のCCF要因 と (2) 3層間のCCF要因 をそれぞれ整理し、どのように発生しうるかとその対策の考え方を概説します。
1. 2エレメント(メイン系とモニタ系)間のCCF要因
2つの独立した制御経路(エレメント)を用意しても、以下のような“共通要因”が原因で両系統が同時にダウンしたり、誤作動を起こす可能性があります。
1-1. 同一ソフトウェア/ツールチェーンに起因するバグ
- 概要
メイン系・モニタ系ともに、同一ソースコード(同一アルゴリズム)や同一コンパイラを使っている場合、共通のソフトウェアバグやコンパイラバグにより、両系統が同時に不正な動作を行う可能性があります。 - 対策
- ソフトウェア多様化: 重要な演算ロジックを別言語や別アルゴリズムで実装(同一バグに陥る確率を下げる)。
- ツールチェーン多様化: 可能な範囲で異なるコンパイラ/リンカを使用し、共通バグを回避する。
- ソフトウェア検証プロセス(静的解析、MISRA適合、単体/結合テスト)の強化。
1-2. ハードウェア/電源まわりの設計不良やノイズ
- 概要
メイン系とモニタ系が同一基板や同一電源回路を共有している場合、電源の瞬断、過電圧、過剰ノイズなどが同時に両系統へ悪影響を与え、同時故障につながる可能性があります。 - 対策
- 電源の物理的/論理的分離(例: メイン系とモニタ系それぞれに独立したレギュレータやフィルタを配置)。
- グラウンド(アース)のパターン分離やノイズフィルタの追加。
- システムレベルでのEMC/EMI試験を十分実施し、外来ノイズやサージに対する保護回路を強化。
1-3. 製造不良や同一ICの“シリコンバグ”
- 概要
メイン系・モニタ系が同一型番/同一シリコンのマイコンを使用している場合、製造段階の欠陥(シリコンバグ)や経年劣化が同じタイミングで顕在化する場合があります。 - 対策
- 異なるベンダーや型番のマイコンを採用して多様化を図る。
- メイン系とモニタ系でステッピング(製造ロット)をずらす。
- シリコンベンダーが公表するエラッタ情報(Errata)を確認し、回避策を適用。
2. 3層(入力・制御・出力)間のCCF要因
3つの階層に分割して冗長化/診断機構を組み込んでも、各層のあいだに生じる共通要因で故障が波及し、同時に多層が機能不全に陥るリスクがあります。
2-1. センサ層(入力層)の共通ハーネス不良や環境要因
- 概要 ペダル位置センサやスロットル位置センサを二重化していても、配線ハーネスの取り回しが同一ルートを経由していると、ショートや断線が同時に起きやすい。また、過酷な環境(高温・高湿・塩害・振動など)が同時に複数のセンサを故障させる可能性もある。
- 対策
- 配線・コネクタのルーティングを分離し、単一点障害で両チャネルを同時に失わない設計。
- 異なる物理センサ(ホール素子式 + ポテンショ式 など)を併用し、共通の故障モードを減らす。
- 防水・防振・防塵などハードウェアの実装クオリティを向上。
2-2. 制御層(マイコン/ソフト)での同時障害
- 概要
制御層(メイン系・モニタ系)はもともと2エレメントに分かれていますが、OSやハードウェアリソースの一部を共有するなど、内部的に共通する部分(電源、クロック、リセット回路、ウォッチドッグなど)がある場合、そこが1箇所壊れただけで両系統ともダウンするリスクがあります。 - 対策
- 重要なクロック源やリセット回路などを2系統分離、あるいはシステムレベルで安全監視する。
- ソフトウェアのコモンモジュール(初期化処理など)がバグを含んでいないか、入念なレビューを実施する。
2-3. 出力層(アクチュエータ)の機構的共通故障
- 概要 スロットルアクチュエータや燃料噴射、点火系統などの出力段が、機構的に一つのモータやバルブに依存している場合、仮に電気的な二重化があっても、機械部品(モータ軸、ギア、バルブシャフト)の破断や固着が起きると両系統とも動作不能になり得る。
- 対策
- 機械的冗長化はコスト/スペース的に難しい場合が多いが、少なくともフェイルセーフ(バルブを閉方向にバネ戻しできる等)を備えて、過度な開度を防ぐ。
- アクチュエータが致命的に壊れたときでも、車両を安全側へ導けるように“上位の安全コンセプト”を明確化しておく(例: エンジンが止まっても制動/操舵が可能、など)。
3. CCFの評価と対策(ISO 26262でのアプローチ)
ISO 26262では、CCFを考慮するために以下のようなアプローチが推奨されています。
3-1. 安全ゴールの明確化
- 例えば「スロットルが意図せず全開にならないようにする」「ブレーキが効かない状態を回避する」などの安全目標に対して、冗長化だけでなくCCF対策も含めたアーキテクチャが設計されているかを確認。
3-2. FMEDA/FTA (故障モード影響解析 / フォルトツリー解析)
- 個々の要素に対して、どんな故障モードがあるかを洗い出し、共通要因故障が起こりうる経路を特定する。
- その原因や発生頻度を見積もり、対策の導入可否や効果を検討。
3-1. 3. SEooC (Safety Element out of Context) の適切な利用
- 他のプロジェクトやベンダーが提供する「安全認証済み部品」を活用する場合でも、自システム特有の環境(温度、振動、電磁環境など)でCCFリスクが高まらないかを確認する。
3-1. 4. バリエーション解析 (Diversity Analysis)
- ソフトウェアアルゴリズム、ハードウェアアーキテクチャ、製造プロセスなど、多様化をどこまで実施するか。
- コスト・開発期間を考慮しながら、一定の多様化を取り入れてCCFの確率を現実的に低減。
4. まとめ
2エレメント(メイン系・モニタ系)間のCCF
- ソフトウェアバグ、ハードウェアシリコンバグ、電源・ノイズ起因などにより、両系統が同時に誤作動する可能性はゼロではありません。
- 多様化設計や電源分離・ノイズ対策を行い、共通要因による故障を極力低減します。
3層(入力層・制御層・出力層)間のCCF
- センサ配線の共通断線、制御層共通部品(クロック、リセット回路)の不良、アクチュエータの機構的破損などで複数層が同時に機能不全になるリスクがあります。
- 層ごとに物理的・論理的分離や診断機能を強化し、単一点障害が多層へ波及するのを防ぎます。
したがって「2エレメント」や「3層構造」によって冗長性は高まりますが、CCFの可能性が完全になくなるわけではありません。ISO 26262の要求に則り、CCFのリスクを洗い出した上で、ソフトウェア多様化・物理的分離・冗長設計・適切な診断(フェイルセーフ)などの対策を適切に組み合わせることが重要です。
ChatGPT の回答は必ずしも正しいとは限りません。重要な情報は確認するようにしてください。