論文$\dagger$の続きです。
次はMPFに移ります。MPFの議論には一部正しい部分が見られます。それは、
- MPF,DPに分類されるフォールトはτにおいて全て修理される
- MPF,Lに分類されるフォールトは一切故障修理されない
これらは2nd SMの機能が働くSMのフォールトの扱いとしては全く正しいです。従って、
$$
F_\text{AVG,M}=\frac{1}{2}\tau\lambda_\text{MPF,DP}+\frac{1}{2}T\lambda_\text{MPF,L}
$$
は先に故障するSMの不信頼度としては正しいです。ところがIFとSMの区別に改善の余地があるように思われるので、その点が残念です。なぜならVSGに対してIFとSMのフォールトの効果は異なるからです。
これがSMの不信頼度であることを明確にすれば、添え字にSMを加え、
$$
F_\text{AVG,SM,M}=\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L}
$$
となります。
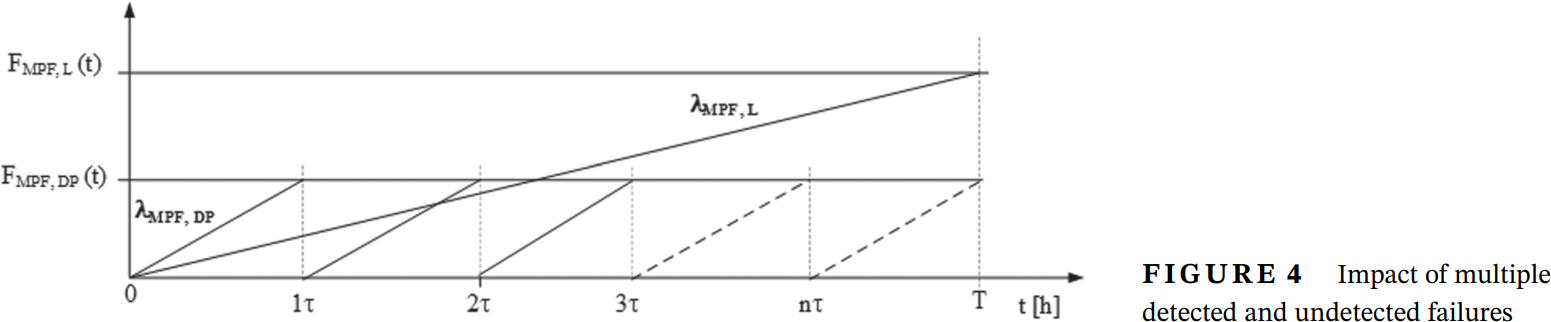 図743.1 2つの不信頼度MPF,DP/MPF,Lのグラフ
図743.1 2つの不信頼度MPF,DP/MPF,Lのグラフ
図743.1もSMの不信頼度のグラフと理解すれば全く正しいグラフです。実際には両者$F_\text{MPF,L}$と$F_\text{MPF,DP}$のグラフを加え合わせたものが本来の不信頼度のグラフで、いわゆるsawtooth waveと呼ばれるものですが、あまり見たことがありません。
この後に1oo2のサブシステムの計算が続きますが、ここまでで十分誤っているためそれが重なるだけです。従ってここではそれを指摘しませんが、本来は1oo2というよりもIFとSMとSM2から構成されるサブシステムを考えるべきです。ただし冗長系は別とします。そのサブシステムはRBDが規格Part 10にも載っており、かつ規格にもPMHF式が掲載されています。それらを全く無視している点には改善の余地が有りそうです。
よって、以上から正しい不信頼度を求めると、先にSMが故障し、後でIFが故障する場合のDPFを考えると、
$$
F_\text{AVG}=F_\text{AVG,S}+F_\text{AVG,SM,M}F_\text{AVG,IF,M}=(\lambda_\text{SPF}+\lambda_\text{RF})T+\left(\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L}\right)\lambda_\text{IF,MPF}T\\
$$
よって、
$$
M_\text{PMHF}=\lambda_\text{SPF}+\lambda_\text{RF}+\left(\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L}\right)\lambda_\text{IF,MPF}\\
=\lambda_\text{SPF}+\lambda_\text{RF}+\frac{1}{2}\lambda_\text{IF,MPF}\left(\lambda_\text{SM,MPF,DP}\tau+\lambda_\text{SM,MPF,L}T\right)
$$
これはSMのみがリペアラブルという1st edition規格式に相当します。
論文の誤りが深刻なのは、当該論文の誤りに留まらず、誤りが拡大再生産されることです。リトラクトしなければ永久に誤りが拡大再生産され続けます。
$\dagger$J. Famfulik, M. Richtar et al, "Application of hardware reliability calculation procedures according to ISO 26262 standard," Qual. Rel. Eng. Int. 2020, pp. 1-15, doi: 10.1002/qre.2625
 前のブログ
次のブログ
前のブログ
次のブログ






