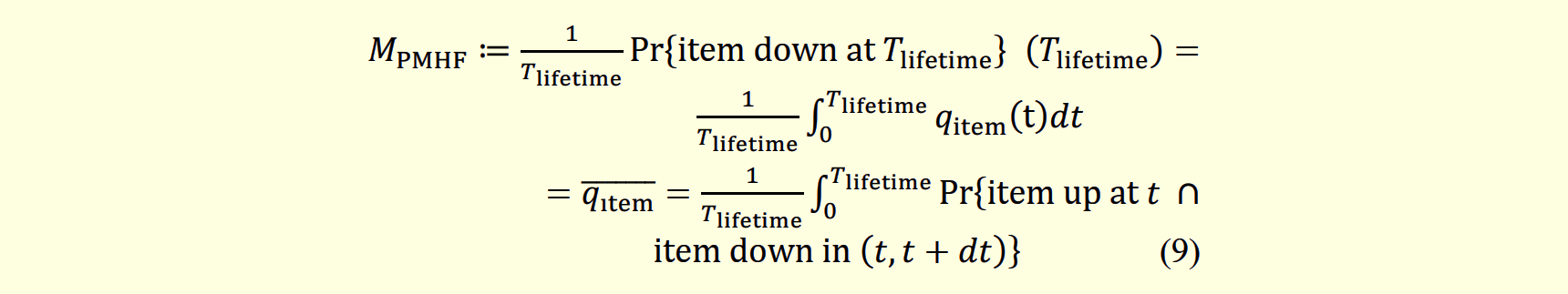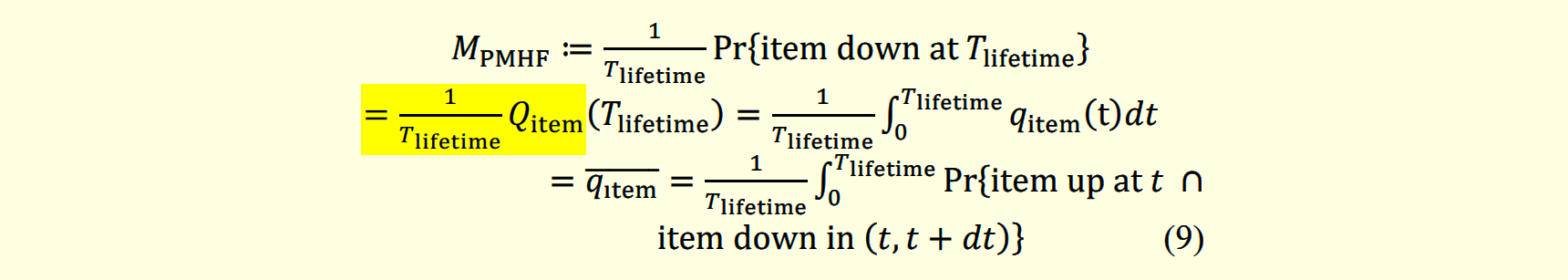|
3 |
弊社代表桜井 厚の論文がIEEE信頼性学会に2年連続採択 |
 |

ISO 26262機能安全(注1)コンサルティングを提供するFSマイクロ株式会社(本社:名古屋市)代表取締役社長 桜井 厚の論文が、2020年12月3日、IEEE(注2)主催の信頼性に関する国際学会である第67回RAMS 2021(注3)に採択されました。RAMS 2021は、2021年1月25日から28日まで、米国フロリダ州オーランドにて開催される予定です。同著者の論文がRAMSで採択されるのは、2020年1月に続いて2年連続となります。また、同著者は2017年に製品安全に関する国際学会である第14回ISPCE 2017(注4)において、最優秀論文賞を受賞しています。

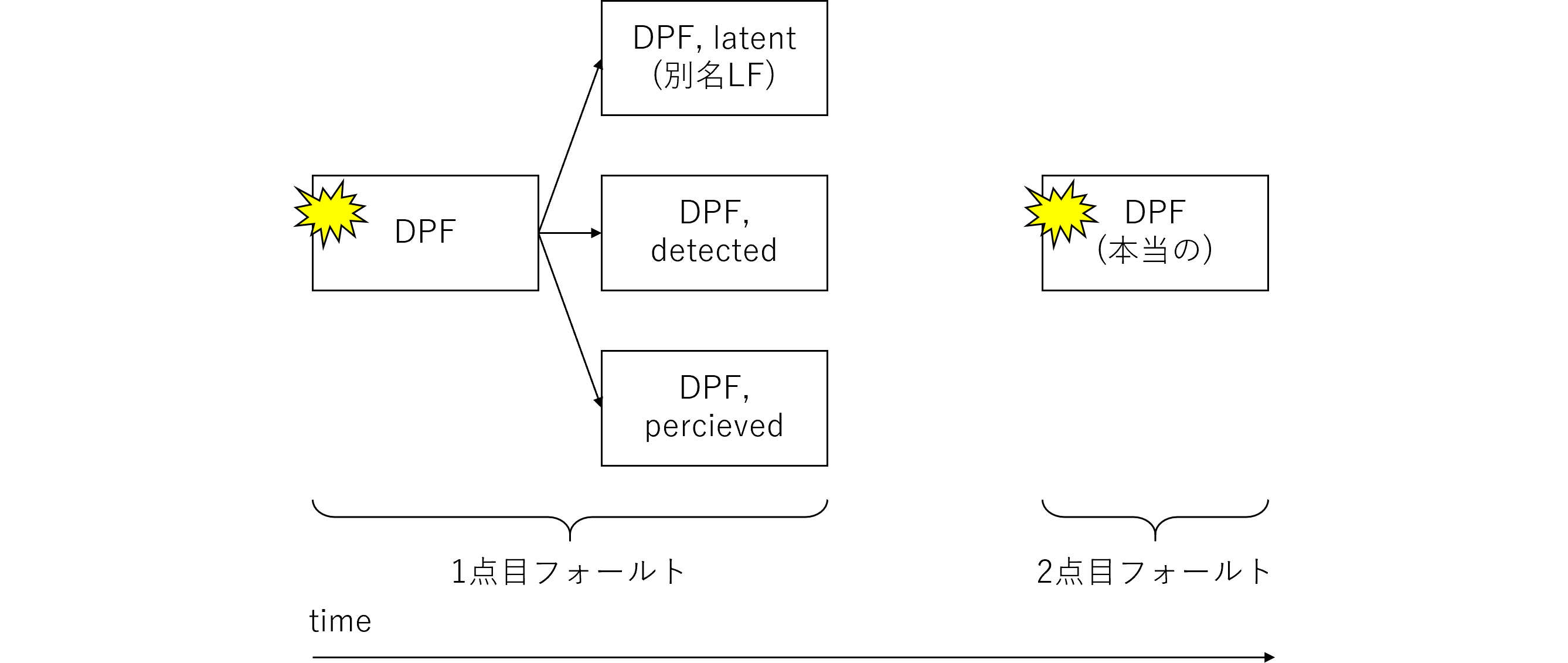
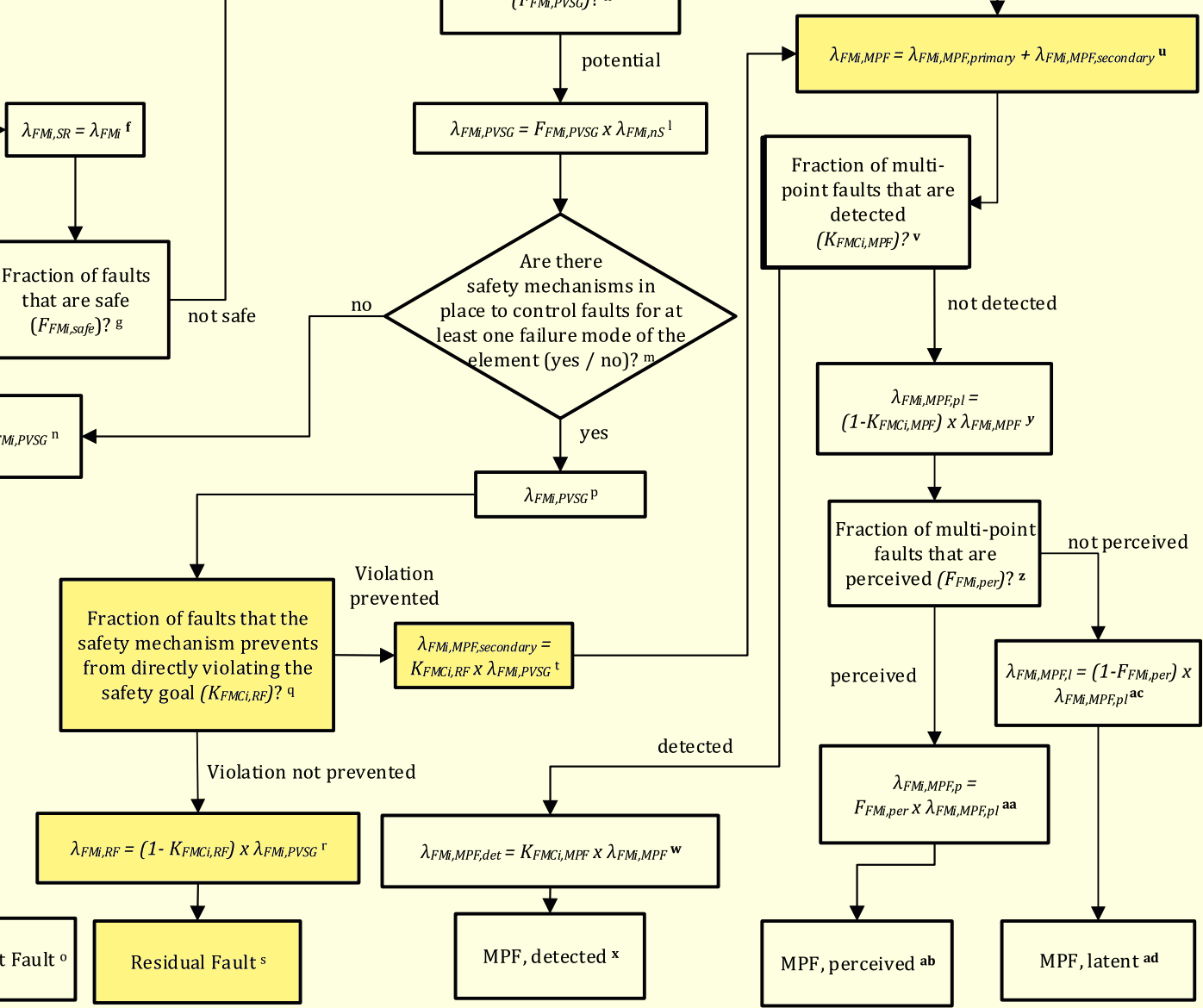
論文の題名は「A Framework for Performing Quantitative Fault Tree Analyses for Subsystems with Periodic Repairs」であり、邦題は「定期修理を伴うサブシステムにおける定量フォールトツリー解析のためのフレームワーク」です。本論文は、定量「フォールトツリー解析」(FTA, 注5)を用いて、車載電子機器の「ランダムハードウェア故障の確率的メトリクス」(PMHF, 注6)を正しく評価する手法を提案します。
2018年に、車載電子機器における機能安全の国際規格であるISO 26262の第2版が発行されました。この第2版にはPMHF式の数学的な定義は明確に記載されていません。さらに定量FTAの手法も明確ではないため、設計目標であるPMHF値を算出するためのガイドラインがありませんでした。
本論文は、2020年1月に開催されたRAMS 2020で同著者が発表したPMHF式に基づき、定量FTAを用いてPMHF値を算出するための具体的なフレームワークを提供します。それによりPMHF値の過小見積りを防止することが可能となります。本論文により、自動運転システムに代表される耐故障システム(注7)の安全性が向上し、故障による事故が抑止されることが期待されます。
【お問い合わせ先】
商号 FSマイクロ株式会社
代表者 桜井 厚
設立年月日 2013年8月21日
資本金 3,200万円
事業内容 ISO 26262車載電子機器の機能安全のコンサルティング及びセミナー
本店所在地 〒460-0011
愛知県名古屋市中区大須4-1-57
電話 052-263-3099
メールアドレス info@fs-micro.com
URL http://fs-micro.com/
【注釈】
注1:機能安全は、様々な安全方策を講じることにより、システムレベルでの安全性を高める考え方。ISO 26262は車載電気・電子機器を対象とする機能安全の国際規格
注2:IEEE(アイトリプルイー)は、Institute of Electrical and Electronics Engineersの略称。電気工学・電子工学技術に関する、参加人数、参加国とも世界最大規模の学会 https://www.ieee.org/
注3:RAMS(ラムズ)は、The 67th Annual Reliability & Maintainability Symposiumの略称。IEEE信頼性部会が毎年主催する、信頼性工学に関する国際学会 http://rams.org/
注4:ISPCE(アイスパイス)は、IEEE Symposium on Product Compliance Engineeringの略称。IEEE製品安全部会が毎年主催する、製品安全に関する国際学会 http://2017.psessymposium.org/
注5:FTA(エフティーエー)は、Fault Tree Analysisの略称。故障事象をツリー構造で構築し、安全目標侵害確率を算出することにより、危険事象の起きる可能性を定量的に論証する演繹的な安全分析手法
注6:PMHF(ピーエムエイチエフ)は、Probabilistic Metric for Random Hardware Failuresの略称。車載電気・電子システムにおいて、車両寿命間にシステムが不稼働となる確率を時間平均した、ハードウェアに関する設計目標値
注7:耐故障システムは、故障した場合に直ちに機能を失うことなく、本来の機能を代替することができる安全性向上のためのシステム