※前回の続きです。

設計制約

設計制約をリストアップします。

• LRCLKの1周期に対し、L=16bit, R=16bitの32bitのシリアルデータが必要であり、シリアルデータはSCKでシフトされるので、SCK=LRCLK*32。ただしこのSCKは、DACに供給しなければDAC内部で発生されます。
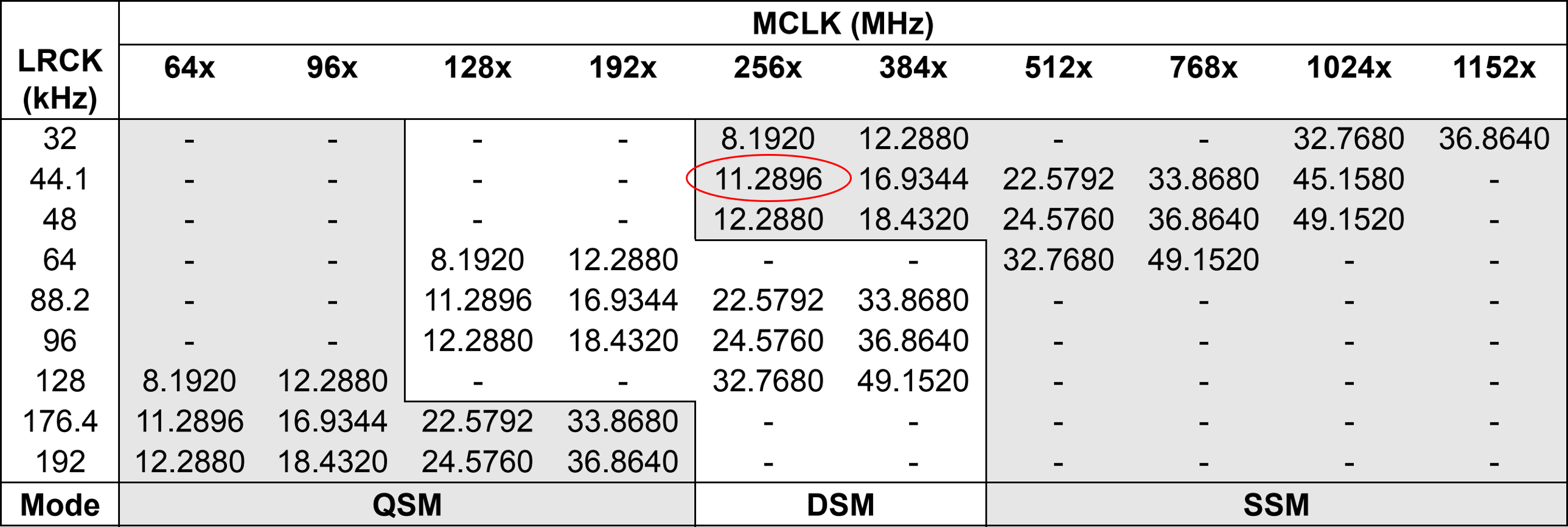
• データフォーマットより、サンプリングレートは16進数で16'h2b11=11025、すなわち11.025KHz。LRCLK=Fs(サンプリング周波数)とのことで、LRCLK=11.025KHzとしたいところですが、下図において、LRCLK=11.025KHzが存在しないので、データのほうを4倍のインターポレーションすることにし、LRCLK=44.1KHzとします。
• 上記関係式よりSCK=1.4112MHz。
• マスタークロック(MCLK)は下図のように、256, 384, 512, 768, 1024倍等の任意性がありますが、ここでは256倍のMCLK=11.2896MHzを使用します。

タイミングチャート

クロックに関する設計制約が解決したので、タイミングチャートを書いていきます。基本的にハードウェアベースのサウンド出力であるため、FSMによるフォーマット解析を行います。タイミングチャートは以下のとおりです。

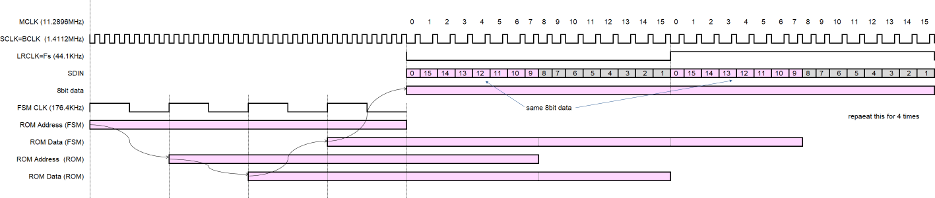
ステートマシンのクロックFSMCLKは図74.2のように、ステートアドレス、ステートデータ、データアドレス、データデータの4クロックで1サウンドデータの読み出しになることから、$\text{CLK}^{-1}$をCLKの周期と表記すれば、4*$\text{FSMCLK}^{-1}$=2*16*$\text{SCK}^{-1}$、つまり、8*FSMCLK=SCK。これよりFSMCLK=176.4KHz。

DACが要求する16bitデータ×2ch(L, R)の32bitデータについては、データソースが8bitモノラルであるため、8bitデータをMSB側に詰め、残りは0詰めし、16bitとします。LとRには同じデータを供給します。

インタポレーションのやり方はゼロ詰めする方法と、同じデータを繰り返す方法があります。16bit@44.1KHz表現可能なDACに対して8bit@11.025KHzという荒い音質であることから、同じ32bitデータを4回繰り返すことにします。

以上で設計制約から来るクロック周波数とタイミングチャートが確定したので、これに基づいてFSMを設計します。

前のブログ 次のブログ

冗長構成とは以下のように定義されます。

• 冗長構成 --- 機能的に対称な冗長。1oo2の冗長であり、2つのチャネルから成り、主系も従系もどちらも主機能を果たす一方、他方が故障した場合にVSGを抑止するSMの機能を果たす。

この冗長構成サブシステムにPMHFの値は2つあるのでしょうか?

具体例でみてみましょう。図のヘッドライト回路において、マイコンとトランジスタスイッチの両方からヘッドライトを点灯する機能があるとします。両者ともコンビネーションスイッチ情報を読み込み、点灯するものとします。さて、この場合、どちらが主機能でどちらが安全機構でしょうか？

この場合は冗長構成であるため、両方とも主機能となります。両方ともヘッドライト点灯という主目的をはたしているからです。一方で両方とも安全機構です。他方がフォールトしたときに、ライト消灯という、システムとしての機能喪失を抑止するためです。

具体的に数値を入れて見てみます。故障率をそれぞれ、スイッチ入力回路は1FIT、マイコンは100FIT、ドライバ出力回路は1FITとします。仮にマイコン側のチャネルを主機能、反対側をSMとし、主機能とSMの互いのSG侵害防止率を99%とすれば、PMHF第1式は、 $$ M_\mathrm{PMHF}=1.025FIT $$ となります。一方、どちらを主機能と見ても良いので、逆にすれば、 $$ M_\mathrm{PMHF}=0.015FIT $$ となります。このようにPMHFの値は2つあることになります。

しかしながら、設計意図の違いでアイテムのダウン確率が変わるはずがないため、これは明らかに誤りと分かります。論文で指摘したとおり、規格式が冗長に対応しておらず、MとSMに関して対称でないためです。

2nd Editionでは、MとSMに関して対称となっているので、本問題が解決されているように見えますが、既述のとおりある問題が残っています。

前のブログ 次のブログ

デュアルポイントフェイリャ

次にDPFについて、弊社が考える式とどこが相違しているかを見ていきます。

まず、SMがVSGとならない場合のパターン1式は特定条件(※1)でのみ合っています。この条件は1st Edition規格第1式とも同じです。次にパターン2は特定条件(※1)において前述のように2倍だけ異なっています。この2倍の理由は不明です。追記：4年後に判明したのでこの記事に記載しました。
※1 $K_{IF,lat}=0\cap K_{SM1,det}=1$の場合。これを言い換えると、IFはVSGの可能性があるが修理不可能、かつ、SM1はVSGの可能性無しで修理可能。

さらにパターン3、4式は特定条件(※2)でのみ合っています。単にパターン1, 2をひっくり返した(IFとSM1を入れ替えた)式のように見えます。
※2 $K_{SM1,lat}=0\cap K_{IF,det}=1$の場合。これを言い換えると、SM1はVSGの可能性があるが修理不可能、かつ、IFはVSGの可能性無しで修理可能。

これは以下の条件からくるものと推測します。以下は2nd Edition Part10 8.3.2.3 Table 2の引用です。

つまり、Pattern1及び2はIFフォールトによるVSGであり、SM1は修理系、IFは非修理系を仮定しています。 一方、Pattern3及び4はSM1フォールトによるVSGであり、Pattern1及び2のIF/SM1を入れ替えたものとなっているところから推測すればIFは修理系、SM1は非修理系を仮定しています。

いずれも最初のフォールトが起きるエレメントは、upしたりdownしたりを繰り返しても良いのですが(=修理可能という意味)、2番目にフォールトが起きるエレメントは、(最初のフォールトがリペアされた場合)downしたりupしたりするはずが、2番目にdownすることしか許されていません。これは非修理系を意味します。つまり後からフォールトするエレメントの制約が強すぎます。このことは言葉の定義だけで理解されるものではなく、その仮定から導出された1st Editionの式の意味まで考えて初めて理解されることです。

いずれにしろ、この前提はIFもSM1も$t=0$において修理系という一般的なサブシステムに対して、修理不可能という制約をかけすぎているため、PMHFの過大評価につながります。

弊社が考えるPMHFの一般式

IFとSM1が$t=0$において修理系という条件で、マルコフ状態遷移図を書き、確率微分方程式を立て、積分して平均PUDを算出した式において、Edition 1の方法で上界を求めた式は、 $$ M_{PMHF}=\lambda_{IF,RF}+\img[-1.35em]{/images/withinseminar.png}\tag{69.1} $$ となります。

規格の式(図68.1)は、実際よりも過剰な※1または※2のみで成立する式です。

前のブログ 次のブログ