On October 29, 2024, FS Micro Corporation※1 announced that a research paper by President and CEO Atsushi Sakurai has been accepted at RAMS※2, an international conference organized by the IEEE※3 Reliability Society.

This marks the sixth consecutive year that a paper by Atsushi Sakurai has been accepted at RAMS. The paper is scheduled for presentation at RAMS 2025, to be held on January 28, 2025, in Florida, USA.

This paper focuses on the PMHF※4 formula in ISO 26262※5. In ISO 26262, the PMHF is positioned as a critical metric for evaluating the safety of automotive systems, yet its derivation process is not thoroughly explained. Since 2011, Atsushi Sakurai has been addressing this issue and proposed a more accurate formula for the PMHF at RAMS 2020.

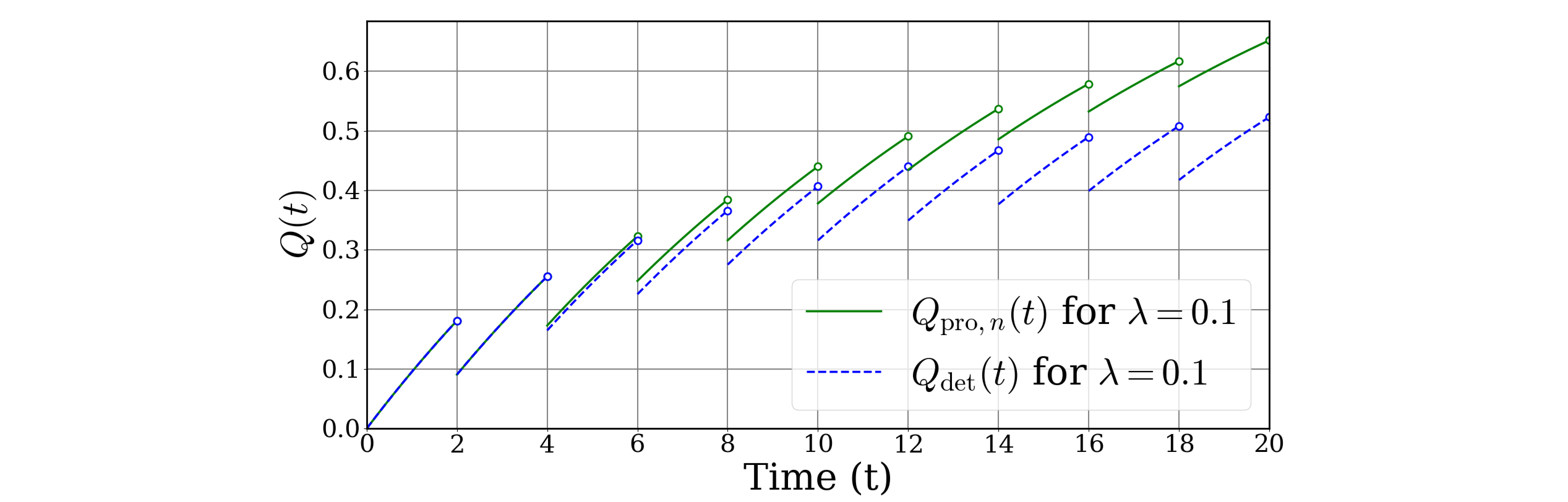
In this paper, the behaviors of the two stochastic processes, the PUA※6 and the PUD※7, under periodic inspection are analyzed in detail, and rigorous formulas for these processes are derived. Furthermore, the paper compares the rigorous formulas with the proposed approximate formulas, demonstrating the effectiveness of the approximate formulas in practical PMHF calculations.

The proposed PMHF formula provides higher accuracy while also allowing for improved design constraints. Therefore, this research is expected to make a significant contribution to enhancing the reliability of automotive systems.

Notes
※1: FS Micro Corporation (Headquarters: Nagoya, Japan; President and CEO: Atsushi Sakurai) is a consulting firm specializing in functional safety (a methodology for ensuring that equipment function correctly by implementing various safety measures) for automotive systems.
※2: RAMS (the Reliability and Maintainability Symposium) is an international conference on reliability engineering held annually by the IEEE Reliability Society. The 71st conference will take place in 2025. For more information: https://rams.org/
※3: IEEE is the abbreviation for the Institute of Electrical and Electronics Engineers, the world's largest professional technical organization dedicated to advancing technology. For more information: https://ieee.org/
※4: PMHF stands for Probabilistic Metric for Random Hardware Failures, a key metric under ISO 26262. It represents the time-averaged probability of hazardous system failures over a vehicle’s lifetime.
※5: ISO 26262 is an international standard for functional safety of automotive electronic and electrical systems, aiming to reduce the risk of hazardous events occurring while driving to an acceptable level due to system failures.
※6: PUA or the Point Unavailability, one of the stochastic processes that define the PMHF. It represents the probability that a system is in a failed state at a specific point in time.
※7: PUD or the Point Unavailability Density, another stochastic process that defines the PMHF. It represents the probability density of unavailability.

Contact Information
Company Name: 　　　　FS Micro Corporation
Representative: 　　　　 Atsushi Sakurai
Date of Establishment: 　August 21, 2013
Capital: 　　　　　　　　32 million yen
Business Description: 　Consulting services and seminars on functional safety for automotive electronic devices in compliance with ISO 26262
Head Office Address: 　 4-1-57 Osu, Naka-ku, Nagoya, Aichi 460-0011, Japan
Phone: 　　　　　　　　+81-52-263-3099
Email: 　　　　　　　　 info@fs-micro.com
URL: 　　　　　　　　　https://fs-micro.com/

前のブログ 次のブログ

2024年10月29日、FSマイクロ株式会社※1は、代表取締役桜井厚による論文が、IEEE※2 信頼性部会主催の国際学会RAMS※3 において採択されたことをお知らせします。

桜井厚の論文がRAMSに採択されるのは今回で6年連続となります。本論文は2025年1月28日に米国フロリダ州で開催されるRAMS 2025にて発表予定です。

本論文はISO 26262※4 のPMHF※5 公式に関する研究です。ISO 26262において、PMHFは車載システムの安全性を評価する重要な指標として位置づけられていますが、その導出過程は十分に説明されていません。桜井厚は2011年からこの課題に取り組み、RAMS 2020においてPMHFのより精度の高い式を提案しました。

本論文では、定期検査下での2つの確率過程であるPUA※6およびPUD※7の挙動を詳細に分析し、その厳密な公式を導出しています。さらに、厳密式と提案する近似式を比較検証し、近似式が実際のPMHF計算においても有効であることを示しました。

提案するPMHF式はより精度が高い式でありながら、設計制約の改善が見込めます。そのため、本研究を通じて、提案するPMHF式が自動車の信頼性向上に大きく貢献することが期待されます。

【注釈】
※1：FSマイクロ株式会社 (本社：名古屋市、代表取締役：桜井厚)は車載システムの機能安全(様々な安全方策を実施することにより、機器が正しく動作することを担保する方法論)に関するコンサルティングを提供する会社です。
※2：IEEEはInstitute of Electrical and Electronics Engineers(電気電子技術者協会）の略称で、技術の進歩を推進する世界最大の専門技術組織です。詳しくはhttps://ieee.org/
※3：RAMS(the Reliability and Maintainability Symposium)は信頼性・保守性シンポジウムの略称で、IEEE信頼性部会が毎年主催する信頼性工学に関する国際会議です。第71回の会議は2025年に開催されます。詳しくはhttps://rams.org/
※4：ISO 26262は車載電気電子システムの機能安全に関する国際規格で、システムの故障により車両の運転中に危険な事象が発生するリスクを許容できる水準まで低減することを目的としています。
※5：PMHFはProbabilistic Metric for Random Hardware Failures(ハードウェアのランダム故障に対する確率的指標)です。これはISO 26262におけるハードウェアの設計目標値の一つで、車両寿命間のシステム故障の時間平均確率を表します。
※6：PUAはPoint Unavailability(点不稼働度)の略で、PMHFを定義する確率過程の一つです。特定の時点でシステムが故障状態にある確率です。
※7：PUDはPoint Unavailability Density(点不稼働度密度)の略で、PMHFを定義する確率過程の一つです。点不稼働度の確率密度を示します。

【お問い合わせ先】
会社名　　　　 FSマイクロ株式会社
代表者　　　　 桜井 厚
設立年月日　　 2013年8月21日
資本金　　　　 3,200万円(資本準備金を含む)
事業内容　　　 ISO 26262車載電子機器の機能安全のコンサルティング及びセミナー
本店所在地　　 〒460-0011
　　　　　　　 愛知県名古屋市中区大須4-1-57
電話　　　　　 052-263-3099
メールアドレス info@fs-micro.com
URL　　　　　 https://fs-micro.com/

前のブログ 次のブログ

前記事#875のChatGPTの話す内容が数学的に若干おかしかったので、手動で修正しました。以下はChatGPTの出力を適宜修正したものです。

連続修理の場合：

稼働度$A(t)$は以下の式で表されます：

$$ A(t)=R(t)+\int_{0}^{t}m(x)\cdot R(t - x)\,dx $$

ここで、$R(t)$は時刻$t$での信頼度、$m(x)$は時刻$x$でのリニューアル密度です。$R(t-x)$は時刻$x$でリニューアルしたものが時刻$t$まで一度も故障しない確率です。

周期$\tau$の定期修理PIRの場合:

周期$\tau$のPIR(Periodic inspection and repair)戦略下では、修理が周期的に時刻$x=i\tau^-$($i=1,2,\dots,n$)で行われるため、この方程式は離散系となり次の式で表されます。

$$ A(t)=R(t)+\sum_{i=1}^{n}M(i\tau^-)\cdot R(t-i\tau^-) $$

ここで、$M(t^-)$は時刻$t$の直前における区間修理量です。

修理量は:

DC(Diagnostic coverage)を$K_\text{MPF}$で表せば、区間修理量$M(i\tau^-)$は区間累積故障の$K_\text{MPF}$倍となるため、区間修理量$M(i\tau^-)$は以下のようになります：

$$ M(i\tau^-)= K_{\text{MPF}}\int_{(i-1)\tau^+}^{i\tau^-}q(x) \, dx = K_{\text{MPF}} \left[ Q(i\tau^-) - Q\left( (i - 1)\tau^+ \right) \right] $$

ここで、

• $K_\text{MPF}$はDCであり定数、
• $q(t)$は不稼働密度関数(PUD)、
• $Q(t)=\int_{0}^{t}q(x)\,dx$は不稼働度関数(PUA)です。

不稼働度は：

$$ Q(t)=\img[-1.35em]{/images/withinseminar.png} $$

これにより、PIR戦略下の不稼働度PUAが陰関数形式で表されます。また、$Q(i\tau^+)$に関する一検査周期内の関係式を示します。

$$ \begin{eqnarray} Q(i\tau^+)&=&Q\left((i-1)\tau^+\right)+K_\text{MPF}\left[Q(i\tau^-)-Q\left((i-1)\tau^+\right)\right]\\ &=&(1-K_\text{MPF})Q((i-1)\tau^+)+K_\text{MPF}Q(i\tau^-) \end{eqnarray} $$

なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。

前のブログ 次のブログ

前の質問において何がReplay MemoryからDQN lossにインタフェースするのかが曖昧でかつタプル全部を渡すと誤った説明をしたため、確認します。

確かに、その指摘は正確です。次の状態$s'$は直接DQN損失関数の計算には使われず、実際にはTarget Q-networkに渡されて、そこで次の状態におけるすべての可能な行動$a'$に対するQ値の最大値$\max_{a'} Q(s', a'; \theta^-)$を計算するために使用されます。この最大Q値は、DQN損失関数の計算において、未来の報酬の推定値として利用されます。

リプレイメモリからDQN損失計算への直接的な情報

リプレイメモリからDQN損失計算に直接渡される情報は、以下の通りです：

1. 即時報酬$r$
2. 終了フラグ$done$

これらの情報は、DQN損失関数の計算に直接使用されます。

損失関数の計算に関わるその他のプロセス

1. 現在の状態$s$と行動$a$: これらはQ-networkを通じて、現在の行動価値$Q(s, a; \theta)$の計算に使用されます。
2. 次の状態$s'$: $s'$はTarget Q-networkに渡され、次の状態における最大の行動価値$\max_{a'} Q(s', a'; \theta^-)$を計算するために使用されます。この値は、損失関数の計算において間接的に使用され、未来の報酬の推定値として機能します。

DQN損失関数の計算式

DQN損失関数は、これらの要素を基に以下のように計算されます：

$$L(\theta) = \mathbb{E}\left[\left(r + \gamma \max_{a'} Q(s', a'; \theta^-) \cdot (1 - done) - Q(s, a; \theta)\right)^2\right]$$

ここで、$\gamma$は割引率です。この式は、即時報酬$r$と、未来の報酬の推定値$\gamma \max_{a'} Q(s', a'; \theta^-)$（ただしエピソードが終了した場合は0となる）、および現在の行動価値$Q(s, a; \theta)$に基づいています。

前のブログ 次のブログ

エージェントはそれ以外にも何があるかを聞いてみます。

ご指摘の通り、強化学習におけるエージェントの実装には、環境、Q-network、Target Q-network、DQN損失、Replay Memoryに加えて、ハイパーパラメータの管理やアルゴリズムの制御ロジックなど、さらに多くのコンポーネントや機能が必要になります。これらはエージェントの学習プロセスや意思決定プロセスの一部を形成し、効率的で効果的な学習を実現するために重要な役割を果たします。

エージェントの追加コンポーネントとその役割

1. ハイパーパラメータ管理:

   • 学習率、割引率、ε-greedy法のεなどのハイパーパラメータは、学習プロセスにおいて重要な役割を果たします。これらはエージェントの挙動を大きく左右し、最適化される必要があります。

2. 学習スケジュール:

   • 学習率やεの値を時間の経過とともに調整するためのスケジュールがあります。これらの動的な調整は、初期の探索と後期の利用のバランスを取るために不可欠です。

3. アルゴリズムの制御ロジック:

   • 学習プロセス（例えば、いつReplay Memoryからのサンプリングを行い、いつTarget Q-networkを更新するか）を制御するロジックが必要です。

エージェントとそのコンポーネント間のインタフェース信号

具体的なインタフェース信号や動作を数学的に表現するには、以下のような要素が含まれます：

• ハイパーパラメータ$ \alpha, \gamma, \epsilon $: $$ \text{学習率} \alpha, \text{割引率} \gamma, \text{探索率} \epsilon $$ これらは学習プロセスを制御し、特定の時間ステップや条件下で調整されることがあります。

• 制御ロジック: $$ \text{if } t \bmod N = 0 \text{ then } \theta^- \leftarrow \theta $$ ここで、$t$は時間ステップ、$N$はTarget Q-networkを更新する頻度です。

• 学習スケジュールに基づくハイパーパラメータの調整: $$ \epsilon \leftarrow \max(\epsilon_{\min}, \epsilon \times \text{decay_rate}) $$ 探索率$\epsilon$の調整例です。時間とともに$\epsilon$を減少させることで、初期の探索から後期の利用に重点を移します。

エージェントの実装には、これらのコンポーネントや機能が含まれ、それらの相互作用を通じて全体としての学習プロセスが構築されます。これらの詳細なインタフェース信号や制御ロジックを明確にすることは、効果的なエージェントの設計と実装において非常に重要です。

前のブログ 次のブログ

前記事からの続きです。

エージェントという言葉は環境以外の総体を指すようなので聞いててみます。

はい、その理解は正しいです。強化学習において、「エージェント」という用語は、学習アルゴリズム、意思決定プロセス、およびその他の学習を支援するメカニズム（Q-network、Target Q-network、Replay Memory、ハイパーパラメータ管理など）を含む総体を指します。環境を除くこれらすべてのコンポーネントが、一般的にエージェントの一部と見なされます。

エージェントの定義

エージェントは、以下を行うシステムまたはエンティティです：

• 環境からの入力（観測）を受け取る：エージェントは環境の現在の状態や、その状態に至るまでの履歴などの情報を受け取ります。
• 行動を選択し、実行する：エージェントは選択した行動を環境に対して実行し、その結果として状態が変化したり報酬を受け取ったりします。
• 学習を行う：エージェントは経験を通じて、より良い行動選択を行うための学習を行います。これには、獲得した報酬を最大化するようなポリシーを見つけるプロセスが含まれます。
• ポリシー（行動選択戦略）を改善する：エージェントは学習プロセスを通じて、ポリシーを継続的に改善し、最終的には目標を達成することを目指します。

環境との区別

エージェントと環境は、強化学習システムの二つの主要な要素です。環境はエージェントが操作し、その操作に対して報酬や新しい状態情報を提供する外部のシステムまたはプロセスです。エージェントと環境は相互作用を通じて互いに影響し合いますが、環境はエージェントによって制御されるわけではなく、そのダイナミクスはエージェントにとって与えられたものとなります。

結論

したがって、「エージェント」という用語は、環境以外の、学習と意思決定に関わるシステム全体を指すのに適切な言葉です。エージェントは、環境との相互作用を通じて、目的を達成するための最適なまたは満足のいく行動戦略を学習する役割を担います。

前のブログ 次のブログ

RAMS論文委員会の査読に対するレビューが完了し、指摘事項は無く、最終版(名前、所属有り)を10/17までに登録するようにという指示が来たので、早速登録しました。

これにより後は採択通知を待つのみです。

前のブログ 次のブログ