|
3 |
FTAのtree logic (3) |
 |
Posts Tagged with "ISO 26262"
既に発行済みのブログであっても適宜修正・追加することがあります。We may make changes and additions to blogs already published.
 |
2 |
FTAのtree logic (2) |
 |
 |
29 |
FTAのtree logic |
 |
 |
6 |
10月の検索結果 |
 |
弊社コンテンツの10月の検索結果です。
| タイトル | クリック数 |
|---|---|
| 故障分類 | +74 |
| SPFM, LFM, PMHFの計算法の例 | +72 |
| レイテントフォールトの奥深さ | +39 |
| タイトル | クリック数 |
|---|---|
| 1st Editionと2nd Editionとの相違点 (Part 10) | 226 |
| 機能安全用語集 | 199 |
| ASILデコンポジション | 115 |
| クエリ | クリック数 |
|---|---|
| FTTI | +27 |
| レイテント | +11 |
| FTTI FHTI | +9 |
| クエリ | クリック数 |
|---|---|
| FTTI | 107 |
| PMHF | 31 |
| SPFM | 23 |
 |
5 |
PMHFの導出の動画 |
 |
PMHFの算出法について以下の動画を見つけました。どうやらコンサル会社のビデオのようです。https://youtu.be/ndG1Kcc89hs
メディニアナライザを使用したようですが、PMHFの値は一見して誤っています。
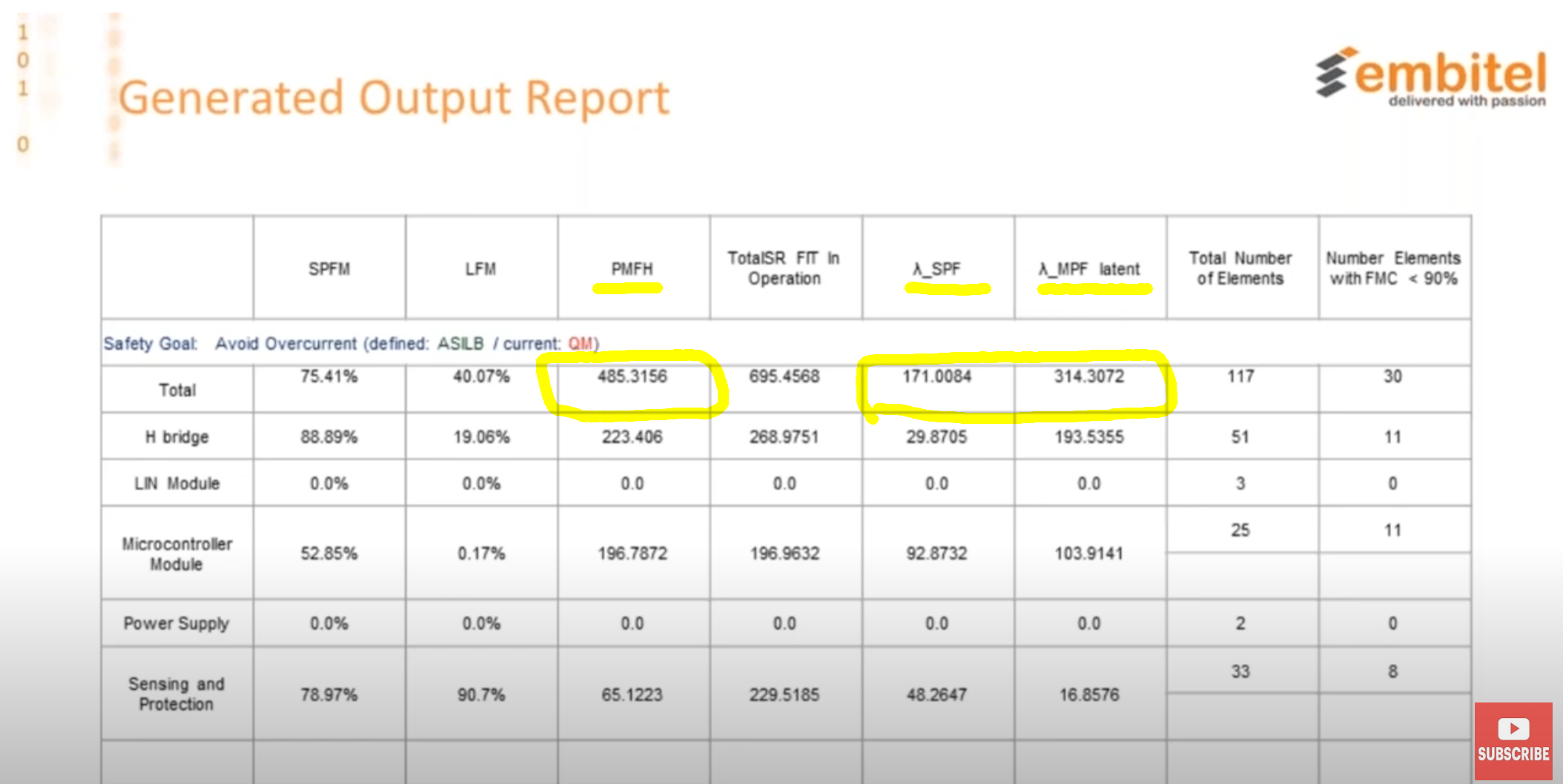
表の数値を見る限り、計算方法はSPFとDPFを加えて $$ PMHF=\lambda_\text{SPF}+\lambda_\text{MPF, latent} $$ となっているようです。
この誤りは大変多く、過去にも
- https://fs-micro.com/post/show/id/324.html
- https://fs-micro.com/post/show/id/325.html
- https://fs-micro.com/post/show/id/326.html
と複数あり、それらの誤りは以下の論文$\dagger$が元凶のようです。
一方、以下に前記事にもあるようにPart 5のAnnex Fに掲載されている近似式を示します。 $$ PMHF=\lambda_\text{SPF}+\lambda_\text{MPF, latent}\cdot\lambda_\text{MPF, detected}\cdot T_\text{lifetime} $$ この式はSPFとDPFをそれぞれを正しく確率に直してから加え、最後に車両寿命で割っています。そのことは両辺に車両寿命をかけると良く分かります。
それにしてもPMHFを算出する人たちはなぜ規格Part 10の、もしくはPart 5(上記)の式を用いずに、誤りの論文$\dagger$の式を参照するのでしょうか?参考にするならせめて規格式を参考にすれば良いと思うのですが。
$\dagger$ † Y. Chang, L. Huang, H. Liu, C. Yang and C. Chiu, "Assessing automotive functional safety microprocessor with ISO 26262 hardware requirements," Technical Papers of 2014 International Symposium on VLSI Design, Automation and Test, Hsinchu, 2014, pp. 1-4, doi: 10.1109/VLSI-DAT.2014.6834876.
 |
4 |
2nd SMのASILの引き下げ |
 |
備忘のために表題の「2nd SMのASILの引き下げ」について記します。ISO 26262ではセレクトハイ原則やFFI等の原則で、低ASILエレメントが高ASILエレメントに影響を及ぼすことが禁止されています。そのような場合は低ASILエレメントはASILを引き上げるべきです。
一方その原則の例外があり、有名なものは「ASILデコンポジション」です。ところでこの用語は厳密には正しくなく、本来は「要求分割(デコンポジション)により結果的にASILが分割される」ものであり、ASILを任意に分割するものではありません。
この他に表記の場合の例外があります。Part 4 6.4.2はシステム設計における安全機構の要件を示したもので、6.4.2.1及び6.4.2.2が「フォールトを検出及び機能安全要求を侵害するシステムの出力に存在する故障を防止又は緩和する安全機構」、つまり1st SMについての要件です。さらに6.4.2.3~6.4.2.5が「フォールトがレイテント状態になるのを防止する安全機構」、つまり2nd SMについての要件です。
ここで6.4.2.5において、2nd SMとしてのみ働くエレメントのASILは以下のように引き下げることが可能と書かれています。以下は規格に書かれていない文言をカッコ内に補って記述しています。
Part 4 - 6.4.2.5
- (IFまたは1st SMに)割りつけられた安全要求のASILがASIL-Dのとき、その2nd SMはASIL-B
- (IFまたは1st SMに)割りつけられた安全要求のASILがASIL-BまたはASIL-Cのとき、その2nd SMはASIL-A
- (IFまたは1st SMに)割りつけられた安全要求のASILがASIL-Aのとき、その2nd SMはQM
すなわち、ASIL-Bを除きASILを2段階引き下げることが可能です。ASIL-Bの時は1段階となります。
 |
30 |
FS Micro CEO Atsushi Sakurai's Paper Accepted for the Sixth Consecutive Year at International Reliability Engineering Conference |
 |

On October 29, 2024, FS Micro Corporation※1 announced that a research paper by President and CEO Atsushi Sakurai has been accepted at RAMS※2, an international conference organized by the IEEE※3 Reliability Society.
This marks the sixth consecutive year that a paper by Atsushi Sakurai has been accepted at RAMS. The paper is scheduled for presentation at RAMS 2025, to be held on January 28, 2025, in Florida, USA.

This paper focuses on the PMHF※4 formula in ISO 26262※5. In ISO 26262, the PMHF is positioned as a critical metric for evaluating the safety of automotive systems, yet its derivation process is not thoroughly explained. Since 2011, Atsushi Sakurai has been addressing this issue and proposed a more accurate formula for the PMHF at RAMS 2020.
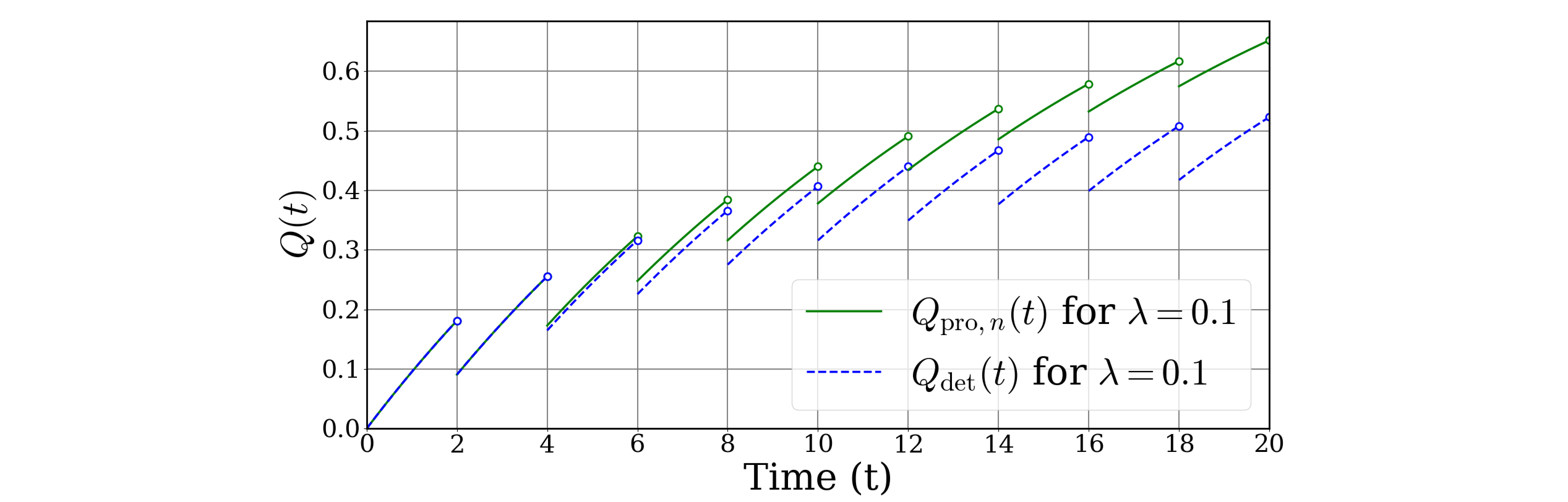
In this paper, the behaviors of the two stochastic processes, the PUA※6 and the PUD※7, under periodic inspection are analyzed in detail, and rigorous formulas for these processes are derived. Furthermore, the paper compares the rigorous formulas with the proposed approximate formulas, demonstrating the effectiveness of the approximate formulas in practical PMHF calculations.
The proposed PMHF formula provides higher accuracy while also allowing for improved design constraints. Therefore, this research is expected to make a significant contribution to enhancing the reliability of automotive systems.
Notes
※1: FS Micro Corporation (Headquarters: Nagoya, Japan; President and CEO: Atsushi Sakurai) is a consulting firm specializing in functional safety (a methodology for ensuring that equipment function correctly by implementing various safety measures) for automotive systems.
※2: RAMS (the Reliability and Maintainability Symposium) is an international conference on reliability engineering held annually by the IEEE Reliability Society. The 71st conference will take place in 2025. For more information: https://rams.org/
※3: IEEE is the abbreviation for the Institute of Electrical and Electronics Engineers, the world's largest professional technical organization dedicated to advancing technology. For more information: https://ieee.org/
※4: PMHF stands for Probabilistic Metric for Random Hardware Failures, a key metric under ISO 26262. It represents the time-averaged probability of hazardous system failures over a vehicle’s lifetime.
※5: ISO 26262 is an international standard for functional safety of automotive electronic and electrical systems, aiming to reduce the risk of hazardous events occurring while driving to an acceptable level due to system failures.
※6: PUA or the Point Unavailability, one of the stochastic processes that define the PMHF. It represents the probability that a system is in a failed state at a specific point in time.
※7: PUD or the Point Unavailability Density, another stochastic process that defines the PMHF. It represents the probability density of unavailability.
Contact Information
Company Name: FS Micro Corporation
Representative: Atsushi Sakurai
Date of Establishment: August 21, 2013
Capital: 32 million yen
Business Description: Consulting services and seminars on functional safety for automotive electronic devices in compliance with ISO 26262
Head Office Address: 4-1-57 Osu, Naka-ku, Nagoya, Aichi 460-0011, Japan
Phone: +81-52-263-3099
Email: info@fs-micro.com
URL: https://fs-micro.com/
 |
29 |
FSマイクロ代表桜井厚の論文が信頼性工学の国際会議にて6年連続採択 |
 |

2024年10月29日、FSマイクロ株式会社※1は、代表取締役桜井厚による論文が、IEEE※2 信頼性部会主催の国際学会RAMS※3 において採択されたことをお知らせします。
桜井厚の論文がRAMSに採択されるのは今回で6年連続となります。本論文は2025年1月28日に米国フロリダ州で開催されるRAMS 2025にて発表予定です。

本論文はISO 26262※4 のPMHF※5 公式に関する研究です。ISO 26262において、PMHFは車載システムの安全性を評価する重要な指標として位置づけられていますが、その導出過程は十分に説明されていません。桜井厚は2011年からこの課題に取り組み、RAMS 2020においてPMHFのより精度の高い式を提案しました。
本論文では、定期検査下での2つの確率関数であるPUA※6およびPUD※7の挙動を詳細に分析し、その厳密な公式を導出しています。さらに、厳密式と既提案の近似式を比較検証し、近似式が実際のPMHF計算においても有効であることを示しました。
提案するPMHF式はより精度が高い式でありながら、設計制約の改善が見込めます。そのため、本研究を通じて、提案するPMHF式が自動車の信頼性向上に大きく貢献することが期待されます。

【注釈】
※1:FSマイクロ株式会社 (本社:名古屋市、代表取締役:桜井厚)は車載システムの機能安全(様々な安全方策を実施することにより、機器が正しく動作することを担保する方法論)に関するコンサルティングを提供する会社です。
※2:IEEEはInstitute of Electrical and Electronics Engineers(電気電子技術者協会)の略称で、技術の進歩を推進する世界最大の専門技術組織です。詳しくはhttps://ieee.org/
※3:RAMS(the Reliability and Maintainability Symposium)は信頼性・保守性シンポジウムの略称で、IEEE信頼性部会が毎年主催する信頼性工学に関する国際会議です。第71回の会議は2025年に開催されます。詳しくはhttps://rams.org/
※4:ISO 26262は車載電気電子システムの機能安全に関する国際規格で、システムの故障により車両の運転中に危険な事象が発生するリスクを許容できる水準まで低減することを目的としています。
※5:PMHFはProbabilistic Metric for Random Hardware Failures(ハードウェアのランダム故障に対する確率的指標)です。これはISO 26262におけるハードウェアの設計目標値の一つで、車両寿命間のシステム故障の時間平均確率を表します。
※6:PUAはPoint Unavailability(点不稼働度)の略で、PMHFを定義する確率過程の一つです。特定の時点でシステムが故障状態にある確率です。
※7:PUDはPoint Unavailability Density(点不稼働度密度)の略で、PMHFを定義する確率過程の一つです。点不稼働度の確率密度を示します。
【お問い合わせ先】
会社名 FSマイクロ株式会社
代表者 桜井 厚
設立年月日 2013年8月21日
資本金 3,200万円(資本準備金を含む)
事業内容 ISO 26262車載電子機器の機能安全のコンサルティング及びセミナー
本店所在地 〒460-0011
愛知県名古屋市中区大須4-1-57
電話 052-263-3099
メールアドレス info@fs-micro.com
URL https://fs-micro.com/
 |
28 |
新方式によるPUAの導出 (12) |
 |
前記事#875のChatGPTの話す内容が数学的に若干おかしかったので、手動で修正しました。以下はChatGPTの出力を適宜修正したものです。
連続修理の場合:
稼働度$A(t)$は以下の式で表されます:
$$ A(t)=R(t)+\int_{0}^{t}m(x)\cdot R(t - x)\,dx $$
ここで、$R(t)$は時刻$t$での信頼度、$m(x)$は時刻$x$でのリニューアル密度です。$R(t-x)$は時刻$x$でリニューアルしたものが時刻$t$まで一度も故障しない確率です。
周期$\tau$の定期修理PIRの場合:
周期$\tau$のPIR(Periodic inspection and repair)戦略下では、修理が周期的に時刻$x=i\tau^-$($i=1,2,\dots,n$)で行われるため、この方程式は離散系となり次の式で表されます。
$$ A(t)=R(t)+\sum_{i=1}^{n}M(i\tau^-)\cdot R(t-i\tau^-) $$
ここで、$M(t^-)$は時刻$t$の直前における区間修理量です。
修理量は:
DC(Diagnostic coverage)を$K_\text{MPF}$で表せば、区間修理量$M(i\tau^-)$は区間累積故障の$K_\text{MPF}$倍となるため、区間修理量$M(i\tau^-)$は以下のようになります:
$$ M(i\tau^-)= K_{\text{MPF}}\int_{(i-1)\tau^+}^{i\tau^-}q(x) \, dx = K_{\text{MPF}} \left[ Q(i\tau^-) - Q\left( (i - 1)\tau^+ \right) \right] $$
ここで、
- $K_\text{MPF}$はDCであり定数、
- $q(t)$は不稼働密度関数(PUD)、
- $Q(t)=\int_{0}^{t}q(x)\,dx$は不稼働度関数(PUA)です。
不稼働度は:
$$ Q(t)=\img[-1.35em]{/images/withinseminar.png} $$
これにより、PIR戦略下の不稼働度PUAが陰関数形式で表されます。また、$Q(i\tau^+)$に関する一検査周期内の関係式を示します。
$$ \begin{eqnarray} Q(i\tau^+)&=&Q\left((i-1)\tau^+\right)+K_\text{MPF}\left[Q(i\tau^-)-Q\left((i-1)\tau^+\right)\right]\\ &=&(1-K_\text{MPF})Q((i-1)\tau^+)+K_\text{MPF}Q(i\tau^-) \end{eqnarray} $$
なお、本稿はRAMS 2025に投稿予定のため一部を秘匿しています。
 |
17 |
RAMS 2025へのマイルストーン (9) |
 |
RAMS論文委員会の査読に対するレビューが完了し、指摘事項は無く、最終版(名前、所属有り)を10/17までに登録するようにという指示が来たので、早速登録しました。
これにより後は採択通知を待つのみです。
| 期限 | マイルストーン | 状態 |
|---|---|---|
| 2024/5/3 | アブストラクト投稿締め切り(システム入力) | 投稿済 |
| 2024/6/10 | アブストラクト採択結果 | 採択済 |
| 2024/7/15 | 論文、プレゼン投稿締め切り(名前、所属無し版) | 投稿済 |
| 第1回論文、プレゼン資料査読コメント受領 | 投稿済 | |
| 2024/10/4 | 学会出席登録締め切り | 登録済 |
| 最終論文、プレゼン投稿締め切り(名前、所属有り版) | 登録済 |
ページ: