 |
21 |
$Q(t)$とChatGPT (17) |
 |
人間:
$Q(t)=(1−K_\text{MPF})F(t)+K_\text{MPF}F(u)$、ただし$F(t)$は不信頼度であり、$F(t)=1-e^{-\lambda t}$。また$u=t-n\tau$、$\tau$は検査周期、$n=\lfloor\frac{t}{\tau}\rfloor$であるとき$Q(t)$のグラフを描いてください。
ChatGPT:
まず、与えられた情報から数式を整理し、Pythonで使用できる形にまとめましょう。
- $ F(t) = 1 - e^{-\lambda t} $ は不信頼度(unreliability)関数です。ここで、$ \lambda $ は故障率です。
- $ u = t - n\tau $ は最後の検査からの経過時間を表します。ここで、$ \tau $ は検査周期、$ n = \lfloor \frac{t}{\tau} \rfloor $ は検査回数を表します。
- $ Q(t) = (1 - K_{\text{MPF}})F(t) + K_{\text{MPF}}F(u) $ は修理による信頼度の改善を表す関数です。ここで、$ K_{\text{MPF}} $ は修理の効果を表します。
この情報を基に、特定のパラメータ値(例えば $ \lambda = 0.1, \tau = 5, K_{\text{MPF}} = 0.2 $)で $ Q(t) $ のグラフを描くことができます。
ただし、$ t $ の範囲を指定していないため、ここでは $ t = 0 $ から $ t = 50 $ の範囲でグラフを描くことにします。もし異なる範囲やパラメータ値を希望する場合は、お知らせください。
import numpy as np
import matplotlib.pyplot as plt
import math
# Parameters
lambda_ = 0.1
tau = 5
K_MPF = 0.2
# Functions
def F(t, lambda_):
return 1 - np.exp(-lambda_ * t)
def Q(t, lambda_, tau, K_MPF):
n = np.floor(t / tau)
u = t - n * tau
return (1 - K_MPF) * F(t, lambda_) + K_MPF * F(u, lambda_)
# Time range
t = np.linspace(0, 50, 500)
# Compute Q(t)
Q_t = Q(t, lambda_, tau, K_MPF)
# Plot
plt.figure(figsize=(10, 6))
plt.plot(t, Q_t, label='Q(t)')
plt.xlabel('Time (t)', fontsize=14)
plt.ylabel('Q(t)', fontsize=14)
plt.title('Graph of Q(t)', fontsize=16)
plt.legend()
plt.grid(True)
plt.show()
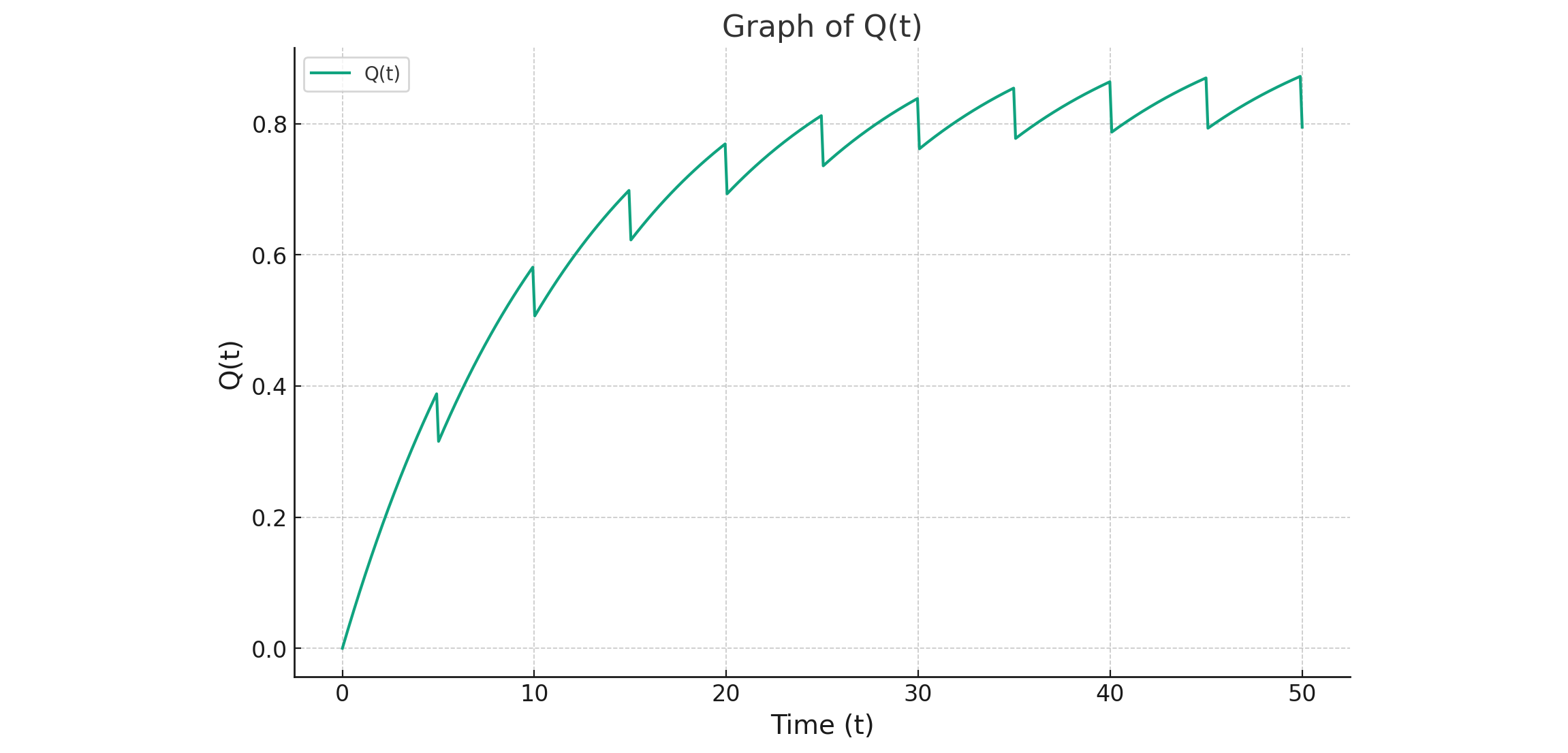
上記のグラフは、与えられたパラメータ($ \lambda = 0.1, \tau = 5, K_{\text{MPF}} = 0.2 $)と時間範囲 $ t = 0 $ から $ t = 50 $ における $ Q(t) $ の挙動を示しています。
$ Q(t) $ は時間とともに増加し、一定の検査周期 $ \tau = 5 $ 毎に信頼度が改善(リセット)されていることがわかります。これは、検査と修理が行われるたびにシステムの信頼度が高まることを表しています。
なお、上記のグラフは特定のパラメータ設定に基づいていますので、異なるパラメータ値や時間範囲でグラフを描くことも可能です。必要であれば、お知らせください。
- ChatGPTのコードインタプリターを用いました。
- 「$ u = t - n\tau $ は最後の検査からの経過時間を表します」という説明は少々驚きます。式を与えただけですが、ChatGPTは式の意味を正確に理解しています。
- 従来はグラフを描くのにプログラムを自分で作成するのは当たり前として、パラメータも全て指定する必要があったのが、AIにより全て全自動で書いて貰えるようになりました。ただし、プログラムやパラメータの妥当性は確認する必要があります。
