確率変数

次は(実数)確率変数の定義です。

確率変数$X$は標本空間$\Omega$の要素$\omega$に対して、実数値$x\in\mathbb{R}$(正確には$\mathbb{R}^n$)を写像する関数で、その逆像が$\Omega$の部分集合となるような可測関数です。

$$X:\omega\in\Omega\rightarrow x\in\mathbb{R}$$あるいはこれを簡単に $$X:\Omega\rightarrow\mathbb{R}$$ と表したとき、 $$X(\omega)=x\in\mathbb{R},\ X^{-1}(x)=\omega\in\Omega$$

実は、サイコロを振った事象をJupyter Notebookで表せるように$\{1, 2\}$等としていましたが、本来はサイコロ事象なので、$\{\img[-0.2em]{/images/d1s.png}, \img[-0.2em]{/images/d2s.png}\}$等とすべきでした。しかし、これでは計算が困難なため、(根元)事象を数値にマッピングすると便利です。その写像が上記で定義した確率変数です。

無故障稼働時間

具体例を示します。例えば確率変数がFFOT(Failure Free Operating Time; 無故障稼働時間)を表す時、部品が1,000個ある場合の故障状況をExcelでシミュレーションしてみます。ここで部品の故障率は皆同じで、$1.0\times 10^{-4}$とします。

図181.1 (1)の縦軸は1,000個の部品番号を示します。横軸は時間$t$[h]です。1,000個の部品が時間$t$に従って、ランダムに故障する状況を示しています。

図181.1 (2)はそれを故障した順番(つまりFFOTの短い順)にソートしたものです。

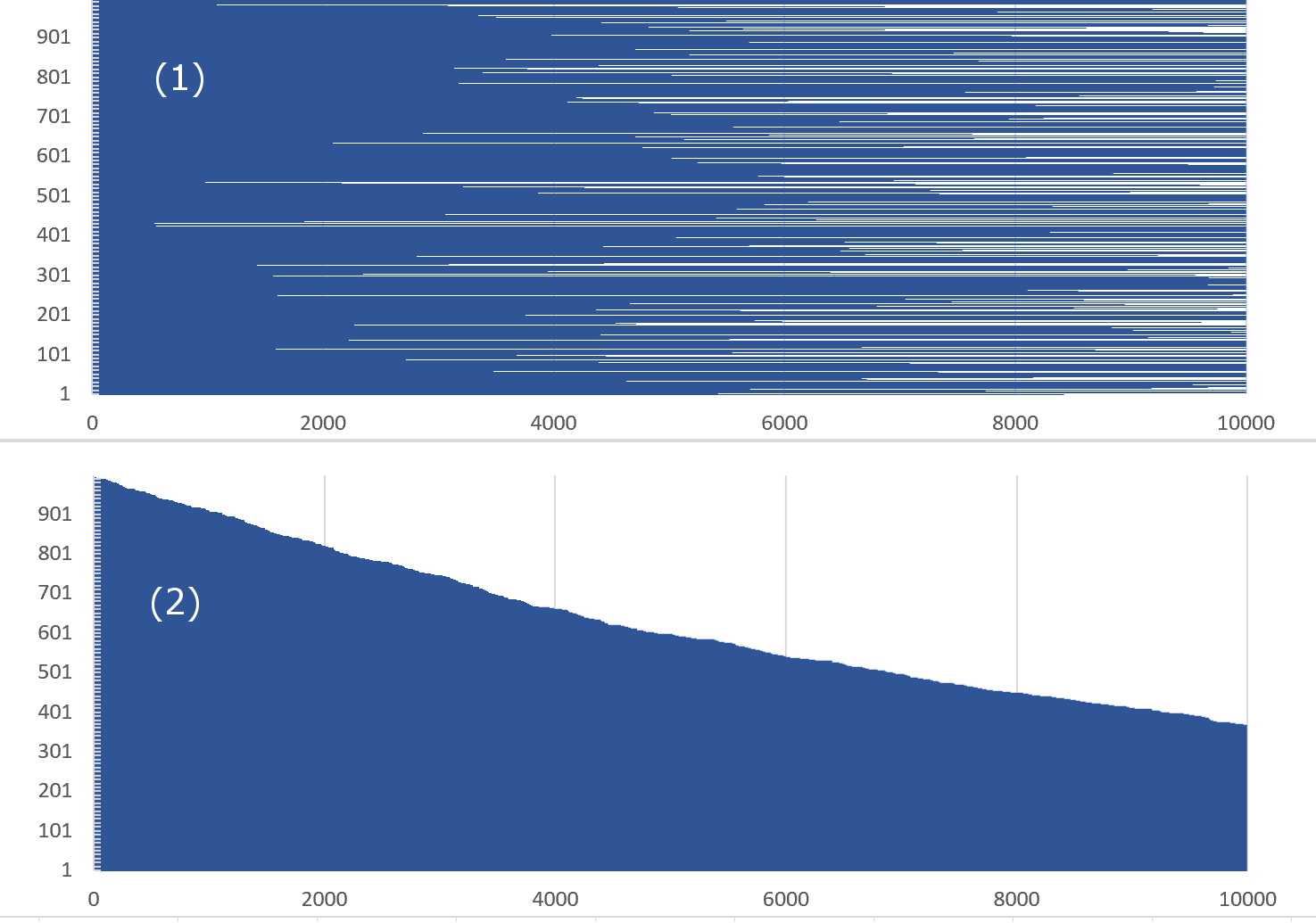
ここでは修理が無いため故障した部品はもう故障しないので、故障していない部品のみが故障することから、上記のFFOTの長さでソートすると、図181.1 (2)に示すとおり、一定の法則が見られます。これを確率分布(時間に関する確率分布は特に確率過程と呼ばれます)と呼び、故障率一定の場合は指数分布となります。

前のブログ 次のブログ