次は以下の論文です。

A. Köhler and B. Bertsche, “Cyclisation of Safety Diagnoses: Influence on the Evaluation of Fault Metrics,” 2021 Anuu. Rel. Maint. Symp. (RAMS), pp 1–7, Orlando, FL, USA, (Jan.) 2021.

アブストラクトの和訳を示します。

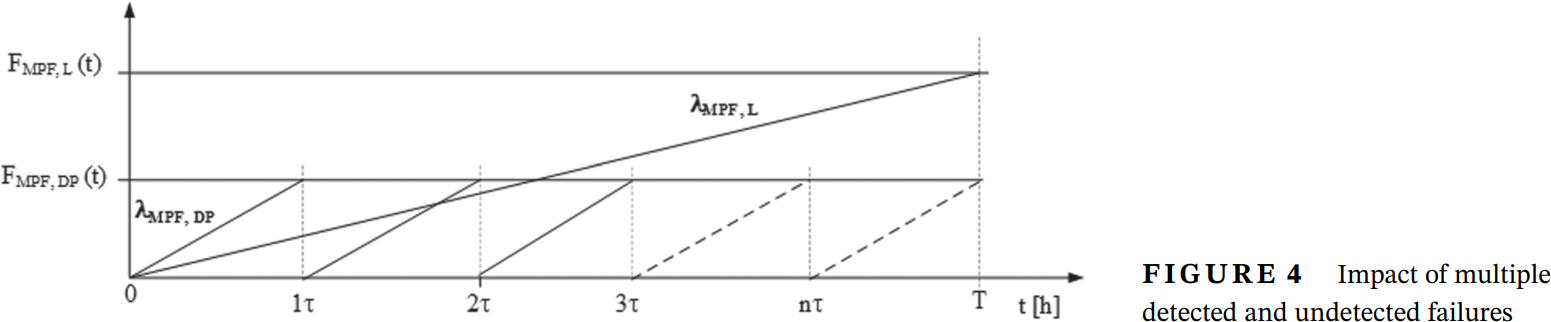
この技術的な詳細では、診断カバレッジ(DC)を伴う周期的安全対策に関連する意図された機能の確率的ハードウェア故障指標(PMHF)計算のための新しい数学的アプローチを導出する。これにより、指数故障分布の確率密度関数が安全診断の周期的影響に適応される、 さらに、適切な FTA モデルが説明される。これにより、PMHF 計算の現在のいくつかのアプローチが、対象とするユースケースに不適切であることが証明される。 分析と最新技術との比較により、このコンセプトの規範的・工学的な利点が示される： この新しい方法論は、車両パワーネットと安全診断の分野の例を用いて説明する。

このようにPMHF計算の新手法を提案しているようです。本当だったら大変に素晴らしいことですが、中身を見ていきます。

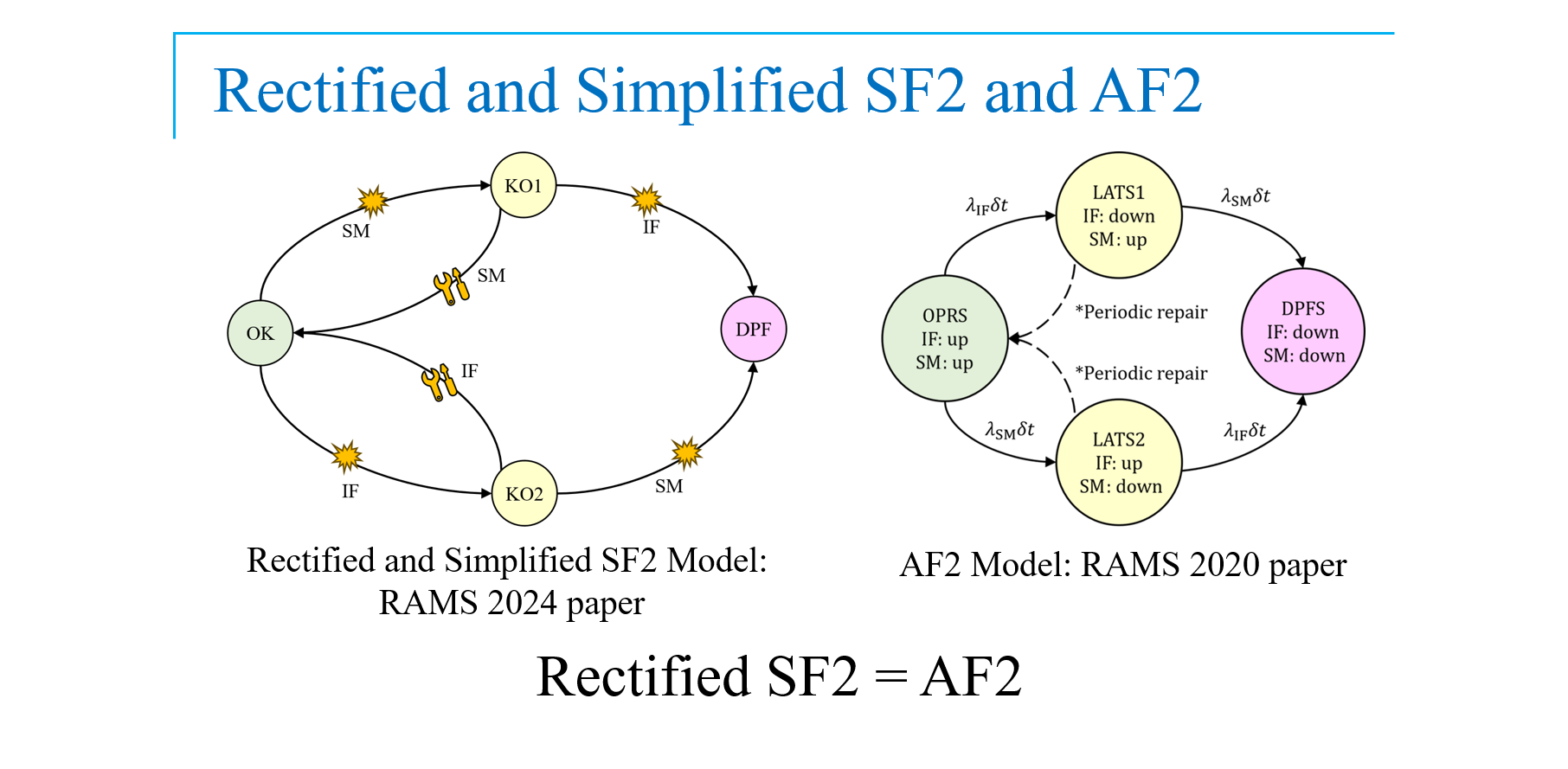
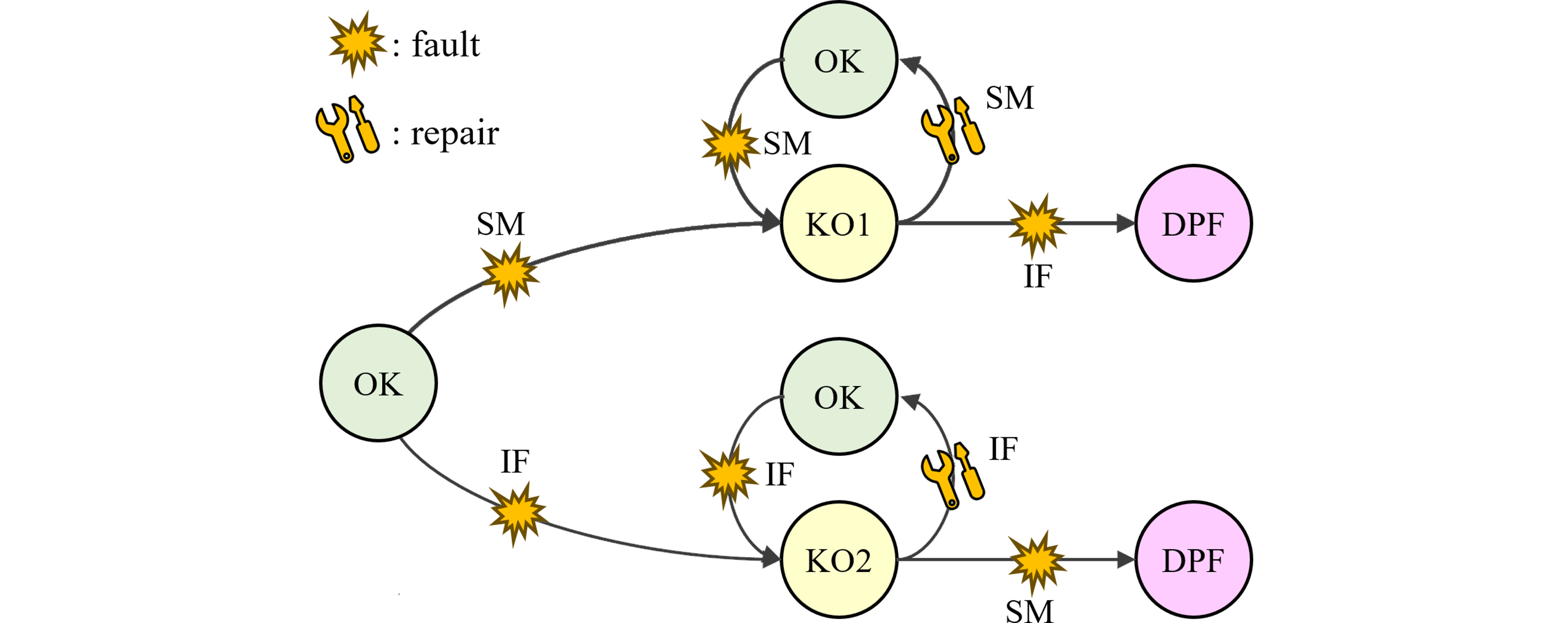
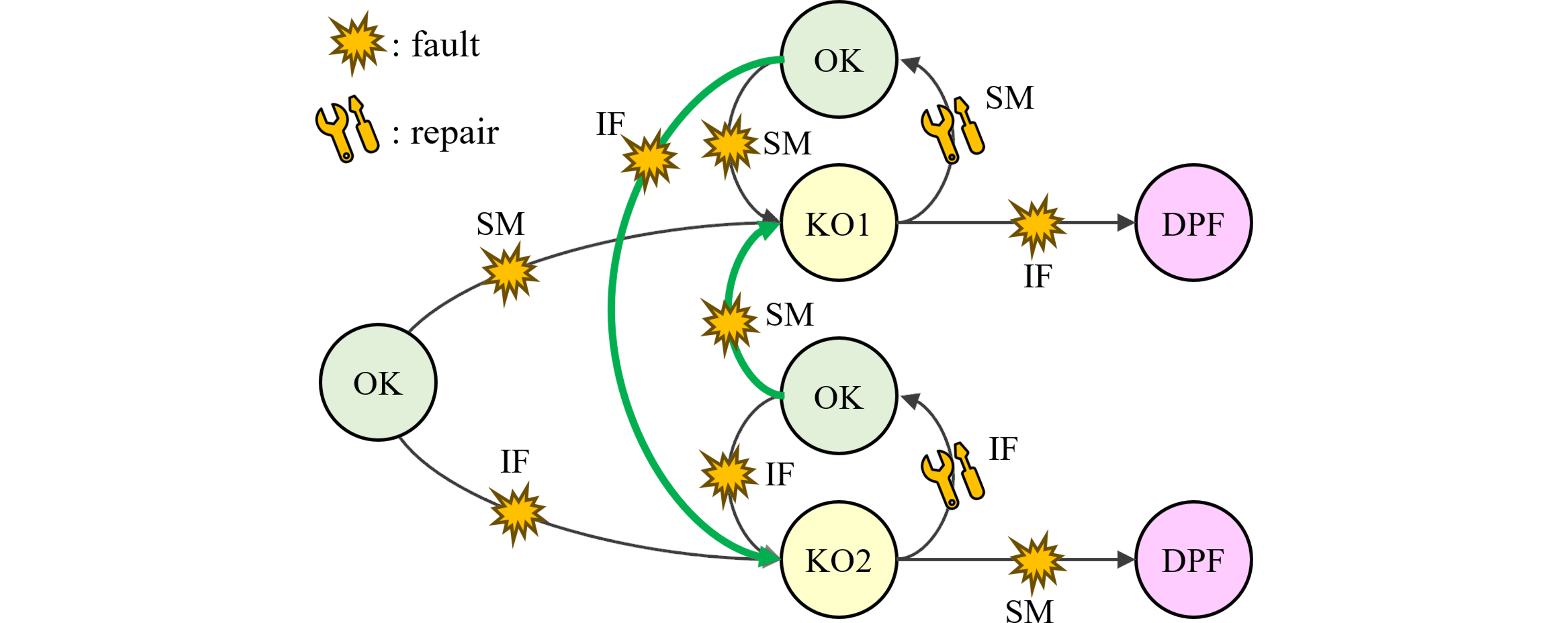
Those kind of diagnoses or safety measures, which have a significant influence of cyclisation, must not be treated as continuous systems in the safety validation process.
このような種類のサイクル化に大きな影響を与える診断や安全対策は、安全性検証プロセスにおいて連続システムとして扱ってはならない。

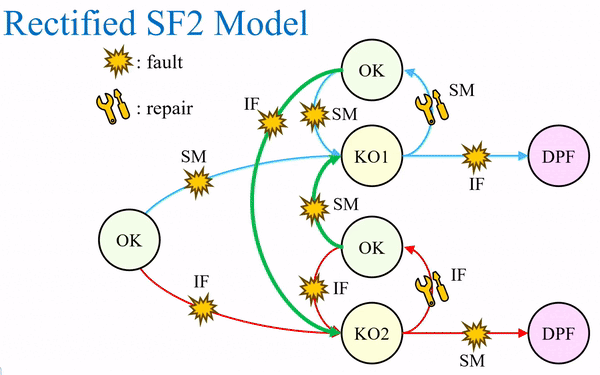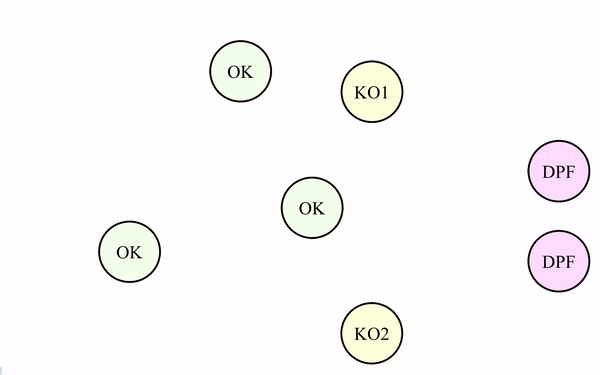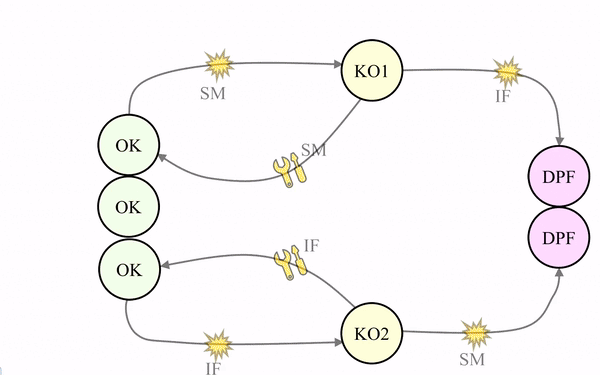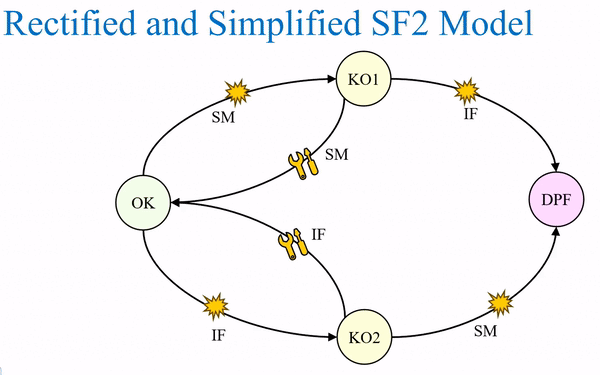
安全機構の種類については省略しますが、ここまでにおいて、この著者も1st SMと2nd SMの区別を記述していません。というのは

• 1st SMであれば、(真に連続的な診断ではないとしても)少なくともFTTIを満足するレベルの十分に高速な診断が必要となるし、
• 2nd SMであれば、1時間以上の十分に離散的な診断でOK

だからです。

これはフォールトの性質が異なるからであり、

• フォールトがVSGに直結するIFのフォールトであれば即時(FTTI中)の診断だけでなく安全状態への移行が必要になるし、
• SMのフォールトであれば、それはレイテントフォールトであるため、1時間以上の余裕を持った診断で良く、さらにドライバーが車両を運転して修理工場に運ぶことでもなんら問題はありません。

周期的な故障検出といってもFTTIが対象なのか、MPFDIが対象なのかで議論が全く変わってきます。

前のブログ 次のブログ

論文$\dagger$の続きです。

次はMPFに移ります。MPFの議論には一部正しい部分が見られます。それは、

• MPF,DPに分類されるフォールトはτにおいて全て修理される
• MPF,Lに分類されるフォールトは一切故障修理されない

これらは2nd SMの機能が働くSMのフォールトの扱いとしては全く正しいです。従って、

$$ F_\text{AVG,M}=\frac{1}{2}\tau\lambda_\text{MPF,DP}+\frac{1}{2}T\lambda_\text{MPF,L} $$ は先に故障するSMの不信頼度としては正しいです。ところがIFとSMの区別に改善の余地があるように思われるので、その点が残念です。なぜならVSGに対してIFとSMのフォールトの効果は異なるからです。

これがSMの不信頼度であることを明確にすれば、添え字にSMを加え、 $$ F_\text{AVG,SM,M}=\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L} $$ となります。

図743.1もSMの不信頼度のグラフと理解すれば全く正しいグラフです。実際には両者$F_\text{MPF,L}$と$F_\text{MPF,DP}$のグラフを加え合わせたものが本来の不信頼度のグラフで、いわゆるsawtooth waveと呼ばれるものですが、あまり見たことがありません。

この後に1oo2のサブシステムの計算が続きますが、ここまでで十分誤っているためそれが重なるだけです。従ってここではそれを指摘しませんが、本来は1oo2というよりもIFとSMとSM2から構成されるサブシステムを考えるべきです。ただし冗長系は別とします。そのサブシステムはRBDが規格Part 10にも載っており、かつ規格にもPMHF式が掲載されています。それらを全く無視している点には改善の余地が有りそうです。

よって、以上から正しい不信頼度を求めると、先にSMが故障し、後でIFが故障する場合のDPFを考えると、

$$ F_\text{AVG}=F_\text{AVG,S}+F_\text{AVG,SM,M}F_\text{AVG,IF,M}=(\lambda_\text{SPF}+\lambda_\text{RF})T+\left(\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L}\right)\lambda_\text{IF,MPF}T\\ $$

よって、 $$ M_\text{PMHF}=\lambda_\text{SPF}+\lambda_\text{RF}+\left(\frac{1}{2}\tau\lambda_\text{SM,MPF,DP}+\frac{1}{2}T\lambda_\text{SM,MPF,L}\right)\lambda_\text{IF,MPF}\\ =\lambda_\text{SPF}+\lambda_\text{RF}+\frac{1}{2}\lambda_\text{IF,MPF}\left(\lambda_\text{SM,MPF,DP}\tau+\lambda_\text{SM,MPF,L}T\right) $$ これはSMのみがリペアラブルという1st edition規格式に相当します。

論文の誤りが深刻なのは、当該論文の誤りに留まらず、誤りが拡大再生産されることです。リトラクトしなければ永久に誤りが拡大再生産され続けます。

$\dagger$J. Famfulik, M. Richtar et al, "Application of hardware reliability calculation procedures according to ISO 26262 standard," Qual. Rel. Eng. Int. 2020, pp. 1-15, doi: 10.1002/qre.2625

前のブログ 次のブログ

論文$\dagger$の続きです。

筆者らの研究では、1st SMと2nd SMの間の区別が明確でないように見受けられ、SPF/RF/MPF,DP/MPF,Lを一緒に取り扱っています。本来は

• SPF/RFに分類されるフォールトは単一故障事象の確率として扱う
• MPF,DP/MPF,Lに分類されるフォールトは2点故障事象の確率として扱う

このように両者は区別して扱う必要があります。前者は1st SMにより抑止・検出されるフォールトであり、後者は2nd SMにより検出されるフォールトです。筆者はこれらの4つのフォールトをいずれも単一故障事象として加え合わせています(論文式15)。 $$ P_\text{MHF}=\frac{1}{2}\left[(\lambda_\text{SPF}+\lambda_\text{MPF,DP})+(\lambda_\text{RF}+\lambda_\text{MPF,L})\right] $$ 本来は2点故障(DPF)の事象の確率は二乗する必要があります。具体的にはIFの故障確率とSMの故障確率の乗算です。上の論文式(15)にはそれが漏れています。

次に、単一故障事象の修理可能性について、筆者らの解釈にはさらなる考察が必要かもしれません。

• SPFに分類されるフォールトはτにおいて全て修理されると誤解している
• RFに分類されるフォールトは一切故障修理されないと誤解している

正解から言えば、SPF/RFはいずれもシングルポイントフォールト(単一故障事象)に分類され、単一のフォールトによりVSGとなるため、修理する暇が無いため修理は全く関係ありません。ISO 26262においては修理は次ページで扱うLFのみに関係します。

SPF/RFの区分について、本来はDC(ダイアグカバレージ)が0の場合をSPFとし、DCが0でない場合をRFとしています。筆者らの区分がこの定義から逸脱している可能性があり、そのため以下の式 $$ F_\text{AVG,S}=\frac{1}{2}\tau\lambda_\text{SPF}+\frac{1}{2}T\lambda_\text{RF} $$ は誤りです。また、図742.1で示されるグラフ同じ誤りを持っています。誤りは上記のとおり

• SPF/RFとも単一故障事象であるのに、修理を前提としている点、及び
• SPF/RFの区分が本来SMの有無すなわちDCの値によるものを、修理の有無であると誤解している点です。

さらにIFの故障率とSMの故障率の区別も改善の余地が有りそうですが、敢えて区別しておらず、エレメント一般の故障率として扱い、後で1oo2の一般解を導くためのようです。

正解を故障確率で表すなら、 $$ F_\text{AVG,S}=(\lambda_\text{SPF}+\lambda_\text{RF})T $$ となります。いずれもIFの故障率です。なぜならSMのフォールトは単一ではVSGとならないからです。ここで$T$は車両寿命とします。

$\dagger$J. Famfulik, M. Richtar et al, "Application of hardware reliability calculation procedures according to ISO 26262 standard," Qual. Rel. Eng. Int. 2020, pp. 1-15, doi: 10.1002/qre.2625

前のブログ 次のブログ

PUAに関する論文が複数出ているので、その内容を確認します。

J. Famfulik, M. Richtar et al, "Application of hardware reliability calculation procedures according to ISO 26262 standard," Qual. Rel. Eng. Int. 2020, pp. 1-15, doi: 10.1002/qre.2625

以降翻訳はDeepLによるものです。まずアブストラクトを示します。

自動車産業における機能安全評価のための規格ISO 26262（2018年版）第2版では、ランダムハードウェア故障の確率的メトリック（PMHF）を使用したハードウェア評価が要求されている。この規格では、フォールトツリー解析（FTA）の活用を強く推奨しているが、具体的な計算例は示されていない。そこで、本稿では、電子システムのさまざまなハードウェア・アーキテクチャに対する数式の導出と説明を含む計算手順について説明する。記述されている数式は、多重故障の影響やelf-testの影響を考慮しているが、数式は比較的単純である。この単純さにより、ハードウェア設計の頻繁な変更が予想されるハードウェア開発の初期段階で使用することができる。したがって、ケーススタディを添付したこの論文は、科学者だけでなく、自動車産業における重要な安全関連電子システムの開発者を対象としている。

PMHFの数学的な定義を平均的な車両寿命間の不信頼度の時間平均とした論文の(3)式は

$$ P_\text{MHF}=\frac{F_\text{AVG}}{t} $$ と書かれています。改善点としては細かいことを言えば、PMHFの表記は規格Part 10に従えば$P_\text{MHF}$ではなく$M_\text{PMHF}$です。またPMHFは車両寿命間の時間平均故障確率であるため、分母は$t$ではなく、$T_\text{lifetime}$(論文中では大文字の$T$)です。

従って論文の(3)式は正しくは $$ M_\text{PMHF}=\frac{F_\text{AVG}}{T} $$

とすべきです。ここで問題は$F_\text{AVG}$は不信頼度の平均です。ところがこれはおかしく、$T$で割っていることが車両寿命間の時間平均を表すので、分子は積分値であるべきです。そのため筆者の平均値の認識には改善点があると言うべきです。これは以下の式にも認めることができます。論文の(5)式は

$$ F(t)=\lambda t $$ これは不信頼度の式で、非修理系においては正しい式です。ところが問題は次の$F_\text{AVG}$で、論文の(6)式は

$$ F_\text{AVG}=\frac{1}{t}\int_0^t F(t)dt $$ つまり、(6)式においてF(t)を平均化した後さらに(3)式において$T$で割るという2重に平均を取ることを行っています。

本来は、我々の記法に従えば、 $$ M_\text{PMHF}=Q_\text{AVG}=\frac{Q(T)}{T} =\frac{1}{T}\int_0^T q(t)dt $$ とするのが正しい方法です。ここで$Q(t)$はPUA, $q(t)$はPUDです。

以降では本論文がPMHFをどのように導出するかを見ていきます。

前のブログ 次のブログ

過去記事において不稼働度(Point Unavailability; PUA)を求めました。ここでは別の方式で不稼働度を求めてみます。

SMのフォールトが生起したとき、それがレイテントフォールトとなるかならないかは2nd SMの故障検出率で決定されます。これを$K_\text{SM,MPF}$とすると、従来は $$ K_\text{SM,MPF}=\Pr\{\text{detectable}\}\tag{740.1} $$ としてPUAである$Q(t)$を求めていました。

ここで新しく、 $$ K_\text{SM,MPF}=\Pr\{\text{detected }|\text{ failed at }t\}\tag{740.2} $$ この式(740.2)に基づいてPUAを導出します。これは、修理が完全に確率的に行われることを意味し、検出されるされないは故障の原因によらずにSMの能力のみに依存することになります。

不稼働度$Q(t)$の一般式

稼働度(Point Availability; PA)の公式から不稼働度は以下のように表せます。

$$ Q(t)=F(t)-\int_0^{T_\text{lifetime}}m(x)R(t-x)dx\\ =F(t)-\sum_{i=1}^nM(i\tau)R(t-i\tau)\tag{740.3} $$ 意味としては、フォールトが起きて累積していく分から故障が修理され、各修理分が現在まで生き残っている分を引いたものとなります。ここで$M(i\tau)$は定期修理点$i\tau$における修理率です。

Kパラメータの適用

さて、式(740.3)に式(740.1)を適用すれば、定期修理点$i\tau$における修理率$M(i\tau)$はその時点での不稼働確率$Q(i\tau)$に故障検出率を$K_\text{SM,MPF}$かけたものとなることから、

$$ Q(t)=F(t)-\sum_{i=1}^n K_\text{SM,MPF}Q(i\tau)R(t-i\tau)\tag{740.4} $$ このQ(t)は定期修理区間毎に変わるので、定期修理区間を$i=0,1,2,...$で表せば、

$$ \begin{eqnarray} \left\{ \begin{array}{l} Q_0(t)&=&0\quadただしt=0\\ Q_1(t)&=&F(t)\quadただしt\in(0, \tau]\\ Q_n(t)&=&F(t)-\sum_{i=1}^{n-1}K_\text{SM,MPF}Q_i(i\tau)R(t-i\tau)\quadただしt\ge\tau \tag{740.5} \end{array} \right. \end{eqnarray} $$

右辺に求めたい$Q(t)$を持つため、解析的に求めるのは困難であり、再帰的あるいは数値的に求めるしかありません。よってこれより次の$Q_2(t)$を求めれば、 この(740.4)式は誤りであり、再検討したこの記事に続きます。 $$ \begin{eqnarray} Q_2(t)&=&F(t)-K_\text{SM,MPF}Q_1(\tau)R(t-\tau)\\ &=&F(t)-K_\text{SM,MPF}F(\tau)R(t-\tau)\quadただしt\in(\tau, 2\tau] \tag{740.6} \end{eqnarray} $$

さらに次の$Q_3(t)$は、 $$ \begin{eqnarray} Q_3(t)&=&F(t)-K_\text{SM,MPF}Q_1(\tau)R(t-\tau)-K_\text{SM,MPF}Q_2(2\tau)R(t-2\tau)\\ &=&F(t)-K_\text{SM,MPF}\left[F(\tau)R(t-\tau)+\left(F(2\tau)-K_\text{SM,MPF}F(\tau)R(2\tau-\tau)\right)\right]R(t-2\tau)\\ &=&F(t)-K_\text{SM,MPF}\left[F(\tau)R(t-\tau)+\left(F(2\tau)-K_\text{SM,MPF}F(\tau)R(\tau)\right)R(t-2\tau)\right]\\ &&ただしt\in(2\tau, 3\tau] \tag{740.7} \end{eqnarray} $$ このようにかなり複雑な形になるため、実用的には数値計算することになります。

前のブログ 次のブログ

図738.3の修正したSF2モデルは過去論文でAF2を導出した際のCTMC図と見かけは異なりますが、同一であることを以下に証明します。

2つの分岐に橋を架けたことによりOKはそれぞれ同一状態となり、またDPFは元々同一状態であったので、このようにマージすることができます。

以上より、図739.2に示すように両者が実質は同一であることが証明できたため、そのモデルから得られるPMHF方程式は同一であることが証明されました。つまり、SF2の11か所の誤りを全て修正するとAF2となることが言えます。

前のブログ 次のブログ

RAMS 2024で発表した論文のプレゼンテーション資料から一部を示します。

SF2式

過去論文により冗長アーキテクチャに対応した新しいPMHF式を提案しました。これをここではAF2と呼びます。

$$ M_\text{PMHF}=(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\lambda_\text{IF}\lambda_\text{SM}\left[(1-K_\text{MPF})T_\text{lifetime}+K_\text{MPF}\tau\right]\\ s.t.\quad K_\text{MPF}:=K_\text{IF,MPF}+K_\text{SM,MPF}-K_\text{IF,MPF}K_\text{SM,MPF} \tag{AF2} $$

一方で、規格第2版に掲載の以下のPMHF式をSF2と呼ぶと、明らかに両者は異なります。

ここでAF2のSPF項である$(1-K_\text{IF,RF})\lambda_\text{IF}$とSF2のSPF項である$\lambda_\text{SPF}+\lambda_\text{RF}$は等しいため、AF2とSF2の違いはDPF項のみとなります。

両方の式どうしが等しいことを簡単に証明します。まず、$K_\text{IF,RF}=0$とするとこれはSMが存在しない場合を表し、$\lambda_\text{SPF}=\lambda_\text{IF}$です。次に$K_\text{IF,RF}\ne0$の場合は、$\lambda_\text{RF}=(1-K_\text{IF,RF})\lambda_\text{IF}$であり、これはRFの定義式です。

SF2の状態遷移図

我々は2019年に日本で発行された第2版規格式の解説書により、SF2の導出過程には11か所の誤りがあることを識別しました。それを全て修正したものがAF2となることを今回のRAMS 2024で発表しました。最も重大な誤りであるステート遷移の誤りについてここに示します。

図738.1は規格式SF2の元になったと推測されるステート遷移図です。ただしこれは規格に書かれているわけではなく、図738.1のSF2から逆に求めた状態遷移図であることに注意が必要です。

修正したSF2の状態遷移図

規格のステート遷移図はIFとSMのリペアビリティが誤っていると考えるため、弊社では図738.3のようにグリーンで橋渡しを行い、SF2モデルを修正しました。弊社の考える規格の誤りは、初期のOK状態からIFもしくはSMの一方が非修理となっている点です。本来はIFもSMもリペアラブルでなくてはならないと考えます。

図738.2が図738.1のとおり、4つのパターンにしか対応していないのに対して、図738.3は無限のパターンに対応している点が異なります。

両者のリペアラビリティの違い

規格によるパターン分析は、DPFにおいて、SM⇒IFもしくはIF⇒SMの引き続くフォールト順の2つにケース分けをしている点で正しいように見えますが、修理順が誤っています。図738.2のように一旦SMのフォールトが起きると、それがリペアされても初期状態には戻らず、次はSMのフォールトしか許されていません。

一方、弊社の修正によれば図738.3のように、一旦リペアされればSMのフォールトでもIFのフォールトでも生起することが可能です。これが本来の意味のIFとSMのリペアラブルという意味です。

ただし、一見すると状態遷移図が複雑になったように見えます。

前のブログ 次のブログ

過去記事に記載のとおり、RAMS 2024は、2024年1月22日から25日まで、米国ニューメキシコ州アルバカーキのクライドホテルで開催されました。弊社代表は最終日に論文発表を行いました。

本論文のタイトルは、"Identifying and Rectifying the Potential Faults in the Probabilistic Metric (PMHF) Formula in ISO 26262"です。邦題は「ISO 26262における確率的メトリック式（PMHF）の潜在的フォールトの特定と修正」となります。潜在的フォールトもしくはシステマティックフォールトとは規格用語であり、一般的には、エラーとか誤りとか呼ばれる欠陥を意味します。

本論文は規格PMHF式の導出過程を分析することでPMHF式の問題点11か所を識別します。さらにそれらの問題点を全て修正すると、先に弊社が提案したPMHF式と一致することを示します。提案するPMHF式を使用することでPMHF値の過剰見積もりを防ぐことができます。従ってこのアプローチにより、自動運転に代表される高信頼システムの設計がより容易になることが期待されます。

質問は2件ありましたが、ほぼ同一内容でした。

Q: マルコフ連鎖状態遷移は時間依存であるのに、なぜPMHFは定数なのか？

A: マルコフ連鎖状態遷移で確率微分方程式を建てると、ご質問のように時間依存の関数となります。これは確率密度関数であり、具体的には修理を考慮した、我々の用語でいう不稼働確率密度です。これは定数として扱うことができる故障率と異なり時間依存の関数です。規格はこれについて車両寿命間の平均を取り、PMHFとして定数として扱います。

前のブログ 次のブログ