今までの結果を数式にまとめます。ORゲートまで戻るとLFの項にlatent確率、detected/percieved確率の2つだけでなく、3つ目としてサブツリー確率の和となっています。同様なので本記事では省略しますが、サブツリーの内容はアラームのフォールトとなっています。検出機構だけでなくアラームも2nd SMの一部であるため、LFとして同様に、検出部分と非検出部分に分解して加算するのが正しい方法です。
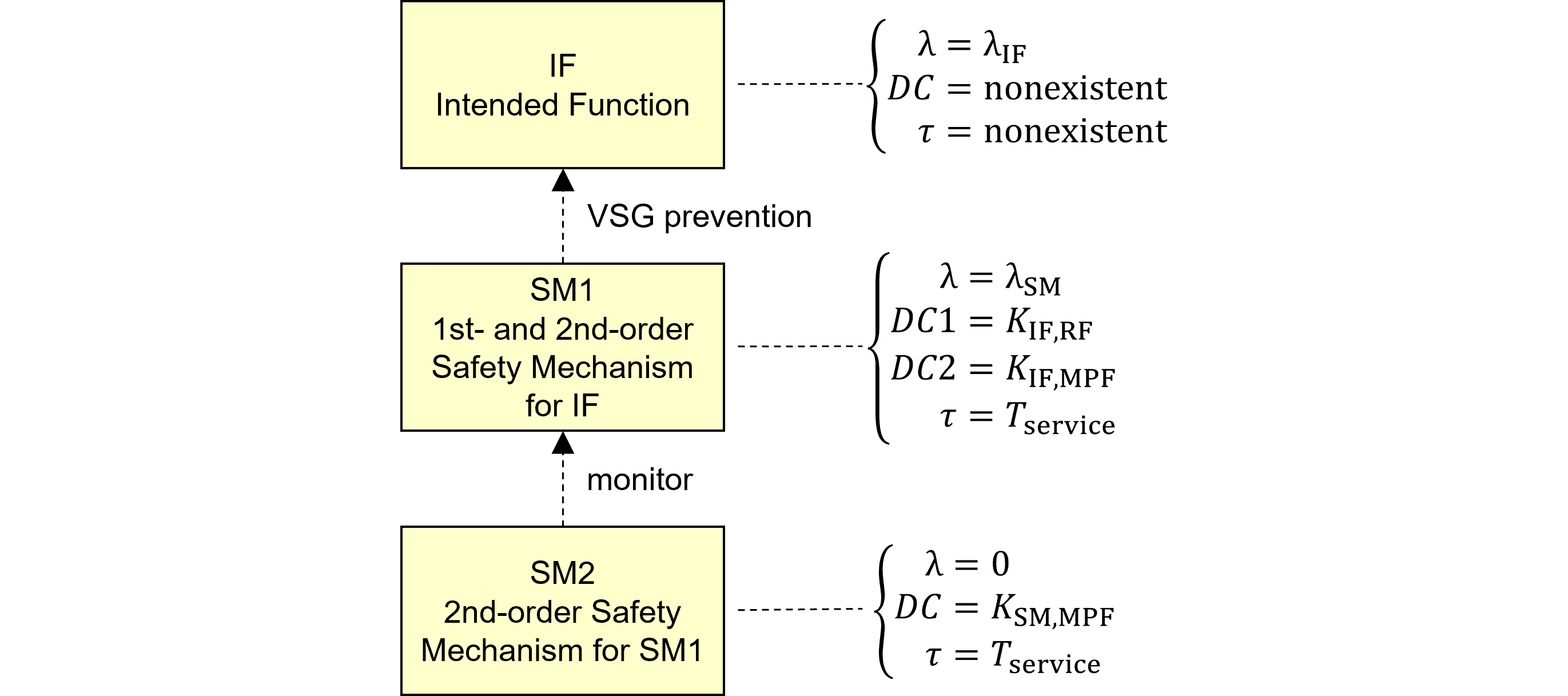
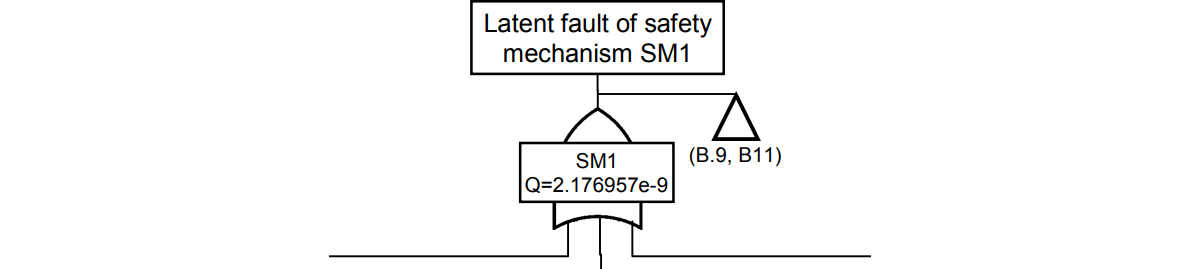 図590.1 規格1st editionのFTA図構成
図590.1 規格1st editionのFTA図構成
今までの式をまとめると、確率は、
$$
Q=\lambda_\text{IF}T_\text{lifetime}\left[(1-DC_\text{1})+\left\{\lambda_\text{SM1}T_\text{lifetime}(1-DC_\text{2})+\frac{1}{2}\lambda_\text{SM1}\tau DC_\text{2}\right\}\cdot DC_\text{1}\right]\tag{590.1}
$$
これを時間平均したものがPMHFなので$T_\text{lifetime}$で割れば、
$$
\require{color}
\definecolor{pink}{rgb}{1.0,0.8,1.0}
M_\text{PMHF}=(1-DC_\text{1})\lambda_\text{IF}+DC_\text{1}\lambda_\text{IF}\left[(1-DC_\text{2})\lambda_\text{SM1}T_\text{lifetime}+\frac{1}{2}DC_\text{2}\lambda_\text{SM1}\tau\right]
\tag{590.2}
$$
ここで、
$$
\begin{eqnarray}
\left\{
\begin{array}{l}
(1-DC_\text{1})\lambda_\text{IF}&=&\lambda_\text{RF}\\
DC_\text{1}\lambda_\text{IF}&=&\lambda_\text{IF,MPF}\\
(1-DC_\text{2})\lambda_\text{SM1}&=&\lambda_\text{SM1,MPF,lat}\\
DC_\text{2}\lambda_\text{SM1}&=&\lambda_\text{SM1,MPF,dp}
\end{array}
\right.\\
\end{eqnarray}
\tag{590.3}
$$
であることを用いれば、
$$
M_\text{PMHF}=\lambda_\text{RF}+\frac{1}{2}\lambda_\text{IF,MPF}(\colorbox{pink}{2}\lambda_\text{SM1,MPF,lat}T_\text{lifetime}+\lambda_\text{SM1,MPF,dp}\tau)
\tag{590.4}
$$
とまとめられるものの、レイテントフォールトの係数が誤っているように思います。RWBの調査をしなければ不明ですが、ミッションタイムを手入力したときのみ$\frac{1}{2}$を掛ける仕様なのでしょうか。もしそうならレイテントの場合だけは、$\frac{1}{2}T_\text{lifetime}$を手入力する必要があります。
正しくは、フォールト順序がSM1⇒IFの場合には、(590.4)のピンクで示した"2"を削除した、
$$
M_\text{PMHF}=\lambda_\text{RF}+\frac{1}{2}\lambda_\text{IF,MPF}(\lambda_\text{SM1,MPF,lat}T_\text{lifetime}+\lambda_\text{SM1,MPF,dp}\tau)
\tag{590.5}
$$
となります。このようにマニュアルで木構造を構築するのはかなり大変なので、ツールにPMHFモデルが組み込まれることが望まれます。
 前のブログ
次のブログ
前のブログ
次のブログ