同じ記事のPMHFについても怪しいところがあります。

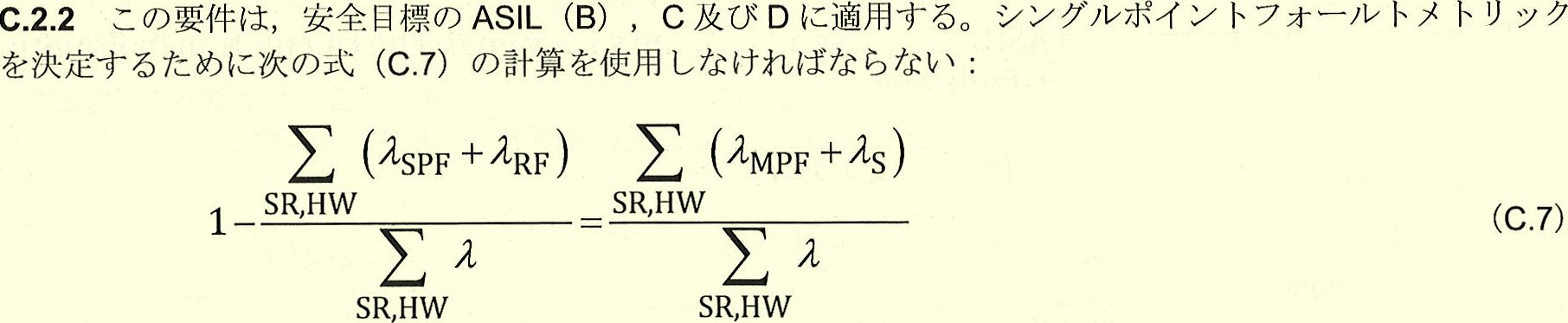
まずPMHFそのものは単純で故障する頻度そのものである。ただ実際には1億回あたり1回未満というのはかなり難しい。一般にエレクトロニクス業界で使われている故障頻度には「FIT」（Failure in Time：10億時間あたりに発生する故障回数）と呼ばれるものがあるが、自動車向けのMCUなどではどんなに少ないものでも20FIT（10億時間あたり20回）といわれており、このままでは10^-8/hを満たせない。 ただ、PMHFは、ある特定の回路そのものの故障頻度ではなく、システム全体の故障頻度と見なすこともできる。例えば全ての部品を二重化しておき、片方が壊れてももう片方がそれを引き継ぐことができるとすれば、トータルとしての故障頻度は10FITに減る計算になり、これでASIL DのPFHFの目標をクリアできることになるからだ。

要約すれば、主系とバックアップ系が、それぞれ20FITの故障率を持つ2重化システムがあるとき、「トータルとしての故障頻度」が10FITになるということのようです。

実際には「トータルとしての故障頻度」はDPF(Dual Point Failure)の時であるから、車両寿命を$T_\text{lifetime}$として単純な確率計算では、 $$ \Pr\{\text{DPF}\}=\Pr\{\text{Channel 1 failed}\cap\text{Channel 2 failed}\} =\Pr\{\text{Channel 1 failed}\}\Pr\{\text{Channel 2 failed}\}\\ =(\lambda_\text{IF}T_\text{lifetime})(\lambda_\text{SM}T_\text{lifetime}) =(10\times 10^{-9})^2{T_\text{lifetime}}^2=1\times 10^{-16}{T_\text{lifetime}}^2 $$ となります。

この確率には主系⇒バックアップ系のフェイルオーバーだけでなく、その逆の場合も含まれるので、フェイルオーバーの場合のPMHF、すなわち平均PUDを求めると、この1/2を$T_\text{lifetime}$で割った値となります。 $$ M_\text{PMHF}=\overline{PUD}=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime} $$

この値は、車両寿命がいくら大きくても10FITにはなりません。例えば車両寿命が10万時間の場合のPMHF、すなわち平均PUDは、 $$ M_\text{PMHF}=\overline{PUD}=\frac{1}{2}\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}=0.5\times 10^{-16}\cdot 1\times 10^{5}=0.005[FIT] $$ となります。逆にこれが10FITだとすると、車両寿命は5,708年というあり得ない値となってしまいます。

誤りの原因は2重化の場合の確率計算を1/2にしてしまったところにあります。本来は2重化システムにおいては、主系に故障があっても、バックアップ系が動作するフォールトトレラント性があるため、引き続いてバックアップ系にもフォールトが起きないとシステムの故障とはなりません。従って、確率計算としては両方にフォールトが起こる場合の、確率の掛け算になります。

以前の記事のように、レアイベント近似を用いれば、直列系は確率の足し算、並列系は確率の掛け算となります。表記の記事は、並列系で確率の掛け算をするところを、2冗長だから単純に1/2をかけたのかもしれませんが、正しくは10[FIT]ではなく0.005[FIT]のような、非常に低い数字になります。

いずれにせよ、故障頻度は故障確率として計算することを理解していないと、このような誤りを引き起こします。

前のブログ 次のブログ

ある記事に以下のような文章が載っていました。SPFM、LFMに関する説明文のようです。

冗長によるPMHFの低減を説明した後に、

　ただこの二重化の場合、ある部品が壊れたかどうかを確認するための仕組みが別途必要になる。また、この仕組みが確実に「その部品が壊れたかどうか」を判断できなければならない。これに関する数値がSPFMであって、要するに99％以上の確率で、その部品が正常か壊れたかを判断できるようにする必要があるわけだ。

　また、この「部品が壊れたかどうか」を判断する回路も、当然電子回路で構成される以上故障する可能性がある。そこで、この判断部そのものが故障していないかどうか、を90％以上の確率で判断できないといけない、というのがLFMというわけだ。

一見良さそうなこの説明文ですが、良く読むと誤りがあります。どこをどう直したら正しくなるか考えてみてください。

• ヒント1: 二重化(冗長)の場合は互いに主機能と安全機構(1st SM)の働きを行います。
• ヒント2: SPFMはこの場合、平均的な故障検出率ではありません。安全機構(1st SM)の持つ平均的な故障抑止率です。二重化は故障を検出しないにも関わらず、VSGを抑止するので、SPFMはほぼ100%となります。
• ヒント3: LFMの対象は「部品が壊れたかどうか」を判断する回路(=故障検出回路)だけではありません。この場合は故障抑止回路(=1st SM)とするべきです。LFMは2nd SMの持つ平均的な故障検出率です。

2とおりの修正方法があります。引用した文章は2つに分かれており、それぞれSPFMとLFMについての説明とするならば、

　ただこの二重化の場合、ある部品が壊れたかどうかを確認するための仕組みが別途必要にならない。また、故障のSG侵害を抑止できなければならない。故障を抑止するカバレージに関する数値がSPFMであって、要するに99％以上の確率で、故障のSG侵害を抑止する必要がある。

　また、この故障がSG侵害を抑止する回路も、当然電子回路で構成される以上故障する可能性がある。そこで、この故障がSG侵害を抑止する回路そのものが故障していないかどうか、を90％以上の確率で判断できないといけない、というのがLFMというわけだ。

となります。あるいは、それぞれLFMと2nd SMの故障検出についての説明とするならば、

　ただこの二重化の場合、ある部品が壊れたかどうかを確認するための仕組みが別途必要になる。また、この仕組みが確実に「その部品が壊れたかどうか」を判断できなければならない。これに関する数値がLFMであって、要するに90％以上の確率で、その部品が正常か壊れたかを判断できるようにする必要があるわけだ。

　また、この「部品が壊れたかどうか」を判断する回路(2nd SM)も、当然電子回路で構成される以上故障する可能性は無い

となります。当然筆者は前者を意図したのでしょうが、文章を大幅に修正しなければなりません。その理由は、元の文章が1st SMの機能である故障抑止と故障検出について混同しているためです。

端的に言えば、著者は「部品の故障を検出する回路(だけ)がSMである」と思い込んでいます。最初から「二重化」で始めなければ、おおむね合っていたのですが。

前のブログ 次のブログ

LFMの導出

LFM、$M_{\mathrm{LFM}}$に関する規格式を引用し、これを導出します。

前稿と同様な論証を行います。まずレイテントフォールト(LF)の故障率の計算式を見てみます。

故障分類フローで説明したように、レイテントフォールトとなるのは2とおり存在します。

• 主機能のフォールトのSG侵害が1st SMにより抑止されている場合に、2nd SMで検出できない場合
• SMのフォールト(これはSG侵害が起こらない)が2nd SMで検出できない場合

よって、安全関連に関する故障モードが$n$個ある場合に、i番目のLFの故障率$\lambda_{\mathrm{LF,}i}$の定義式は、存在しない$\lambda_i$に対しては0を返すものとすれば、

$$ \lambda_{\mathrm{LF,}i}:=DC_i\lambda_{\mathrm{IF,}i}(1-DC2_i)+\lambda_{\mathrm{SM,}i}(1-DC2_i)=\{DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i}\}(1-DC2_i), \\ i=1, 2, ..., n\tag{123.1} $$ と表せます。この$DC2_i$はKパラメータで書けば、 $$ DC2_i=K_{\mathrm{IF,FMC,MPF,}i}, もしくは K_{\mathrm{SM,FMC,MPF,}i} $$ で、2nd SMがIFもしくはSMに対して、故障検出する割合を表します。(123.1)の両辺の総和を取れば、 $$ \sum_{i=1}^n\lambda_{\mathrm{LF,}i}=\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})(1-DC2_i)\\ =\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i \tag{123.2} $$ よって、$\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})$及び$\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i$を移項し、 $$ \sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i=\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n\lambda_{\mathrm{LF,}i} \tag{123.3} $$ ここで、DC2の、各々の故障率による加重平均を(123.4)のように定義し、(123.3)を(123.4)の分子に代入すれば、 $$ \overline{DC2}:=\frac{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})DC2_i}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})} =\frac{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})-\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})}\\ =1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(DC_i\lambda_{\mathrm{IF,}i}+\lambda_{\mathrm{SM,}i})} \tag{123.4} $$ ここで、$DC_i\lambda_{\mathrm{IF,}i}=\lambda_{\mathrm{IF,}i}-\lambda_{\mathrm{RF,}i}$を代入すれば、(123.4)は $$ (123.4)=1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(\lambda_{\mathrm{IF,}i}-\lambda_{\mathrm{RF,}i}+\lambda_{\mathrm{SM,}i})}=1-\frac{\sum_{i=1}^n\lambda_{\mathrm{LF,}i}}{\sum_{i=1}^n(\lambda_i-\lambda_{\mathrm{RF,}i})}\tag{123.5} $$

これと(C.8)を比較すれば、$\img[-1.35em]{/images/withinseminar.png}$

前のブログ 次のブログ

SPFMの導出

SPFM、$M_{\mathrm{SPFM}}$に関する規格式を引用し、これを導出します。

まずレシデュアルフォールト(RF)の故障率の計算式を見てみます。ここでシングルポイントフォールト(SPF)を狭義に使えば、RFのうち、ダイアグノスティックカバレージ(DC)がゼロの時にSPFと等価であるため、SPFもRFも(広義の)RFとして表せることになります。つまり上式分子の$\lambda_{\mathrm{SPF}}+\lambda_{\mathrm{RF}}$は、DC=0の場合を含み、$\lambda_{\mathrm{RF}}$と簡単化できます。

さて、安全関連に関する故障モードが$n$個ある場合に、i番目の(広義の)RFの故障率$\lambda_{\mathrm{RF,}i}$式は、 $$ \lambda_{\mathrm{RF,}i}:=\lambda_{\mathrm{IF,}i}(1-DC_{i})\tag{122.1} $$ と定義されます。この$DC_i$はKパラメータで書けば、 $$ DC_i=K_{\mathrm{IF,FMC,RF,}i} $$ となり、1st SMがIFに対して、IFがSG侵害を抑止する割合を表します。(122.1)の両辺の総和を取れば、 $$ \sum_{i=1}^n\lambda_{\mathrm{RF,}i}=\sum_{i=1}^n\lambda_{\mathrm{IF,}i}(1-DC_{i}) =\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_{i} \tag{122.2} $$ よって、 $$ \sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_{i}=\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{RF,}i} \tag{122.3} $$ ここで、各々のSMにより防御される、IFの故障率によるDCの加重平均を次のように定義し、 $$ \overline{DC}:=\frac{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}DC_i}{\sum_{i=1}^n\lambda_i} \tag{122.4} $$ (122.3)を(122.4)の分子に代入すれば、 $$ (122.4)=\frac{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}-\sum_{i=1}^n\lambda_{\mathrm{RF,}i}}{\sum_{i=1}^n\lambda_{\mathrm{IF,}i}} =1-\frac{\sum_{i=1}^n\lambda_{\mathrm{RF,}i}}{\sum_{i=1}^n\lambda_i} \tag{122.4} $$ これと(C.7)を比較すれば、 $$ M_{\mathrm{SPFM}}=\overline{DC} $$ となるため、SPFMは$\img[-1.35em]{/images/withinseminar.png}$

前のブログ 次のブログ

車両寿命間のダウン確率は、次の式のようにPMHFに車両寿命をかけたものです。 $$ M_\mathrm{PMHF}:=\frac{1}{T_\mathrm{lifetime}}\Pr\{\text{item down at }T_\mathrm{lifetime}\}\\ \therefore \Pr\{\text{item down at }T_\mathrm{lifetime}\}=M_\mathrm{PMHF}T_\mathrm{lifetime} \tag{121.1} $$ バックアップ系(SM1)に切り替わった後で、EOTTI期間走行する間のダウン確率が(121.1)以下であればよいとすれば、 $$ \Pr\{\text{backup down at }T_\mathrm{eotti}\}=\lambda_\mathrm{SM1, DPF}T_\mathrm{eotti}\le\Pr\{\text{item down at }T_\mathrm{lifetime}\}=M_\mathrm{PMHF}T_\mathrm{lifetime}\tag{121.2} $$ となり、EOTTIの範囲は前稿の規格式(3)で表されます。しかしながら、恐らくワーストケース(最短EOTTI)を求めるための条件と思われますが、厳しすぎに見えます。$t=0$でIFのフォールトが起きた前提での、バックアップ系による走行条件の計算となっています。DPFの確率ではなく、SPFの確率となるため、何桁も厳しくなります。

次に規格式(2)ですが、誤ったPMHF式がベースであるため、以下の例では誤ったEOTTIが得られています。表121.1でケース2の「(2)式の結果」が、上記のワーストと思われる「(3)式の結果」を下回っている(より厳しくなっている)こともこれを裏付けます。

まず正しいEOTTI式を(121.3)に示します。これは、2nd Editionの条件(IF/SM1共にリペアラブル)を前提としてPMHF式を求め(69.1)、その暴露時間の最大値をEOTTIとし、EOTTIについて解いた式です。 $$ T_\text{eotti}\le\frac{M_\text{PMHF}-\left[\lambda_\text{SPF}+\lambda_\text{RF}+\lambda_\text{IF,DPF}\lambda_\text{SM,DPF}(1-K_\text{MPF})T_\text{lifetime}\right]}{\lambda_\text{IF,DPF}\lambda_\text{SM,DPF}K_\text{MPF}}\\ =\frac{M_\text{PMHF}-\left[\lambda_\text{SPF}+\lambda_\text{RF}+\lambda_\text{IF,DPF}\lambda_\text{SM,DPF}(1-K_\text{IF,MPF})(1-K_\text{SM,MPF})T_\text{lifetime}\right]}{\lambda_\text{IF,DPF}\lambda_\text{SM,DPF}\left[1-(1-K_\text{IF,MPF})(1-K_\text{SM,MPF})\right]}\\ =\frac{M_\text{PMHF}-(\lambda_\text{SPF}+\lambda_\text{RF}+\lambda_\text{IF,DPF,lat}\lambda_\text{SM,DPF,lat}T_\text{lifetime})}{\lambda_\text{IF,DPF}\lambda_\text{SM,DPF}-\lambda_\text{IF,DPF,lat}\lambda_\text{SM,DPF,lat}} \tag{121.3} $$ 次に規格中の例題を(121.3)で計算し直した結果、表121.1の最下段のようになります。

規格の2例で総合的な$K_\text{MPF}$を求めると、ケース1, 2において0.99と変わりませんが、これを振ってみた、$T_\text{eotti}$に関するグラフを図121.3に示します。(121.3)が不等式であるため、解の存在領域は曲線の下側となります。

ケース2では、本来965Hで良いのに31Hと厳しくなっているので、

規格によれば、ダウン率の過大評価に基づく、EOTTIの31.3倍の過小評価をしていると結論づけます。

まとめると、フォールトトレラントシステムのマルコフ連鎖を考えると、(3)は過小評価しすぎと考えます。その理由は、ワーストケースとはいえ、ダウン率の高いSM1(バックアップ系)のみでEOTTI時間動作することを想定していますが、実際にはダウン率の低い主機能との組み合わせで動作するためです。本来のPMHF式(68.1)や(98.7)に示す$T_\mathrm{service}$を$T_\mathrm{eotti}$に置き換えた式が正しいと考えます。

いずれにしろ、規格2nd Editionで(3)を使用しているのは、EOTTIを過小評価しすぎです、(2)は誤って過小評価しているためあまり目立たなくなっていますが、本来(2)の制約のみで良いと考えます。しかしながら(2)式が誤っているので、(68.1)や(98.7)を使用すべきです。

この結果はRAMS2020で発表しました。

前のブログ 次のブログ