|
16 |
PMHF導出法の変更 (5) |
よって、MPF detectedを考慮した場合のPMHFは、それぞれの事象は排他であることから、(361.5)、(362.6)、(363.4)で求められた平均PUDを全て加えることで求められ、 $$ \begin{eqnarray} \require{cancel} M_\text{PMHF}&=&\overline{q_\mathrm{SPF,IFU}}+\overline{q_\mathrm{DPF1,IFR}}+\overline{q_\mathrm{DPF2, IFR}}\\ &=&(1-K_\text{IF,RF})\lambda_\text{IF}-\bcancel{(1-K_\text{IF,RF})\alpha}+\bcancel{(1-K_\text{IF,RF})\alpha}+K_\text{IF,RF}\color{red}{K_\text{IF,det}}\alpha\\ & &+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta+K_\text{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta\\ &=&\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\color{red}{K_\text{IF,det}}\alpha+2K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}\beta}\\ &=&(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_\text{IF,RF}\color{red}{K_\text{IF,det}}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau]\\ & &+K_\mathrm{IF,RF}\color{red}{(1-K_\text{IF,det})}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau],\\ \end{eqnarray}\tag{364.1} $$
$$ ただし、\begin{cases} \begin{eqnarray} \alpha&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau]\\ \beta&:=&\frac{1}{2}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_{\mathrm{MPF}})T_\text{lifetime}+K_{\mathrm{MPF}}\tau]\\ K_{\mathrm{MPF}}&:=&K_{\mathrm{IF,MPF}}+K_{\mathrm{SM,MPF}}-K_{\mathrm{IF,MPF}}K_{\mathrm{SM,MPF}} \end{eqnarray} \end{cases} $$ この一般式に対して場合分けを行って、
非冗長系においては抑止されるフォールトは全て検出可能なので、$K_\text{IF,det}=1$とすれば、 $$ M_\text{PMHF,NRD}=\bbox[#ccffff,2pt]{(1-K_\text{IF,RF})\lambda_\text{IF}+K_\text{IF,RF}\alpha}\\ =(1-K_\text{IF,RF})\lambda_\text{IF}+\frac{1}{2}K_\text{IF,RF}\lambda_{\mathrm{IF}}\lambda_{\mathrm{SM}}[(1-K_\mathrm{SM,MPF})T_\text{lifetime}+K_\mathrm{SM,MPF}\tau] \tag{364.2} $$
冗長系においては抑止されるフォールトは(1st SMでは)全て検出不可であり、一方全て抑止されるため、$K_\text{IF,det}=0, K_\text{IF,RF}=1$とすれば、 $$ M_\text{PMHF,RD}=\bbox[#ccffff,2pt]{2\beta}=\lambda_\mathrm{IF}\lambda_\mathrm{SM}[(1-K_\mathrm{MPF})T_\text{lifetime}+K_\mathrm{MPF}\tau] \tag{364.3} $$ このように、非冗長系と冗長系に対するPMHF式が導出されます。
非冗長系1.の(364.2)は、規格第1版PMHF第1式と完全に一致しています。
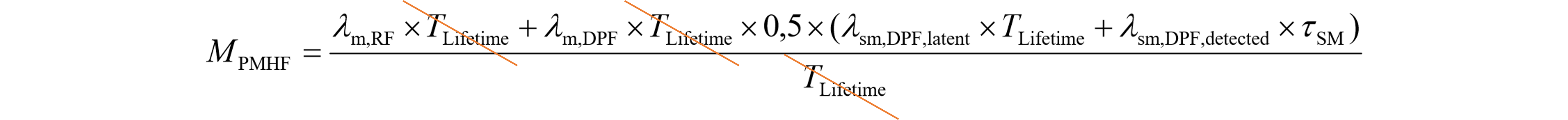
その理由は、規格第1版の前提がIFUモデルだからであり、IFのレイテントフォールトが無い場合、つまりIFの検出されたフォールトは全て即時修理されるモデルだからです。従って、冗長系に適用できないのは当然であり、論文の必然性があったわけです。
RAMS 2022においてMPF detectedの再考に基づくPMHF式の論文発表が終了したため、秘匿部分を開示します。

Leave a Comment