|
6 |
規格第2版のPMHF式の疑問 (15) |
ここまでで規格解説書方式と弊社CTMCベースでは積分順序に違いがあることがわかります。パターン1はフォールトの生起はSM1⇒IFの順であり、かつSM1のフォールトはSM2により検出されず、全量レイテントとなる場合です。表479.1に示すように規格解説書の方式は、積分順序がフォールト生起とは逆順です。
| パターン1 | フォールト 生起順序 |
積分順序 |
|---|---|---|
| 規格解説書方式 | SM1⇒IF | IF⇒SM1 |
| 弊社CTMC方式 | SM1⇒IF | |
規格解説書方式
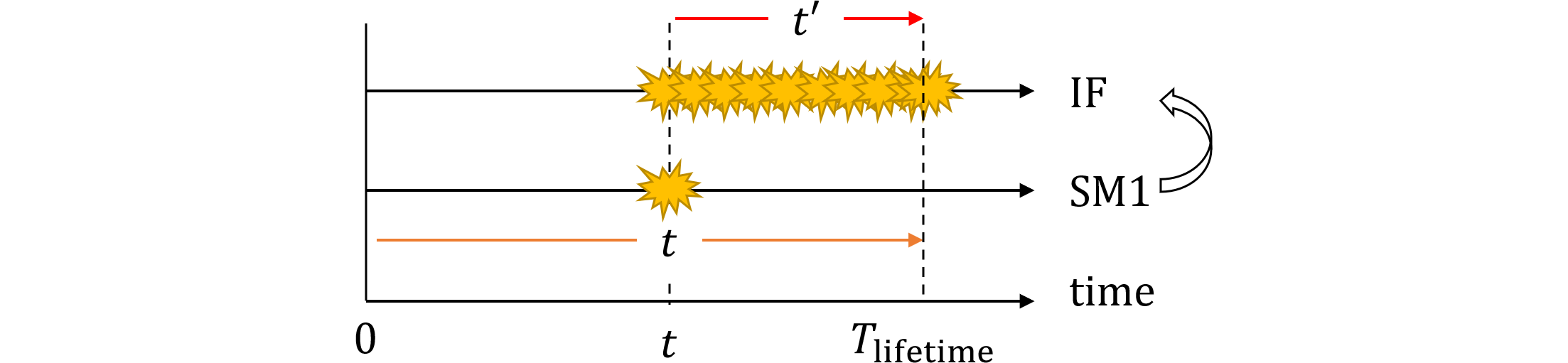
規格解説書によればPoF(Probability of Failure)は、 $$ PoF_\text{SM1,lat⇒IF}=\int_0^{T_\text{lifetime}}f_\text{SM1,DPF,lat}(t)\left[\int_t^{T_\text{lifetime}}f_\text{IF,DPF}(t')dt'\cdot R_\text{IF}(t)\right]dt \tag{479.1} $$ と記載されています。その意味は図479.1で示すように、時刻$t$から車両寿命まで、後フォールトであるIFに関する積分を先に実行し、後から先フォールトであるSM1の積分を実行しています。
第1の誤り
(479.3)は[]内のIFについての積分に2か所誤りが有ります。まず、「IFが時刻$t$までup」という条件 $R_\text{IF}(t)$がかけられていますが、IFのフォールト時刻は図479.1より時刻$t'$であるため、IFは$t'$までupでなければなりません。従って、 $$R_\text{IF}(t)⇒R_\text{IF}(t')$$ と修正します。
$R_\text{IF}(t)$を用いることもできますが、さらに「IFが時刻$t$までupという条件下で時刻$t'$までup」という条件付き確率をかける必要があります。そうしないと時刻$t$から$t'$までの変化を無視してしまいます。条件付き確率の公式 $$ \Pr\{A|B\}=\frac{\Pr\{A\cap B\}}{\Pr\{B\}} $$ を用れば、 $$ \require{cancel} \Pr\{\text{IF up at }t\}\cdot\Pr\{\text{IF up at t'}|\text{IF up at }t\}=\bcancel{R_\text{IF}(t)}\cdot \frac{R_\text{IF}(t')}{\bcancel{R_\text{IF}(t)}}=R_\text{IF}(t’) $$ となり、前述のように$R_\text{IF}(t)$⇒$R_\text{IF}(t')$と修正したのと同じことになります。
第2の誤り
2点目は$f_\text{IF}(t')$が誤りです。IFのupとdownの事象は独立ではないので、これは「IFが時刻$t'$までupという条件下で$t'$から$t'+dt'$までの間にIFがフォールトする」という条件付き確率でなければなりません。 そのため、(66.4)の確率密度関数ではなく(66.8)の故障率をかける必要があります。従って、 $$ f_\text{IF}(t')dt'⇒\lambda_\text{IF}dt' $$ と修正します。
パターン1のPMHFの導出
上記の誤り2点を修正すれば(479.3)は、 $$ M_\text{PMHF,com,P1}=\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF}) \int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[\int_t^{T_\text{lifetime}}R_\text{IF}(\color{red}{t'})\cdot\color{red}{\lambda_\text{IF}}dt'\right]dt\\ =\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF}) \int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[\int_t^{T_\text{lifetime}}f_\text{IF}(t')dt'\right]dt\\ =\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF}) \int_0^{T_\text{lifetime}}f_\text{SM1}(t)\left[F_\text{IF}(T_\text{lifetime})-F_\text{IF}(t)\right]dt\\ =\frac{K_\text{IF,DPF}}{T_\text{lifetime}}(1-K_\text{SM1,DPF})\left[F_\text{IF}(T_\text{lifetime})F_\text{SM}(T_\text{lifetime})- \int_0^{T_\text{lifetime}}f_\text{SM1}(t)F_\text{IF}(t)dt\right]\quad\quad\color{red}{※}\\ \approx K_\text{IF,DPF}(1-K_\text{SM1,DPF})\left[\lambda_\text{IF}\lambda_\text{SM}T_\text{lifetime}- \frac{1}{T_\text{lifetime}}\int_0^{T_\text{lifetime}}f_\text{SM1}(t)F_\text{IF}(t)dt\right]\\ =\img[-1.35em]{/images/withinseminar.png} \tag{479.4} $$ と求められます。導出には公式(60.6)を使用しました。
若干気持ち悪いのは、フォールト順がSM1⇒IFであるのに対して、積分順序が逆順になっていることです。(479.4)$\color{red}{※}$行を見ても、SM1⇒IFの確率を求めるのにあたり、DPF確率全体$F_\text{IF}(T_\text{lifetime})F_\text{SM}(T_\text{lifetime})$から逆順であるIF⇒SM1の確率を引いており、straight forwardではありません。
本稿では上記2点の誤りを修正しましたが、結果として解説書の方式でも結果は変わりません。従って、これらはマイナーな誤りと判定します。
なお、本稿はRAMS 2024に投稿予定のため一部を秘匿していますが、論文公開後の2024年2月頃に開示予定です。

Leave a Comment