|
16 |
アイテムの故障率 (2) |
並列アイテム
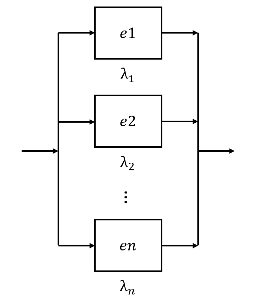
並列アイテムとは、上図のように、RBDを書いたときにアイテムを構成するエレメントが並列になっている場合のアイテムです。この場合(1 out of n)は冗長性を持っており、全てのエレメントが故障しなければ、アイテムは故障しません。
このように、信頼度から考えると冗長が良いに決まっているのですが、2冗長でもコストが倍増することになります。従って、いかに冗長のコストを抑えるかが、良い設計の鍵となります。
この場合並列アイテムの信頼度は各エレメントの信頼度の和、と単純にはなりません。その理由は、各事象の確率の和が和事象の確率になるのは、各事象が排他の場合のみであることです。一般に各事象は独立であっても排他ではありません。
例えばエレメント1とエレメント2が99%の信頼度だとすれば、信頼度を加え合わせると0.99+0.99=1.98の確率というわけのわからない数字となります。言うまでもなく、確率は0から1の間の値の値を取るはずです。これはエレメント1とエレメント2が共に動作している確率のダブルカウントが原因なので、先の確率の和である1.98から同時に動作している確率0.99*0.99を引くと並列アイテムの信頼性が求められ、1.98-0.99*0.99=0.9999、99.99%となります。
これを一般化し、並列アイテムの信頼度は包除原理から、 \[ R_{item}(t)=\coprod_{i=1}^n R_i(t)=\sum_{i=1}^n R_i(t)-\sum_{i\lt j}^n R_i(t)\cdot R_j(t)+\cdots+(-1)^{n-1}\prod_{i=1}^n R_i(t)\tag{9.1} \]
のように複雑な式となるため、アイテムの不信頼度を考えたほうが楽です。すると、並列アイテムの不信頼度は全てのエレメントの不信頼度の積となるため、
並列アイテムの不信頼度の式: \[ F_{item}(t)=F_1(t)\cdot F_2(t)\cdot\cdots\cdot F_n(t)=\prod_{i=1}^n F_i(t)\tag{9.2} \]
であり、これはFTAの計算時に使用するため重要な式となります。
以降では教科書的に信頼性を求めることにし、(9.2)を信頼度で表わせば、 \[ F_{item}(t)=1-R_{item}(t)=\prod_{i=1}^n[1-R_i(t)]\tag{9.3} \]
従って並列アイテムの信頼度は各エレメントの故障率で表すことができ、 \[ R_{item}(t)=1-\prod_{i=1}^n[1-R_i(t)]=1-\prod_{i=1}^n(1-e^{-\lambda t})\tag{9.4} \]
となります。
