直列アイテム

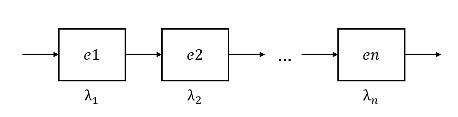
直列アイテムとは、上図のように、RBD(信頼性ブロック図)を書いたときにアイテムを構成するエレメントが直列になっている場合のアイテムです。この場合は冗長性を持たないため、どのひとつのエレメントが故障しても、それによりアイテムが故障すると考えます。この場合のアイテムの信頼度は各エレメントの信頼度の積となります。 \[ R_{item}(t)=R_1(t)\cdot R_2(t)\cdot\cdots\cdot R_n(t)=\prod_{i=1}^n R_i(t)\tag{8.1} \]

ここで、信頼度を故障率で表す(4.2)を用いれば、(8.2)となります。 \[ R_{item}(t)=e^{-\lambda_{item}t}=e^{-\lambda_1 t}\cdot e^{-\lambda_2 t}\cdot\cdots\cdot e^{-\lambda_n t} =e^{\sum_{i=1}^n-\lambda_i t}\tag{8.2} \]

従って、アイテムの故障率は(8.3)のように各エレメントの故障率の和で求められます。 \[ \therefore\lambda_{item}=\sum_{i=1}^n \lambda_i\tag{8.3} \]

教科書には何故か信頼度の式しか出てこないようですが、後でFTAの計算を行うときに不信頼度が重要となるため、ここで掲載しておきます。(8.1)に(2.5)を代入して、以下の(8.4)が得られます。

直列アイテムの不信頼度の式： \[ F_{item}(t)=1-\prod_{i=1}^n[1-F_i(t)]\tag{8.4} \]

前のブログ 次のブログ